題目列表(包括答案和解析)
已知數(shù)列{
}是等差數(shù)列，且滿足：a1＋a2＋a3＝6，a5＝5；
數(shù)列{
}滿足：－
＝
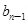（n≥2，n∈N﹡），b1＝1．
（Ⅰ）求和；
（Ⅱ）記數(shù)列
＝
（n∈N﹡），若{}的前n項和為
，求.
已知數(shù)列{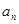
}是等差數(shù)列，且滿足：a1＋a2＋a3＝6，a5＝5；
數(shù)列{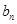
}滿足：－
＝
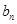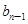（n≥2，n∈N﹡），b1＝1．
（Ⅰ）求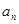和；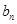
（Ⅱ）記數(shù)列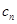
＝
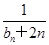（n∈N﹡），若{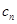}的前n項和為
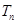，求.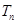
（本小題滿分12分）
已知數(shù)列{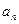
}的前n項和
＝2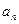－，數(shù)列{
}滿足b1＝1， b3＋b7＝18，且
＋
＝2（n≥2）．
（Ⅰ）求數(shù)列{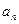}和{}的通項公式；
（Ⅱ）若
＝
，求數(shù)列{}的前n項和
．
已知{an}是正數(shù)組成的數(shù)列，a1＝1，且點(，an+1)(n∈N*）在函數(shù)y＝x2＋1的圖象上.(Ⅰ)求數(shù)列｛an｝的通項公式；(Ⅱ)若列數(shù)｛bn｝滿足b1＝1,bn+1＝bn＋2an，求證：bn ·bn+2＜b2n+1.
已知數(shù)列{an}的前n項和為Sn，設an是Sn與2的等差中項，數(shù)列{bn}中，b1＝1，bn＋1＝bn＋2.
(1)求an，bn；
(2)若數(shù)列{bn}的前n項和為Bn，比較
＋
＋…＋
與2的大小；
(3)令Tn＝
＋
＋…＋
，是否存在正整數(shù)M，使得Tn<M對一切正整數(shù)n都成立？若存在，求出M的最小值；若不存在，請說明理由．
一、選擇題（每小題5分，共60分）
1－12BDCBC CCDBA AC
二、填空題（每題4分，共16分）
13、
14、
15、1 16、15
三、解答題（共74分）
17、（本小題滿分12分）
（1）
函數(shù)
的最小正周期是
當
時，即
時，函數(shù)有最大值1。
（2）由
，得
當
時，取
得，函數(shù)的單調遞減區(qū)間是
（3）
18、（本小題滿分12分）
（1）由題意知：
且
，∴
＝1
∵
①，∴當 n≥2時, 
②
①－②得：
∴
∵
＞0，∴
，（n≥2且
）
∴
是以＝1為首項，d＝1為公差的等差數(shù)列
∴＝n
（2）
∴
是以
為首項，
為公比的等比數(shù)列
∴
，∴
，
∴
①
∴
②
①－②得
∴
19、（本小題滿分12分）
（1）當
時，
在
上是增函數(shù)
∴在
上是增函數(shù)
∴當
時，
（2）
在上恒成立
∴
在上恒成立
∴
在上恒成立
在上是減函數(shù)，
∴當
時，
∴
，
∴所求實數(shù)a的取值范圍為
20、（本小題滿分12分）
由
此時
∴
又
，∴
，∴
∴實數(shù)a不存在
21、（本小題滿分12分）
（1）若方程表示圓，則
，∴
（2）設M、N的坐標分別為
、
由
，得
又
，∴
，∴
①
由
，得
∴
代入①得
，
∴
（3）設MN為直徑的圓的方程為
，
即
又
∴所求圓的方程為
22、（本小題滿分14分）
（1）當
時，
設x為其不動點，則
，即
∴
或2，即的不動點是－1，2
（2）由
得
由題意知，此方程恒有兩個相異的實根
∴
對任意的
恒成立
∴
，∴
（3）設
，則直線AB的斜率
，∴
由（2）知AB中點M的坐標為
又∵M在線段AB的垂直平分線
上，∴
∴
（當且僅當
時取等號）
∴實數(shù)b的取值范圍為
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com