題目列表(包括答案和解析)
（本小題滿分12分）
已知p：方程x2＋mx＋1＝0有兩個(gè)不相等的負(fù)實(shí)根；q：不等式4x2＋4(m－2)x＋1＞0的解集為R，若p或q為真命題，p且q為假命題，求m的取值范圍．
（本小題滿分12分）已知⊙C：x2＋y2－2x－2y＋1＝0，直線l與⊙C相切且分別交x軸、y軸正向于A、B兩點(diǎn)，O為坐標(biāo)原點(diǎn)，且
＝a，
＝b（a＞2，b＞2）．
（Ⅰ）求線段AB中點(diǎn)的軌跡方程.
（Ⅱ）求△ABC面積的極小值．
（本小題滿分12分）
已知p：方程x2＋mx＋1＝0有兩個(gè)不等的負(fù)實(shí)根，q：方程4x2＋4(m－2)x＋1＝0無實(shí)根。若p或q 為真，p且q為假。求實(shí)數(shù)m的取值范圍。
（本小題滿分12分）
已知函數(shù)f(x)＝x－ln(x＋a)．（a是常數(shù)）
(I)求函數(shù)f(x)的單調(diào)區(qū)間；
(II) 當(dāng)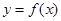
在x＝1處取得極值時(shí)，若關(guān)于x的方程f(x)＋2x＝x2＋b在[，2]上恰有兩個(gè)不相等的實(shí)數(shù)根，求實(shí)數(shù)b的取值范圍；
(III)求證:當(dāng)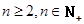
時(shí)
．
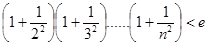（本小題滿分12分）
已知函數(shù)f（x）＝ln（x＋a）－x2－x在x＝0處取得極值．
（Ⅰ）求實(shí)數(shù)a的值；
（Ⅱ）若關(guān)于x的方程f（x）＝－
x＋b在區(qū)間[0，2]上恰有兩個(gè)不同的實(shí)數(shù)根，求實(shí)數(shù)b的取值范圍；
（Ⅲ）證明：對(duì)任意的正整數(shù)n，不等式ln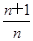
<
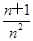都成立．
一、選擇題（每小題5分，共60分）
1－12BDCBC CCDBA AC
二、填空題（每題4分，共16分）
13、
14、
15、1 16、15
三、解答題（共74分）
17、（本小題滿分12分）
（1）
函數(shù)
的最小正周期是
當(dāng)
時(shí)，即
時(shí)，函數(shù)有最大值1。
（2）由
，得
當(dāng)
時(shí)，取
得，函數(shù)的單調(diào)遞減區(qū)間是
（3）
18、（本小題滿分12分）
（1）由題意知：
且
，∴
＝1
∵
①，∴當(dāng) n≥2時(shí), 
②
①－②得：
∴
∵
＞0，∴
，（n≥2且
）
∴
是以＝1為首項(xiàng)，d＝1為公差的等差數(shù)列
∴＝n
（2）
∴
是以
為首項(xiàng)，
為公比的等比數(shù)列
∴
，∴
，
∴
①
∴
②
①－②得
∴
19、（本小題滿分12分）
（1）當(dāng)
時(shí)，
在
上是增函數(shù)
∴在
上是增函數(shù)
∴當(dāng)
時(shí)，
（2）
在上恒成立
∴
在上恒成立
∴
在上恒成立
在上是減函數(shù)，
∴當(dāng)
時(shí)，
∴
，
∴所求實(shí)數(shù)a的取值范圍為
20、（本小題滿分12分）
由
此時(shí)
∴
又
，∴
，∴
∴實(shí)數(shù)a不存在
21、（本小題滿分12分）
（1）若方程表示圓，則
，∴
（2）設(shè)M、N的坐標(biāo)分別為
、
由
，得
又
，∴
，∴
①
由
，得
∴
代入①得
，
∴
（3）設(shè)MN為直徑的圓的方程為
，
即
又
∴所求圓的方程為
22、（本小題滿分14分）
（1）當(dāng)
時(shí)，
設(shè)x為其不動(dòng)點(diǎn)，則
，即
∴
或2，即的不動(dòng)點(diǎn)是－1，2
（2）由
得
由題意知，此方程恒有兩個(gè)相異的實(shí)根
∴
對(duì)任意的
恒成立
∴
，∴
（3）設(shè)
，則直線AB的斜率
，∴
由（2）知AB中點(diǎn)M的坐標(biāo)為
又∵M(jìn)在線段AB的垂直平分線
上，∴
∴
（當(dāng)且僅當(dāng)
時(shí)取等號(hào)）
∴實(shí)數(shù)b的取值范圍為
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com