
題目列表(包括答案和解析)
已知點(diǎn) (
( ),過(guò)點(diǎn)
),過(guò)點(diǎn) 作拋物線(xiàn)
作拋物線(xiàn) 的切線(xiàn),切點(diǎn)分別為
的切線(xiàn),切點(diǎn)分別為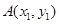 、
、 (其中
(其中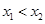 ).
).
(Ⅰ)若 ,求
,求 與
與 的值;
的值;
(Ⅱ)在(Ⅰ)的條件下,若以點(diǎn) 為圓心的圓
為圓心的圓 與直線(xiàn)
與直線(xiàn) 相切,求圓
相切,求圓 的方程;
的方程;
(Ⅲ)若直線(xiàn) 的方程是
的方程是 ,且以點(diǎn)
,且以點(diǎn) 為圓心的圓
為圓心的圓 與直線(xiàn)
與直線(xiàn) 相切,
相切,
求圓 面積的最小值.
面積的最小值.
【解析】本試題主要考查了拋物線(xiàn)的的方程以及性質(zhì)的運(yùn)用。直線(xiàn)與圓的位置關(guān)系的運(yùn)用。
中∵直線(xiàn) 與曲線(xiàn)
與曲線(xiàn) 相切,且過(guò)點(diǎn)
相切,且過(guò)點(diǎn) ,∴
,∴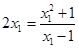 ,利用求根公式得到結(jié)論先求直線(xiàn)
,利用求根公式得到結(jié)論先求直線(xiàn) 的方程,再利用點(diǎn)P到直線(xiàn)的距離為半徑,從而得到圓的方程。
的方程,再利用點(diǎn)P到直線(xiàn)的距離為半徑,從而得到圓的方程。
(3)∵直線(xiàn) 的方程是
的方程是 ,
, ,且以點(diǎn)
,且以點(diǎn) 為圓心的圓
為圓心的圓 與直線(xiàn)
與直線(xiàn) 相切∴點(diǎn)
相切∴點(diǎn) 到直線(xiàn)
到直線(xiàn) 的距離即為圓
的距離即為圓 的半徑,即
的半徑,即 ,借助于函數(shù)的性質(zhì)圓
,借助于函數(shù)的性質(zhì)圓 面積的最小值
面積的最小值
(Ⅰ)由 可得,
可得, . ------1分
. ------1分
∵直線(xiàn) 與曲線(xiàn)
與曲線(xiàn) 相切,且過(guò)點(diǎn)
相切,且過(guò)點(diǎn) ,∴
,∴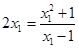 ,即
,即 ,
,
∴ ,或
,或 , --------------------3分
, --------------------3分
同理可得: ,或
,或 ----------------4分
----------------4分
∵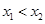 ,∴
,∴ ,
, . -----------------5分
. -----------------5分
(Ⅱ)由(Ⅰ)知, ,
, ,則
,則 的斜率
的斜率 ,
,
∴直線(xiàn) 的方程為:
的方程為: ,又
,又 ,
,
∴ ,即
,即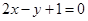 . -----------------7分
. -----------------7分
∵點(diǎn) 到直線(xiàn)
到直線(xiàn) 的距離即為圓
的距離即為圓 的半徑,即
的半徑,即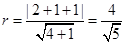 ,--------------8分
,--------------8分
故圓 的面積為
的面積為 . --------------------9分
. --------------------9分
(Ⅲ)∵直線(xiàn) 的方程是
的方程是 ,
, ,且以點(diǎn)
,且以點(diǎn) 為圓心的圓
為圓心的圓 與直線(xiàn)
與直線(xiàn) 相切∴點(diǎn)
相切∴點(diǎn) 到直線(xiàn)
到直線(xiàn) 的距離即為圓
的距離即為圓 的半徑,即
的半徑,即 , ………10分
, ………10分
∴
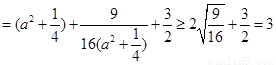 ,
,
當(dāng)且僅當(dāng) ,即
,即 ,
, 時(shí)取等號(hào).
時(shí)取等號(hào).
故圓 面積的最小值
面積的最小值 .
.
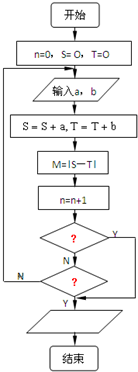 在第十六屆廣州亞運(yùn)會(huì)上,某項(xiàng)目的比賽規(guī)則為:由兩人(記為甲和乙)進(jìn)行比賽,每局勝者得1分,負(fù)者得0分(無(wú)平局),比賽進(jìn)行到有一人比對(duì)方多2分或打滿(mǎn)6局時(shí)停止.設(shè)甲在每局中獲勝的概率為p(p>0.5),且各局勝負(fù)相互獨(dú)立.已知第二局比賽結(jié)束時(shí)比賽停止的概率為
在第十六屆廣州亞運(yùn)會(huì)上,某項(xiàng)目的比賽規(guī)則為:由兩人(記為甲和乙)進(jìn)行比賽,每局勝者得1分,負(fù)者得0分(無(wú)平局),比賽進(jìn)行到有一人比對(duì)方多2分或打滿(mǎn)6局時(shí)停止.設(shè)甲在每局中獲勝的概率為p(p>0.5),且各局勝負(fù)相互獨(dú)立.已知第二局比賽結(jié)束時(shí)比賽停止的概率為| 5 | 9 |
已知 ,(其中
,(其中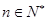 )
)
⑴求 及
及 ;
;
⑵試比較 與
與 的大小,并說(shuō)明理由.
的大小,并說(shuō)明理由.
【解析】第一問(wèn)中取 ,則
,則 ;
…………1分
;
…………1分
對(duì)等式兩邊求導(dǎo),得
取 ,則
,則 得到結(jié)論
得到結(jié)論
第二問(wèn)中,要比較 與
與 的大小,即比較:
的大小,即比較: 與
與 的大小,歸納猜想可得結(jié)論當(dāng)
的大小,歸納猜想可得結(jié)論當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí), ;
;
猜想:當(dāng) 時(shí),
時(shí), 運(yùn)用數(shù)學(xué)歸納法證明即可。
運(yùn)用數(shù)學(xué)歸納法證明即可。
解:⑴取 ,則
,則 ;
…………1分
;
…………1分
對(duì)等式兩邊求導(dǎo),得 ,
,
取 ,則
,則 。 …………4分
。 …………4分
⑵要比較 與
與 的大小,即比較:
的大小,即比較: 與
與 的大小,
的大小,
當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí), ;
…………6分
;
…………6分
猜想:當(dāng) 時(shí),
時(shí), ,下面用數(shù)學(xué)歸納法證明:
,下面用數(shù)學(xué)歸納法證明:
由上述過(guò)程可知, 時(shí)結(jié)論成立,
時(shí)結(jié)論成立,
假設(shè)當(dāng) 時(shí)結(jié)論成立,即
時(shí)結(jié)論成立,即 ,
,
當(dāng) 時(shí),
時(shí),
而
∴
即 時(shí)結(jié)論也成立,
時(shí)結(jié)論也成立,
∴當(dāng) 時(shí),
時(shí), 成立。
…………11分
成立。
…………11分
綜上得,當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí),
(本題滿(mǎn)分18分)第一題滿(mǎn)分4分,第二題滿(mǎn)分6分,第三題滿(mǎn)分8分.
已知橢圓![]() 的長(zhǎng)軸長(zhǎng)是焦距的兩倍,其左、右焦點(diǎn)依次為
的長(zhǎng)軸長(zhǎng)是焦距的兩倍,其左、右焦點(diǎn)依次為![]() 、
、![]() ,拋物線(xiàn)
,拋物線(xiàn)![]()
![]() 的準(zhǔn)線(xiàn)與
的準(zhǔn)線(xiàn)與![]() 軸交于
軸交于![]() ,橢圓
,橢圓![]() 與拋物線(xiàn)
與拋物線(xiàn)![]() 的一個(gè)交點(diǎn)為
的一個(gè)交點(diǎn)為![]() .
.
(1)當(dāng)![]() 時(shí),求橢圓
時(shí),求橢圓![]() 的方程;
的方程;
(2)在(1)的條件下,直線(xiàn)![]() 過(guò)焦點(diǎn)
過(guò)焦點(diǎn)![]() ,與拋物線(xiàn)
,與拋物線(xiàn)![]() 交于
交于![]() 兩點(diǎn),若弦長(zhǎng)
兩點(diǎn),若弦長(zhǎng)![]() 等于
等于![]() 的周長(zhǎng),求直線(xiàn)
的周長(zhǎng),求直線(xiàn)![]() 的方程;
的方程;
(3)由拋物線(xiàn)弧![]()
![]() 和橢圓弧
和橢圓弧![]()
![]()
(![]() )合成的曲線(xiàn)叫“拋橢圓”,是否存在以原點(diǎn)
)合成的曲線(xiàn)叫“拋橢圓”,是否存在以原點(diǎn)![]() 為直角頂點(diǎn),另兩個(gè)頂點(diǎn)
為直角頂點(diǎn),另兩個(gè)頂點(diǎn)![]() 落在“拋橢圓”上的等腰直角三角形
落在“拋橢圓”上的等腰直角三角形![]() ,若存在,求出兩直角邊所在直線(xiàn)的斜率;若不存在,說(shuō)明理由.
,若存在,求出兩直角邊所在直線(xiàn)的斜率;若不存在,說(shuō)明理由.
已知函數(shù)f(x)= ,
, 為常數(shù)。
為常數(shù)。
(I)當(dāng) =1時(shí),求f(x)的單調(diào)區(qū)間;
=1時(shí),求f(x)的單調(diào)區(qū)間;
(II)若函數(shù)f(x)在區(qū)間[1,2]上為單調(diào)函數(shù),求 的取值范圍。
的取值范圍。
【解析】本試題主要考查了導(dǎo)數(shù)在研究函數(shù)中的運(yùn)用。第一問(wèn)中,利用當(dāng)a=1時(shí),f(x)= ,則f(x)的定義域是
,則f(x)的定義域是 然后求導(dǎo),
然后求導(dǎo), ,得到由
,得到由 ,得0<x<1;由
,得0<x<1;由 ,得x>1;得到單調(diào)區(qū)間。第二問(wèn)函數(shù)f(x)在區(qū)間[1,2]上為單調(diào)函數(shù),則
,得x>1;得到單調(diào)區(qū)間。第二問(wèn)函數(shù)f(x)在區(qū)間[1,2]上為單調(diào)函數(shù),則 或
或 在區(qū)間[1,2]上恒成立,即即
在區(qū)間[1,2]上恒成立,即即 ,或
,或 在區(qū)間[1,2]上恒成立,解得a的范圍。
在區(qū)間[1,2]上恒成立,解得a的范圍。
(1)當(dāng)a=1時(shí),f(x)= ,則f(x)的定義域是
,則f(x)的定義域是
 。
。
由 ,得0<x<1;由
,得0<x<1;由 ,得x>1;
,得x>1;
∴f(x)在(0,1)上是增函數(shù),在(1, 上是減函數(shù)。……………6分
上是減函數(shù)。……………6分
(2) 。若函數(shù)f(x)在區(qū)間[1,2]上為單調(diào)函數(shù),
。若函數(shù)f(x)在區(qū)間[1,2]上為單調(diào)函數(shù),
則 或
或 在區(qū)間[1,2]上恒成立。∴
在區(qū)間[1,2]上恒成立。∴ ,或
,或 在區(qū)間[1,2]上恒成立。即
在區(qū)間[1,2]上恒成立。即 ,或
,或 在區(qū)間[1,2]上恒成立。
在區(qū)間[1,2]上恒成立。
又h(x)= 在區(qū)間[1,2]上是增函數(shù)。h(x)max=(2)=
在區(qū)間[1,2]上是增函數(shù)。h(x)max=(2)= ,h(x)min=h(1)=3
,h(x)min=h(1)=3
即
 ,或
,或 。 ∴
。 ∴
 ,或
,或 。
。
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com