題目列表(包括答案和解析)
。
（Ⅰ）求
的極值點；
（Ⅱ）當
時，若方程
在
上有兩個實數解，求實數t的取值范圍；
(Ⅲ）證明：當
時，
。
（10分）設函數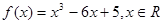
.
⑴ 求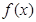
的極值點；
⑵ 若關于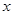
的方程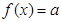
有3個不同實根，求實數a的取值范圍.
⑶ 已知當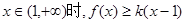
恒成立，求實數k的取值范圍.
。
（Ⅰ）求
的極值點；
（Ⅱ）當
時，若方程
在
上有兩個實數解，求實數t的取值范圍；
(Ⅲ）證明：當
時，
。
（10分）設函數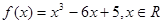
.
⑴ 求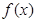
的極值點；
⑵ 若關于
的方程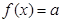
有3個不同實根，求實數a的取值范圍.
⑶ 已知當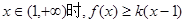
恒成立，求實數k的取值范圍.
。
的極值點；
時，若方程
在
上有兩個實數解，求實數t的取值范圍；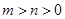
時，
。DCABC CBBAC
11
12 23
13 2
14 4π
15
16解 （1）
1分
2分
由已知有
4分
6分
（2）
10分
= 
11分
= 
12分
17解：（1）設紅球有
個，白球
個，依題意得 1分
，
3分
解得
故紅球有6個．
5分
（2）記“甲取出的球的編號大”為事件A，
所有的基本事件有：(1，2)，(l，3)，(1，4)，
(2，1)，(2，3)，(2，4)，
(3，1)，(3，2)，(3，4)，
(4，1)，(4，2)，(4，3)，
共12個基本事件 8分
事件A包含的基本事件有：(1，2)，(1，3)，（1，4）（2，1），
（2，3），（3，1），（3，2）（4，1），
共8個基本事件
11分
所以，． 
12分
18解：（1）底面三邊長AC=3，BC=4，AB=5，
∠ACB=90°，∴ AC⊥BC， （2分）
又在直三棱柱ABC－A1B1C1中，CC1⊥底面ABC，AC
底面ABC，∴CC1⊥AC，（3分）
BC．CC1平面BCC1，且BC 與CC1相交
∴ AC⊥平面BCC1； （5分）
而BC1平面BCC1
∴ AC⊥BC1 （6分）
（2）設CB1與C1B的交點為E，連結DE，∵ D是AB的中點，E是BC1的中點，
∴ DE//AC1， （8分）
∵ DE平面CDB1，AC1
平面CDB1，
∴ AC1//平面CDB1；（10分）
（3）
（11分）
=
-
（13分）
=20 （14分）
19解：（1）設橢圓的半長軸長．半短軸長．半焦距分別為a,b,c,則有
,
由橢圓定義，有
………1分
＝
……………………………2分
＝
……………………3分
≥
…………………………………………5分
＝
＝
……………………………………………6分
∴的最小值為。
（當且僅當
時，即
取橢圓上下頂點時，取得最小值 ）………………………………………7分
（2）設
的斜率為
，
則
，
…………………………………………8分
…………………………………………9分
∴
＝
及
…………………………………………10分
則＝
＝ 又
…………………………………………12分
∴
…………………………………………13分
故斜率的取值范圍為（
） …………………………………………14分
20解：（1）
，……………………1分
即
，
即
，
，
…………………………………………2分
∴
為等差數列，
…………………………………………3分
又
，
…………………………………………4分
∴
，
…………………………………………5分
∴
…………………………………………7分
（2）
…………………………………………8分
當
時，
…………………………………………11分
，
…………………………………………13分
的整數部分為18。
…………………………………………14分
21解：（1）
………（1分）
由
解得：
………（2分）
當
或
時，
………（3分）
當
時，
………（4分）
所以，有兩個極值點：
是極大值點，
；
………（5分）
是極小值點，
。 ………（6分）
(2) 過點
做直線
，與
的圖象的另一個交點為A
，則
,即
………（8分）
已知有解
，則
解得
………（10分）
當
時，
；
………（11分）
當
時，
，
，
其中當
時，
；………（12分）
當
時，
……（13分）
所以，對任意的
，
的最小值為
（其中當時，）．……（14分）
（以上答案和評分標準僅供參考，其它答案，請參照給分）lf
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com