
題目列表(包括答案和解析)
| 5 |
| 3 |
| 5 |
| 9 |
| 5 |
| 3 |
| 5 |
| 9 |
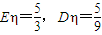 ,求a:b:c.
,求a:b:c.已知函數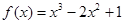 .
.
(1)求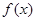 在區間
在區間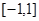 上的最大值;
上的最大值;
(2)若函數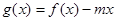 在區間
在區間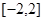 上存在遞減區間,求實數m的取值范圍.
上存在遞減區間,求實數m的取值范圍.
【解析】本試題主要考查了導數在研究函數中的運用,求解函數的最值。第一問中,利用導數求解函數的最值,首先求解導數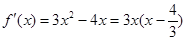 ,然后利用極值和端點值比較大小,得到結論。第二問中,我們利用函數在
,然后利用極值和端點值比較大小,得到結論。第二問中,我們利用函數在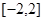 上存在遞減區間,即
上存在遞減區間,即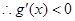 在
在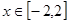 上有解,即
上有解,即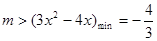 ,即可,可得到。
,即可,可得到。
解:(1)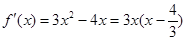 ,
,
令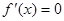 ,解得
,解得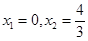 ……………3分
……………3分
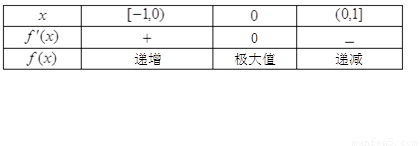
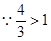 ,
,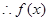 在
在 上為增函數,在
上為增函數,在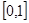 上為減函數,
上為減函數,
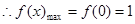 .
…………6分
.
…………6分
(2)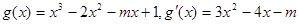
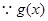 在
在 上存在遞減區間,
上存在遞減區間,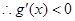 在
在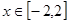 上有解,……9分
上有解,……9分
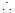
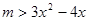 在
在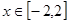 上有解,
上有解,
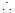
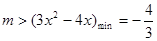 ,
,
所以,實數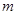 的取值范圍為
的取值范圍為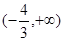
已知函數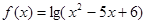 和
和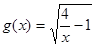 的定義域分別是集合A、B,
的定義域分別是集合A、B,
(1)求集合A,B;
(2)求集合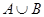 ,
,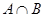 .
.
【解析】本試題考查了集合的基本運算。第一問中,利用
由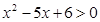 解得
解得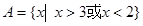
由 解得
解得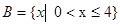
第二問中,由(1)得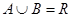
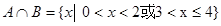
解:(1)由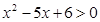 解得
解得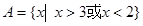 ……………………3分
……………………3分
由 解得
解得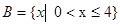 ……………………6分
……………………6分
(2)由(1)得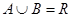 ……………………9分
……………………9分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com