
題目列表(包括答案和解析)
(本小題滿分14分)
已知中心在原點(diǎn)的雙曲線C的一個(gè)焦點(diǎn)是![]() ,一條漸近線的方程是
,一條漸近線的方程是![]() .
.
(Ⅰ)求雙曲線C的方程;
(Ⅱ)若以![]() 為斜率的直線
為斜率的直線![]() 與雙曲線C相交于兩個(gè)不同的點(diǎn)M,N,線段MN的垂直平分線與兩坐標(biāo)軸圍成的三角形的面積為
與雙曲線C相交于兩個(gè)不同的點(diǎn)M,N,線段MN的垂直平分線與兩坐標(biāo)軸圍成的三角形的面積為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
(本小題滿分14分)
已知中心在原點(diǎn),焦點(diǎn)在x軸上的橢圓C的離心率為 ,且經(jīng)過(guò)點(diǎn)(-1,
,且經(jīng)過(guò)點(diǎn)(-1, ),過(guò)點(diǎn)P(2,1)的直線l與橢圓C在第一象限相切于點(diǎn)M.
),過(guò)點(diǎn)P(2,1)的直線l與橢圓C在第一象限相切于點(diǎn)M.
(1)求橢圓C的方程;
(2)求直線l的方程以及點(diǎn)M的坐標(biāo);
(3)是否存在過(guò)點(diǎn)P的直線l 與橢圓C相交于不同的兩點(diǎn)A,B,滿足
與橢圓C相交于不同的兩點(diǎn)A,B,滿足 ·
· =
= ?若存在,求出直線l
?若存在,求出直線l 的方程;若不存在,請(qǐng)說(shuō)明理由.
的方程;若不存在,請(qǐng)說(shuō)明理由.
(本小題滿分14分)已知中心在原點(diǎn),焦點(diǎn)在 軸上,離心率為
軸上,離心率為 的橢圓過(guò)點(diǎn)(
的橢圓過(guò)點(diǎn)( ,
, ).
).
(I)求橢圓方程
(II)設(shè)不過(guò)原點(diǎn)O的直線 :
:
 ,與該橢圓交于P、Q兩點(diǎn),直線OP、OQ的斜率依次為
,與該橢圓交于P、Q兩點(diǎn),直線OP、OQ的斜率依次為 、
、 ,滿足
,滿足 ,求
,求 的值.
的值.
(本小題滿分14分)
已知中心在原點(diǎn)的雙曲線C的一個(gè)焦點(diǎn)是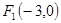 ,一條漸近線的方程是
,一條漸近線的方程是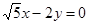 .
.
(Ⅰ)求雙曲線C的方程;
(Ⅱ)若以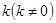 為斜率的直線
為斜率的直線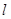 與雙曲線C相交于兩個(gè)不同的點(diǎn)M,N,線段MN的垂直平分線與兩坐標(biāo)軸圍成的三角形的面積為
與雙曲線C相交于兩個(gè)不同的點(diǎn)M,N,線段MN的垂直平分線與兩坐標(biāo)軸圍成的三角形的面積為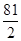 ,求
,求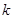 的取值范圍.
的取值范圍.
(本小題滿分14分)已知中心在原點(diǎn)的雙曲線C的右焦點(diǎn)為(2, 0),實(shí)軸長(zhǎng)為![]() .
.
(Ⅰ)求雙曲線C的方程;()
(Ⅱ)若直線l:![]() 與雙曲線C的左支交于A、B兩個(gè)不同點(diǎn),求
與雙曲線C的左支交于A、B兩個(gè)不同點(diǎn),求![]() 的取值范圍;
的取值范圍;
(Ⅲ)在(Ⅱ)的條件下,線段AB的垂直平分線l0與y軸交于M(0,b),求b的取值范圍.
一、選擇題(每題5分共50分)
1.D 2.A 3.B 4.C 5.C
6.C 7.B 8.C 9.C 10.D
二、填空題(每題5分共20分)
11.高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image176.gif) 12.
12.高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image178.gif) 13.
13.高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image180.gif)
14.(0,2),高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image182.gif) 15.3
15.3
三、解答題(共80分)
16.解:(Ⅰ)由已知得:高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image184.gif) ,
,
又高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image186.gif) 是△ABC的內(nèi)角,所以
是△ABC的內(nèi)角,所以高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image188.gif) .
.
(2)由正弦定理:高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image190.gif) ,
,高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image192.gif)
又因?yàn)?sub>高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image194.gif) ,
,高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image196.gif) ,又
,又高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image198.gif) 是△ABC的內(nèi)角,所以
是△ABC的內(nèi)角,所以高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image200.gif) .
.
17.證明:連結(jié)AB,A1D,在正方形中,A1B=A1D,O是BD中點(diǎn),
∴A1O⊥BD;
連結(jié)OM,A高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image202.gif) a=MC1
a=MC1
OA=OC=高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image204.gif) a,AC=
a,AC=高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image206.gif) a,
a,
∴A1O2=A高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image202.gif) a2=
a2=高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image209.gif) a2,OM2=OC2+MC2=
a2,OM2=OC2+MC2=高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image211.gif) a2,A
a2,A高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image213.gif) a2=
a2=高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image215.gif) a2,∴A
a2,∴A
∴A1O⊥OM,
∴AO1⊥平面MBD
18解:(Ⅰ)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image217.gif) ,
,
因?yàn)楹瘮?shù)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image168.gif) 在
在高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image220.gif) 及
及高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image222.gif) 取得極值,則有
取得極值,則有高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image224.gif) ,
,高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image226.gif) .
.
即高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image228.gif)
解得高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image230.gif) ,
,高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image232.gif) .
.
(Ⅱ)由(Ⅰ)可知,高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image234.gif) ,
,
高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image236.gif) .
.
當(dāng)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image238.gif) 時(shí),
時(shí),高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image240.gif) ;
;
當(dāng)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image242.gif) 時(shí),
時(shí),高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image244.gif) ;
;
當(dāng)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image246.gif) 時(shí),
時(shí),高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image240.gif) .
.
所以,當(dāng)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image220.gif) 時(shí),
時(shí),高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image168.gif) 取得極大值
取得極大值高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image251.gif) ,又
,又高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image253.gif) ,
,高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image255.gif) .
.
則當(dāng)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image257.gif) 時(shí),
時(shí),高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image168.gif) 的最大值為
的最大值為高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image255.gif) .
.
因?yàn)閷?duì)于任意的高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image257.gif) ,有
,有高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image262.gif) 恒成立,
恒成立,
所以 高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image264.gif) ,
,
解得 高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image266.gif) 或
或高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image268.gif) ,
,
因此高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image270.gif) 的取值范圍為
的取值范圍為高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image272.gif) .
.
19.解(Ⅰ)由題意知高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image274.gif) ,
,高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image276.gif)
高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image278.gif)
當(dāng)n≥2時(shí),高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image280.gif) ,
,高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image282.gif) ,
,
兩式相減得 高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image284.gif)
整理得:高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image286.gif)
∴數(shù)列{高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image288.gif) }是以2為首項(xiàng),2為公比的等比數(shù)列。
}是以2為首項(xiàng),2為公比的等比數(shù)列。
∴高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image290.gif)
(Ⅱ)由(Ⅰ)知高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image292.gif) ,∴bn=n
,∴bn=n高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image294.gif)
高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image296.gif) , …………①
, …………①
高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image298.gif) , …………②
, …………②
①-②得
高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image300.gif) ,
,
∴高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image302.gif) ,
,
∴高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image304.gif) ,
,
20.解:設(shè)這臺(tái)機(jī)器最佳使用年限是n年,則n年的保養(yǎng)、維修、更換易損零件的總費(fèi)用為:
高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image306.gif)
高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image308.gif) ,
,
高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image310.gif)
高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image312.gif)
等號(hào)當(dāng)且僅當(dāng)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image314.gif)
高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image316.gif)
答:這臺(tái)機(jī)器最佳使用年限是12年,年平均費(fèi)用的最小值為1.55萬(wàn)元.
21.⑴c=2, a=3 雙曲線的方程為
⑵ 得 (1?3k2)x2?6kx?9=0
x1+x2= , x1x2=
由△>0 得 k2<1
由= x1x2+y1y2=(1+k2) x1x2+k(x1+x2)+2>2得 <k2<3
所以,<k2<1
即k∈(?1, )∪( , 1 )
附加題
(1)證明:先將高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image168.gif) 變形:
變形:高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image319.gif) ,
,
當(dāng)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image166.gif) ,即
,即高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image322.gif) 時(shí),∴
時(shí),∴高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image324.gif) 恒成立,
恒成立,
故高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image168.gif) 的定義域?yàn)?sub>
的定義域?yàn)?sub>高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image326.gif) 。
。
反之,若高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image168.gif) 對(duì)所有實(shí)數(shù)
對(duì)所有實(shí)數(shù)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image038.gif) 都有意義,則只須
都有意義,則只須高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image329.gif) 。
。
令高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image331.gif) ,即
,即高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image333.gif) ,解得
,解得高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image322.gif) ,故
,故高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image166.gif) 。
。
(2)解析:設(shè)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image335.gif) ,
,
∵高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image337.gif) 是增函數(shù),
是增函數(shù),
∴當(dāng)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image339.gif) 最小時(shí),
最小時(shí),高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image168.gif) 最小。
最小。
而高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image341.gif) ,
,
顯然,當(dāng)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image343.gif) 時(shí),
時(shí),高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image339.gif) 取最小值為
取最小值為高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image345.gif) ,
,
此時(shí)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image347.gif) 為最小值。
為最小值。
(3)證明:當(dāng)高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image166.gif) 時(shí),
時(shí),高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image349.gif) ,
,
當(dāng)且僅當(dāng)m=2時(shí)等號(hào)成立。
∴高中08-09學(xué)年高二下學(xué)期期中考試(數(shù)學(xué)文).files/image351.gif) 。
。
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com