
題目列表(包括答案和解析)
(本題滿分18分)本題共有3個小題,第1小題滿分3分,第2小題滿分8分,第3小題滿分7分.
已知拋物線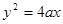 (
(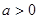 且
且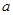 為常數),
為常數), 為其焦點.
為其焦點.
(1)寫出焦點 的坐標;
的坐標;
(2)過點 的直線與拋物線相交于
的直線與拋物線相交于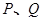 兩點,且
兩點,且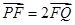 ,求直線
,求直線 的斜率;
的斜率;
(3)若線段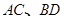 是過拋物線焦點
是過拋物線焦點 的兩條動弦,且滿足
的兩條動弦,且滿足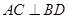 ,如圖所示.求四邊形
,如圖所示.求四邊形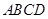 面積的最小值
面積的最小值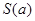 .
.
已知拋物線 (
( 且
且 為常數),
為常數), 為其焦點.
為其焦點.

(1)寫出焦點 的坐標;
的坐標;
(2)過點 的直線與拋物線相交于
的直線與拋物線相交于 兩點,且
兩點,且 ,求直線
,求直線 的斜率;
的斜率;
(3)若線段 是過拋物線焦點
是過拋物線焦點 的兩條動弦,且滿足
的兩條動弦,且滿足 ,如圖所示.求四邊形
,如圖所示.求四邊形 面積的最小值
面積的最小值 .
.
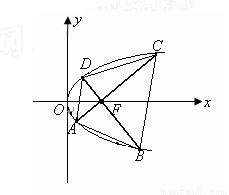
某校同學設計一個如圖所示的“蝴蝶形圖案(陰影區域)”,其中 、
、 是過拋物線
是過拋物線 焦點
焦點 的兩條弦,且其焦點
的兩條弦,且其焦點 ,
, ,點
,點 為
為 軸上一點,記
軸上一點,記 ,其中
,其中 為銳角.
為銳角.

(1)求拋物線 方程;
方程;
(2)求證: .
.
我校某同學設計了一個如圖所示的“蝴蝶形圖案(陰影區域)”來慶祝數學學科節的成功舉辦.其中 、
、 是過拋物線
是過拋物線 焦點
焦點 的兩條弦,且其焦點
的兩條弦,且其焦點 ,
, ,點
,點 為
為 軸上一點,記
軸上一點,記 ,其中
,其中 為銳角.
為銳角.

(1)求拋物線 方程;
方程;
(2)當“蝴蝶形圖案”的面積最小時求 的大小.
的大小.
已知 是過拋物線
是過拋物線 焦點的弦,
焦點的弦, ,則
,則 中點的橫坐標是
中點的橫坐標是
一、選擇題
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
C
C
B
B
A
B
C
D
C
D
二、填空題
13.2 14. 15.60 16.③④
15.60 16.③④
三、解答題
17.解:(1) ,
,
 (2分)
(2分)
又 (4分)
(4分)
 . (6分)
. (6分)
(2)
 (8分)
(8分)

 (10分)
(10分)
18.(1)證明:連結 交
交 于點
于點 ,取
,取 的中點
的中點 ,連結
,連結 ,則
,則 //
// 
 且
且 依題意,知
依題意,知 且
且 ,
,
 ,且
,且 ,
,
故四邊形 是平行四邊形,
是平行四邊形,
 ,即
,即 (4分)
(4分)
又 平面
平面 ,
,

 平面
平面 , (6分)
, (6分)
(2)延長 交
交 的延長線于
的延長線于 點,連結
點,連結 ,作
,作 于
于 點,連結
點,連結 .
.
∵平面 平面
平面 ,平面
,平面 平面
平面 ,
,
 平面
平面 ,
,
∴ 平面
平面 ,
,
由三垂線定理,知 ,故
,故 就是所求二面角的平面角.(8分)
就是所求二面角的平面角.(8分)
∵平面 平面
平面 ,平面
,平面 平面
平面
 平面
平面 ,故
,故 就是直線
就是直線 與平面
與平面 成的角, (10分)
成的角, (10分)
知 設
設 ,則
,則 .
.
在 中:
中:

在 中:由
中:由 ,
, ,知
,知
故平面 與平面
與平面 所成的銳二面角的大小為45°. (12分)
所成的銳二面角的大小為45°. (12分)
19.解:(1)記 表示事無償援助,“取出的2伯產呂中無二等品”,
表示事無償援助,“取出的2伯產呂中無二等品”, 表示事件“取出的2件產品中恰有1件是二等品”。則
表示事件“取出的2件產品中恰有1件是二等品”。則 、
、 互斥,且
互斥,且
故
依題意,知 又
又 ,得
,得 (6分)
(6分)
(2)若該批產品有100件,由(1)知,其中共有二等品100×0.2=20件
記 表示事件“取出的2件產品中無二等品”,則事件
表示事件“取出的2件產品中無二等品”,則事件 與事件
與事件 互斥,
互斥,
依題意,知
故 (12分)
(12分)
20.解:(1) 在
在 上單調遞增,
上單調遞增, 上單調遞減,
上單調遞減,
 有兩根
有兩根 ,2,
,2,
 (6分)
(6分)
(2)令 則
則
因為 在
在 上恒大于0,
上恒大于0,
所以 ,在
,在 上單調遞增,故
上單調遞增,故
 (12分)
(12分)
21.(1)依題意,知
由 ,得
,得
故 ,得
,得 4分
4分
(2)依題意,知
由 ,得
,得
即 ,得
,得 8分
8分
(3)由 、
、 是相互垂直的單位向量,
是相互垂直的單位向量, 知,
知,
得
記數列 的前
的前 項和為
項和為 ,
,
則有

相減得,
故 12分
12分
22.解:(1)設 依題意得
依題意得
 (2分)
(2分)
消去 ,
, ,整理得
,整理得 . (4分)
. (4分)
當 時,方程表示焦點在
時,方程表示焦點在 軸上的橢圓;
軸上的橢圓;
當 時,方程表示焦點在
時,方程表示焦點在 軸上的橢圓;
軸上的橢圓;
當 時,方程表示圓. (6分)
時,方程表示圓. (6分)
(2)當 時,方程為
時,方程為 設直線
設直線 的方程為
的方程為
 (8分)
(8分)
消去 得
得 (10分)
(10分)
根據已知可得 ,故有
,故有
 直線
直線 的斜率為
的斜率為 (12分)
(12分)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com