
題目列表(包括答案和解析)
在極坐標系中,點 到直線
到直線 的距離是
的距離是 
在極坐標系中,點 到直線
到直線 的距離是_______.
的距離是_______.
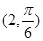 到直線
到直線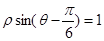 的距離是_______.
的距離是_______.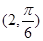 到直線
到直線 的距離是
的距離是 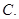
一、選擇題:(每小題5分,共50分)
題號
1
2
3
4
5
6
7
8
9
10
答案
B
D
B
A
C
C
D
A
A
B
二、填空題:(每小題4分,共24分)
11.理科數學.files/image229.gif) ; 12.
; 12.理科數學.files/image231.gif) ; 13.
; 13.理科數學.files/image233.gif) ; 14.
; 14.理科數學.files/image235.gif) ; 15.4 16.120
; 15.4 16.120
三、解答題:(共76分,以下各題為累計得分,其他解法請相應給分)
17.解:(I)理科數學.files/image237.gif)
理科數學.files/image239.gif)
理科數學.files/image241.gif)
由理科數學.files/image243.gif) ,得
,得理科數學.files/image245.gif) 。
。
又當理科數學.files/image247.gif) 時
時理科數學.files/image249.gif) ,得
,得理科數學.files/image251.gif)
理科數學.files/image253.gif)
(Ⅱ)當理科數學.files/image255.gif)
即理科數學.files/image257.gif) 時函數遞增。
時函數遞增。
故理科數學.files/image095.gif) 的單調增區間為
的單調增區間為理科數學.files/image260.gif) ,
,理科數學.files/image262.gif)
又由理科數學.files/image264.gif) ,得
,得理科數學.files/image266.gif) ,
,
由理科數學.files/image268.gif)
解得理科數學.files/image270.gif)
故使理科數學.files/image157.gif) 成立的
成立的理科數學.files/image064.gif) 的集合是
的集合是理科數學.files/image274.gif)
18.解:(I)設袋中有白球理科數學.files/image064.gif) 個,由題意得
個,由題意得理科數學.files/image277.gif) ,
,
即理科數學.files/image279.gif)
解得理科數學.files/image281.gif) 或
或理科數學.files/image283.gif) (舍),故有白球6個
(舍),故有白球6個
(法二,設黑球有理科數學.files/image064.gif) 個,則全是黑球的概率為
個,則全是黑球的概率為理科數學.files/image286.gif) 由
由理科數學.files/image288.gif)
即理科數學.files/image290.gif) ,解得
,解得理科數學.files/image292.gif) 或
或理科數學.files/image294.gif) (舍),故有黑球4個,白球6個
(舍),故有黑球4個,白球6個
(Ⅱ)理科數學.files/image296.gif) ,
,理科數學.files/image298.gif)
理科數學.files/image162.gif)
0
1
2
3
P
理科數學.files/image301.gif)
理科數學.files/image303.gif)
理科數學.files/image305.gif)
理科數學.files/image307.gif)
故分布列為
數學期望理科數學.files/image309.gif)
19.解:(I)取AB的中點O,連接OP,OC
理科數學.files/image311.gif) PA=PB
PA=PB 理科數學.files/image313.gif) PO
PO理科數學.files/image315.gif) AB
AB
又在理科數學.files/image317.gif) 中,
中,理科數學.files/image319.gif) ,
,理科數學.files/image321.gif)
在理科數學.files/image323.gif) 中,
中,理科數學.files/image325.gif) ,又
,又理科數學.files/image172.gif) ,故有
,故有理科數學.files/image328.gif)
理科數學.files/image330.gif) 又
又理科數學.files/image332.gif) ,
,理科數學.files/image334.gif) 面ABC
面ABC
又PO理科數學.files/image336.gif) 面PAB,
面PAB,理科數學.files/image313.gif) 面PAB
面PAB理科數學.files/image315.gif) 面ABC
面ABC
(Ⅱ)以O為坐標原點, 分別以OB,OC,OP為理科數學.files/image064.gif) 軸,
軸,理科數學.files/image341.gif) 軸,
軸,理科數學.files/image119.gif) 軸建立坐標系,
軸建立坐標系,
如圖,則A理科數學.files/image344.gif)
理科數學.files/image346.jpg)
理科數學.files/image348.gif)
理科數學.files/image350.gif)
設平面PAC的一個法向量為理科數學.files/image352.gif) 。
。
理科數學.files/image354.gif) 得
得理科數學.files/image356.gif)
令理科數學.files/image358.gif) ,則
,則理科數學.files/image360.gif)
理科數學.files/image362.gif)
設直線PB與平面PAC所成角為理科數學.files/image364.gif)
于是理科數學.files/image366.gif)
20.解:(I)由題意設C的方程為理科數學.files/image368.gif) 由
由理科數學.files/image370.gif) ,得
,得理科數學.files/image372.gif) 。
。
理科數學.files/image374.gif)
設直線理科數學.files/image180.gif) 的方程為
的方程為理科數學.files/image377.gif) ,由
,由理科數學.files/image379.gif)
②代入①化簡整理得 理科數學.files/image381.gif)
因直線理科數學.files/image180.gif) 與拋物線C相交于不同的兩點,
與拋物線C相交于不同的兩點,
故理科數學.files/image384.gif)
即理科數學.files/image386.gif) ,解得
,解得理科數學.files/image388.gif) 又
又理科數學.files/image390.gif) 時僅交一點,
時僅交一點,理科數學.files/image392.gif)
(Ⅱ)設理科數學.files/image394.gif) ,由由(I)知
,由由(I)知
理科數學.files/image396.gif)
理科數學.files/image398.gif)
理科數學.files/image400.gif)
21.解:(I)當理科數學.files/image196.gif) 時,
時,理科數學.files/image403.gif)
設曲線理科數學.files/image405.gif) 與
與理科數學.files/image407.gif) 在公共點(
在公共點(理科數學.files/image409.gif) )處的切線相同,則有
)處的切線相同,則有理科數學.files/image411.gif)
即理科數學.files/image413.gif) 解得
解得理科數學.files/image415.gif) 或
或理科數學.files/image417.gif) (舍)
(舍)
又理科數學.files/image419.gif) 故得
故得理科數學.files/image421.gif) 公共點為
公共點為理科數學.files/image423.gif) ,
,
理科數學.files/image313.gif) 切線方程為
切線方程為 理科數學.files/image426.gif) ,即
,即理科數學.files/image428.gif)
(Ⅱ)理科數學.files/image430.gif) ,設在(
,設在(理科數學.files/image432.gif) )處切線相同,
)處切線相同,
故有理科數學.files/image434.gif)
即理科數學.files/image436.gif)
由①理科數學.files/image438.gif) ,得
,得理科數學.files/image440.gif) (舍)
(舍)
于是理科數學.files/image442.gif)
令理科數學.files/image444.gif) ,則
,則理科數學.files/image446.gif)
于是當理科數學.files/image448.gif) 即
即理科數學.files/image450.gif) 時,
時,理科數學.files/image452.gif) ,故
,故理科數學.files/image454.gif) 在
在理科數學.files/image456.gif) 上遞增。
上遞增。
當理科數學.files/image458.gif) ,即
,即理科數學.files/image460.gif) 時,
時,理科數學.files/image462.gif) ,故
,故理科數學.files/image454.gif) 在
在理科數學.files/image465.gif) 上遞減
上遞減
理科數學.files/image467.gif) 在
在理科數學.files/image469.gif) 處取最大值。
處取最大值。
理科數學.files/image313.gif) 當
當理科數學.files/image472.gif) 時,b取得最大值
時,b取得最大值理科數學.files/image474.gif)
22.解:(I)理科數學.files/image476.gif) 的對稱軸為
的對稱軸為理科數學.files/image478.gif) ,又當
,又當理科數學.files/image480.gif) 時,
時,理科數學.files/image482.gif) ,
,
故理科數學.files/image484.gif) 在[0,1]上是增函數
在[0,1]上是增函數
理科數學.files/image486.gif) 即
即理科數學.files/image488.gif)
(Ⅱ)理科數學.files/image490.gif)
由理科數學.files/image492.gif)
得理科數學.files/image494.gif)
①―②得理科數學.files/image496.gif) 即
即理科數學.files/image498.gif)
當理科數學.files/image500.gif) 時,
時,理科數學.files/image502.gif) ,當
,當理科數學.files/image504.gif) 時,
時,理科數學.files/image506.gif)
理科數學.files/image508.gif)
于是理科數學.files/image510.gif)
設存在正整數理科數學.files/image183.gif) ,使對
,使對理科數學.files/image480.gif) ,
,理科數學.files/image514.gif) 恒成立。
恒成立。
當理科數學.files/image500.gif) 時,
時,理科數學.files/image517.gif) ,即
,即理科數學.files/image519.gif)
當理科數學.files/image504.gif) 時,
時,理科數學.files/image522.gif)
理科數學.files/image524.gif) 。
。
理科數學.files/image313.gif) 當
當理科數學.files/image527.gif) 時,
時,理科數學.files/image529.gif) ,當
,當理科數學.files/image531.gif) 時,
時,理科數學.files/image533.gif) ,當
,當理科數學.files/image535.gif) 時,
時,理科數學.files/image537.gif)
理科數學.files/image313.gif) 存在正整數
存在正整數理科數學.files/image540.gif) 或8,對于任意正整數
或8,對于任意正整數理科數學.files/image115.gif) 都有
都有理科數學.files/image514.gif) 成立。
成立。
www.ks5u.com
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com