
題目列表(包括答案和解析)
(本題13分)已知函數![]()
(1)已知一直線![]() 經過原點
經過原點![]() 且與曲線
且與曲線![]() 相切,求
相切,求![]() 的直線方程;
的直線方程;
(2)若關于![]() 的方程
的方程![]() 有兩個不等的實根,求實數
有兩個不等的實根,求實數![]() 的取值范圍。
的取值范圍。
已知函數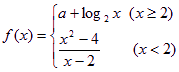 在點
在點![]() 處連續,則常數
處連續,則常數![]() 的值是
的值是
A.2 B.3 C.4 D.5
已知函數![]() 在R上滿足
在R上滿足![]() ,則曲線
,則曲線![]() 在點
在點![]() 處的切線方程是
處的切線方程是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(本題12分)定義在R上的函數![]() ,已知
,已知![]() 在
在![]() 上有最小值3。
上有最小值3。
(1)求![]() 的單調區間;
的單調區間;
(2)求![]() 在
在![]() 上的最大值。
上的最大值。
已知關于![]() 的方程
的方程![]() 有實根
有實根![]() ,復數
,復數![]() ,則復數
,則復數![]() 在復平面內的對應點到原點的距離為
在復平面內的對應點到原點的距離為
A.2 B.4 C.![]() D. 8
D. 8
1.C 2.A 3.B 4.D 5.C 6.B 7.D 8.C 9.B 10.A
11.120° 12.3x+y-1=0 13. 14.10 15.100 16.(1),(4)
14.10 15.100 16.(1),(4)
17.解:(1)設拋物線 ,將(2,2)代入,得p=1. …………4分
,將(2,2)代入,得p=1. …………4分
∴y2=2x為所求的拋物線的方程.………………………………………………………5分
(2)聯立 消去y,得到
消去y,得到 . ………………………………7分
. ………………………………7分
設AB的中點為 ,則
,則 .
.
∴ 點 到準線l的距離
到準線l的距離 .…………………………………9分
.…………………………………9分
而 ,…………………………11分
,…………………………11分
 ,故以AB為直徑的圓與準線l相切.…………………… 12分
,故以AB為直徑的圓與準線l相切.…………………… 12分
(注:本題第(2)也可用拋物線的定義法證明)
18.解:(1)在△ACF中, ,即
,即 .………………………………5分
.………………………………5分
∴ .又
.又 ,∴
,∴ .……………………
7分
.……………………
7分
(2)


 . ……………………………14分
. ……………………………14分
(注:用坐標法證明,同樣給分)
19.
解法一:(1)連OM,作OH⊥SM于H.
∵SM為斜高,∴M為BC的中點,∴BC⊥OM.
∵BC⊥SM,∴BC⊥平面SMO.
又OH⊥SM,∴OH⊥平面SBC.……… 2分
由題意,得 .
.
設SM=x,
則 ,解之
,解之 ,即
,即 .………………… 5分
.………………… 5分
(2)設面EBC∩SD=F,取AD中點N,連SN,設SN∩EF=Q.
 ∵AD∥BC,∴AD∥面BEFC.而面SAD∩面BEFC=EF,∴AD∥EF.
∵AD∥BC,∴AD∥面BEFC.而面SAD∩面BEFC=EF,∴AD∥EF.
又AD⊥SN,AD⊥NM,AD⊥面SMN.
從而EF⊥面SMN,∴EF⊥QS,且EF⊥QM.
∴∠SQM為所求二面角的平面角,記為α.……… 7分
由平幾知識,得 .
.
∴ ,∴
,∴ .
.
∴ ,即所求二面角為
,即所求二面角為 . ……………… 10分
. ……………… 10分
(3)存在一點P,使得OP⊥平面EBC.取SD的中點F,連FC,可得梯形EFCB,
取AD的中點G,連SG,GM,得等腰三角形SGM,O為GM的中點,
設SG∩EF=H,則H是EF的中點.
連HM,則HM為平面EFCB與平面SGM的交線.
又∵BC⊥SO,BC⊥GM,∴平面EFCB⊥平面SGM. …………… 12分
在平面SGM中,過O作OQ⊥HM,由兩平面垂直的性質,可知OQ⊥平面EFCB.
而OQ 平面SOM,在平面SOM中,延長OQ必與SM相交于一點,
平面SOM,在平面SOM中,延長OQ必與SM相交于一點,
故存在一點P,使得OP⊥平面EBC. ……………………… 14分
