
題目列表(包括答案和解析)
(本小題滿分13分)
已知等差數列![]() 滿足
滿足![]() ,若對任意的
,若對任意的![]() ,數列
,數列![]() 滿足
滿足![]() 依次成等比數列,且
依次成等比數列,且![]() =4.
=4.
(Ⅰ)求![]()
(Ⅱ)設![]() ,證明:對任意的
,證明:對任意的![]() ,
,![]()
(本小題滿分13分)
若![]() 為集合
為集合![]() 且
且![]() 的子集,且滿足兩個條件:
的子集,且滿足兩個條件:
①![]() ;
;
②對任意的![]() ,至少存在一個
,至少存在一個![]() ,使
,使![]() 或
或![]() .
.
|
|
| … |
|
|
|
| … |
|
| … | … | … | … |
|
|
| … |
|
則稱集合組![]() 具有性質
具有性質![]() .
.
如圖,作![]() 行
行![]() 列數表,定義數表中的第
列數表,定義數表中的第![]() 行第
行第![]() 列的數為
列的數為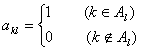 .
.
(Ⅰ)當![]() 時,判斷下列兩個集合組是否具有性質
時,判斷下列兩個集合組是否具有性質![]() ,如果是請畫出所對應的表格,如果不是請說明理由;
,如果是請畫出所對應的表格,如果不是請說明理由;
集合組1:![]() ;
;
集合組2:![]() .
.
(Ⅱ)當![]() 時,若集合組
時,若集合組![]() 具有性質
具有性質![]() ,請先畫出所對應的
,請先畫出所對應的![]() 行3列的一個數表,再依此表格分別寫出集合
行3列的一個數表,再依此表格分別寫出集合![]() ;
;
(Ⅲ)當![]() 時,集合組
時,集合組![]() 是具有性質
是具有性質![]() 且所含集合個數最小的集合組,求
且所含集合個數最小的集合組,求![]() 的值及
的值及![]() 的最小值.(其中
的最小值.(其中![]() 表示集合
表示集合![]() 所含元素的個數)
所含元素的個數)
((本小題滿分13分)
若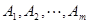 為集合
為集合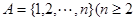 且
且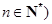 的子集,且滿足兩個條件:
的子集,且滿足兩個條件:
① ;
;
②對任意的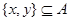 ,至少存在一個
,至少存在一個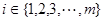 ,使
,使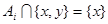 或
或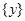 .
.
則稱集合組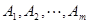 具有性質
具有性質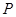 .
.
如圖,作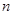 行
行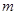 列數表,定義數表中的第
列數表,定義數表中的第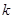 行第
行第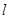 列的數為
列的數為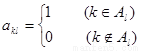 .
.
|
|
|
… |
|
|
|
|
… |
|
|
… |
… |
… |
… |
|
|
|
… |
|
(Ⅰ)當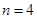 時,判斷下列兩個集合組是否具有性質
時,判斷下列兩個集合組是否具有性質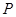 ,如果是請畫出所對應的表格,如果不是請說明理由;
,如果是請畫出所對應的表格,如果不是請說明理由;
集合組1: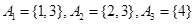 ;
;
集合組2: .
.
(Ⅱ)當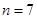 時,若集合組
時,若集合組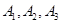 具有性質
具有性質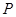 ,請先畫出所對應的
,請先畫出所對應的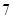 行3列的一個數表,再依此表格分別寫出集合
行3列的一個數表,再依此表格分別寫出集合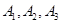 ;
;
(Ⅲ)當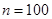 時,集合組
時,集合組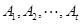 是具有性質
是具有性質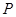 且所含集合個數最小的集合組,求
且所含集合個數最小的集合組,求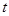 的值及
的值及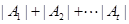 的最小值.(其中
的最小值.(其中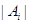 表示集合
表示集合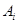 所含元素的個數)
所含元素的個數)
((本小題滿分13分)
若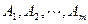 為集合
為集合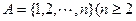 且
且 的子集,且滿足兩個條件:
的子集,且滿足兩個條件:
①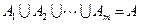 ;
;
②對任意的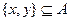 ,至少存在一個
,至少存在一個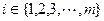 ,使
,使 或
或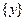 .
.
則稱集合組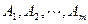 具有性質
具有性質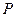 .
.
如圖,作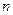 行
行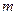 列數表,定義數表中的第
列數表,定義數表中的第 行第
行第 列的數為
列的數為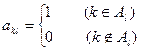 .
.
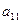 | 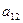 | … |  |
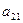 |  | … |  |
| … | … | … | … |
 |  | … |  |
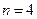 時,判斷下列兩個集合組是否具有性質
時,判斷下列兩個集合組是否具有性質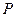 ,如果是請畫出所對應的表格,如果不是請說明理由;
,如果是請畫出所對應的表格,如果不是請說明理由;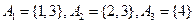 ;
;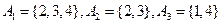 .
.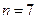 時,若集合組
時,若集合組 具有性質
具有性質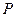 ,請先畫出所對應的
,請先畫出所對應的 行3列的一個數表,再依此表格分別寫出集合
行3列的一個數表,再依此表格分別寫出集合 ;
;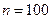 時,集合組
時,集合組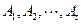 是具有性質
是具有性質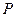 且所含集合個數最小的集合組,求
且所含集合個數最小的集合組,求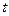 的值及
的值及 的最小值.(其中
的最小值.(其中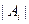 表示集合
表示集合 所含元素的個數)
所含元素的個數)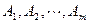 為集合
為集合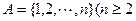 且
且 的子集,且滿足兩個條件:
的子集,且滿足兩個條件: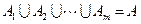 ;
;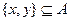 ,至少存在一個
,至少存在一個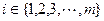 ,使
,使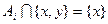 或
或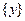 .
.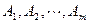 具有性質
具有性質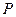 .
.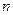 行
行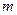 列數表,定義數表中的第
列數表,定義數表中的第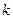 行第
行第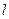 列的數為
列的數為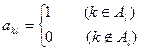 .
.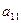 | 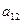 | … | 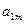 |
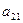 | 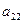 | … | 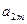 |
| … | … | … | … |
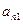 | 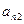 | … | 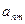 |
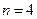 時,判斷下列兩個集合組是否具有性質
時,判斷下列兩個集合組是否具有性質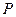 ,如果是請畫出所對應的表格,如果不是請說明理由;
,如果是請畫出所對應的表格,如果不是請說明理由;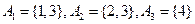 ;
;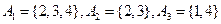 .
.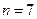 時,若集合組
時,若集合組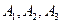 具有性質
具有性質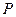 ,請先畫出所對應的
,請先畫出所對應的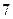 行3列的一個數表,再依此表格分別寫出集合
行3列的一個數表,再依此表格分別寫出集合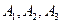 ;
;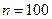 時,集合組
時,集合組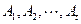 是具有性質
是具有性質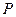 且所含集合個數最小的集合組,求
且所含集合個數最小的集合組,求 的值及
的值及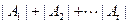 的最小值.(其中
的最小值.(其中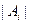 表示集合
表示集合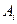 所含元素的個數)
所含元素的個數)湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com