題目列表(包括答案和解析)
”的否定是（ ）
＜0
＜0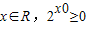
”的否定是（ ）
＜0
＜0命題“存在
，
”的否定是（ ）
A．不存在，
B．存在，
C．對任意的，
D．對任意的，
命題“存在
，
”的否定是（ ）
A．不存在， | B．存在， |
| C．對任意的， | D．對任意的， |
，
”的否定是（ ）A．不存在， | B．存在， |
| C．對任意的， | D．對任意的， |
一．選擇題 (本大題共10小題，每題5分，共50分)
1．C； 2．D； 3，A； 4．B； 5．B；
6．A； 7．B； 8．D； 9．B； 10．D；
二．填空題 (本大題共7小題，每題4分，共28分)
11．
； 12．
，
；
．
； 14．
，
； 15．
； 16．
； 17．
．
三．解答題 (本大題共5小題，第18―20題各14分，第21、22題各15分，共72分)
18．解：(1)因為
，所以
，…………3分
得
，
所以
…………………………………3分
（2）由得
，…………………………………2分
……………………2分
………………………………4分
19．解：（1）
…………………2分
當
時，
…………………2分
∴
，即
∴
是公比為3的等比數列…………………2分
（2）由（1）得：
…………………2分
設
的公差為
（
）， ∵
，∴
………………2分
依題意有
，
，
∴
，得
，或
（舍去）………………2分
故
………………2分
20．解（1）
面
，
由三視圖知：側棱面，
，
∴
∴
面
………………2分
∴
，又
，∴
①………………2分
∵為正方形，∴
，又
∴
②………………2分
由①②知
平面
………………2分
（2）取
的中點
，連結
，
，由題意知
，∴
由三視圖知：側棱
面，∴平面
平面
∴
平面
∴
就是
與面
所成角的平面角………………3分
，。故
，又正方形
中
在
中，∴
，∴
∴
………………3分
綜上知與面所成角的大小的余弦值為
21．解（1）當
，
時，
，………………1分
………………2分
∴當
時
，此時
為減函數，………………1分
當
時
，些時為增函數………………1分
由
，
當時，求函數的最大值
………………2分
（2）
………………1分
①當
時，在
上
，
，
∵在
上為減函數，∴
，則
或
得
………………3分
②當
時，
∵在上為減函數，則
∵
在
上為增函數，在
上為減函數，在
上為增函數，則
得
又，∴………………3分
綜上可知，
的取值范圍為
………………1分
22．（1）記A點到準線距離為，直線
的傾斜角為
，
由拋物線的定義知
，………………………2分
∴
，
∴
………………………3分
（2）設
，
，
由
得
，………………………2分
由
得
且
，同理
……………………2分
由
得
，…………………………2分
即：
，
∴
，…………………………2分
，得
且，
由且得，
的取值范圍為
…………………………2分
命題人
呂峰波(嘉興) 王書朝(嘉善) 王云林(平湖)
胡水林(海鹽) 顧貫石(海寧) 張曉東(桐鄉)
吳明華、張啟源、徐連根、洗順良、李富強、吳林華
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com