
題目列表(包括答案和解析)
設函數 ,若
,若 為函數
為函數 的一個極值點,則下列圖象不可能為
的一個極值點,則下列圖象不可能為 的圖象是
的圖象是

【答案】D
【解析】設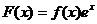 ,∴
,∴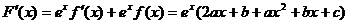 ,
,
又∴ 為
為 的一個極值點,
的一個極值點,
∴ ,即
,即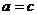 ,
,
∴ ,
,
當 時,
時, ,即對稱軸所在直線方程為
,即對稱軸所在直線方程為 ;
;
當 時,
時, ,即對稱軸所在直線方程應大于1或小于-1.
,即對稱軸所在直線方程應大于1或小于-1.
【答案】![]()
【解析】設![]() ,有幾何意義知
,有幾何意義知![]() 的最小值為
的最小值為![]() , 又因為存在實數x滿足
, 又因為存在實數x滿足![]() ,所以只要2大于等于f(x)的最小值即可.即
,所以只要2大于等于f(x)的最小值即可.即![]() 2,解得:
2,解得:![]() ∈
∈![]() ,所以a的取值范圍是
,所以a的取值范圍是![]() .故答案為:
.故答案為:![]() .
.
設函數 .
.
(I)求 的單調區間;
的單調區間;
(II)當0<a<2時,求函數 在區間
在區間 上的最小值.
上的最小值.
【解析】第一問定義域為真數大于零,得到 .
. .
.
令 ,則
,則 ,所以
,所以 或
或 ,得到結論。
,得到結論。
第二問中, (
( ).
).
 .
.
因為0<a<2,所以 ,
, .令
.令 可得
可得 .
.
對參數討論的得到最值。
所以函數 在
在 上為減函數,在
上為減函數,在 上為增函數.
上為增函數.
(I)定義域為 . ………………………1分
. ………………………1分
 .
.
令 ,則
,則 ,所以
,所以 或
或 . ……………………3分
. ……………………3分
因為定義域為 ,所以
,所以 .
.
令 ,則
,則 ,所以
,所以 .
.
因為定義域為 ,所以
,所以 . ………………………5分
. ………………………5分
所以函數的單調遞增區間為 ,
,
單調遞減區間為 .
………………………7分
.
………………………7分
(II) (
( ).
).
 .
.
因為0<a<2,所以 ,
, .令
.令 可得
可得 .…………9分
.…………9分
所以函數 在
在 上為減函數,在
上為減函數,在 上為增函數.
上為增函數.
①當 ,即
,即 時,
時,
在區間 上,
上, 在
在 上為減函數,在
上為減函數,在 上為增函數.
上為增函數.
所以 . ………………………10分
. ………………………10分
②當 ,即
,即 時,
時, 在區間
在區間 上為減函數.
上為減函數.
所以 .
.
綜上所述,當 時,
時, ;
;
當 時,
時,
如圖,直線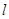 與拋物線
與拋物線 交于
交于 兩點,與
兩點,與 軸相交于點
軸相交于點 ,且
,且 .
.
(1)求證: 點的坐標為
點的坐標為 ;
;
(2)求證: ;
;
(3)求 的面積的最小值.
的面積的最小值.

【解析】設出點M的坐標 ,并把過點M的方程設出來.為避免對斜率不存在的情況進行討論,可以設其方程為
,并把過點M的方程設出來.為避免對斜率不存在的情況進行討論,可以設其方程為 ,然后與拋物線方程聯立消x,根據
,然后與拋物線方程聯立消x,根據 ,即可建立關于
,即可建立關于 的方程.求出
的方程.求出 的值.
的值.
(2)在第(1)問的基礎上,證明: 即可.
即可.
(3)先建立面積S關于m的函數關系式,根據 建立即可,然后再考慮利用函數求最值的方法求最值.
建立即可,然后再考慮利用函數求最值的方法求最值.
如圖,在正方體 中,
中,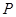 是棱
是棱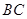 的中點,
的中點,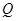 在棱
在棱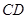 上.
上.
且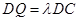 ,若二面角
,若二面角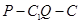 的余弦值為
的余弦值為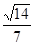 ,求實數
,求實數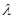 的值.
的值.
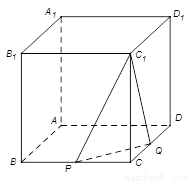
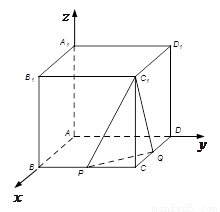
【解析】以A點為坐標原點,AB為x軸,AD為y軸,AA1為z軸,建立空間直角坐標系,設正方體的棱長為4,分別求出平面C1PQ法向量和面C1PQ的一個法向量,然后求出兩法向量的夾角,建立等量關系,即可求出參數λ的值.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com