国产日韩欧美一线二线,美女好全身无遮掩免费网战,亚洲欧美另类卡通乱,日韩av日日夜夜澡,女生抽打女生大骚逼,国产精品99久久…,五月婷婷六月丁香亚洲天堂,中文无码精品一区二区三,日本日p视频免费在线观看

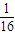
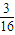
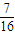
[理]一個袋子里裝有編號為1，2，…，12的12個相同大小的小球，其中1到6號球是紅色球，其余為黑色球．若從中任意摸出一個球，記錄它的顏色和號碼后再放回到袋子里，然后再摸出一個球，記錄它的顏色和號碼，則兩次摸出的球都是紅球，且至少有一個球的號碼是偶數的概率是（ ）
A．
B．
C．
D．

查看答案和解析>>

查看答案和解析>>

一．選擇題（本大題共12小題，每小題5分，共60分．）

D C B B C       D C A C C       A A

二．填空題（本大題共4小題，每小題4分，共16分．）

（13）       （14）        （15）―1        （16）

三．解答題

（17）（本小題滿分12分）

解：（Ⅰ）：

．           3分

依題意，的周期，且，∴ ．∴．

∴ ．                                            5分

∵ [0，], ∴ ≤≤，∴ ≤≤1，

  ∴ 的最小值為 ，即    ∴ ．

∴ ．                                            7分

（Ⅱ）∵ =2， ∴ ．

又 ∵ ∠∈（0，）， ∴ ∠＝．                                  9分

在△ABC中，∵ ，，

∴ ，．解得 ．

又 ∵ 0， ∴ ．                                 12分

（18）（本小題滿分12分）

解：以A點為原點，AB為軸，AD為軸，AD

為軸的空間直角坐標系，如圖所示．則依題意可知相

關各點的坐標分別是A（0，0，0），B（，0，0），

C（，1，0），D（0，1，0），S（0，0，1），

   ∴ M（，1，0），N（，，）．                                  2分

   ∴ （0，，），（，0，0），（，，）．    4分

   ∴ ，．∴ ，．

   ∴ MN ⊥平面ABN．                                                      6分

   （Ⅱ）設平面NBC的法向量為（，，），則，．且又易知 ，．

   ∴   即    ∴

   令，則（，0，）．                                           9分

   顯然，（0，，）就是平面ABN的法向量．

∴ ．

   ∴ 二面角的余弦值是．                                    12分

（19）（本小題滿分12分）

解：（Ⅰ）由題意得

（）；                             3分

同理可得（）；

（）．                           5分

（Ⅱ）．        8分

（Ⅲ）由上問知 ，即是關于的三次函數，設

，則．

令，解得  或 （不合題意，舍去）．

顯然當  時，；當  時，．

∴ 當年產量   時，隨機變量  的期望  取得最大值．              12分

（20）（本小題滿分12分）

解：（Ⅰ）設（，）是函數 的圖象上任意一點，則容易求得點關于直線  的對稱點為（，），依題意點（，）在的圖象上，

∴ ． ∴ ．            2分

∴ ．

∵ 是  的一個極值點，∴ ，解得 ．

∴ 函數  的表達式是 （）．            4分

∴ ．

∵ 函數  的定義域為（）， ∴  只有一個極值點，且顯然當

時，；當時，．

∴ 函數  的單調遞增區間是；單調遞減區間是．           6分

（Ⅱ）由 ，

得 ，∴ ．      9分

∴  在 時恒成立．

∴ 只需求出  在   時的最大值和  在

 時的最小值，即可求得  的取值范圍．

∵ （當  時）；

（當  時）．

∴   的取值范圍是 ．                                         12分

（21）（本小題滿分12分）

解：（Ⅰ）∵ ，

∴．

設O關于直線 的

對稱點為的橫坐標為 ．

又易知直線  解得線段的中點坐標

為（1，－3）．∴．

∴ 橢圓方程為 ．                                           5分

（Ⅱ）顯然直線AN存在斜率，設直線AN的方程為 ，代入 并整理得：． 

設點，，則．

由韋達定理得 ，．                       8分

∵ 直線ME方程為 ，令，得直線ME與x軸的交點的橫坐標 ．

將，代入，并整理得 ．   10分

再將韋達定理的結果代入，并整理可得．

∴ 直線ME與軸相交于定點（，0）．                                  12分

（22）（本小題滿分14分）

證明：（Ⅰ）∵ ，，且 （，N?），

∴  ．                                                            2分

將 去分母，并整理得 ．                      5分

∴ ，，……，，

將這個同向不等式相加，得 ，∴ ．    7分

（Ⅱ）∵ ，∴ ．                     9分

∴ ．即 ．                        11分

∴ ，即

．                                                14分