
題目列表(包括答案和解析)



 的通項公式;
的通項公式; ,若
,若 對
對 恒成立,求實數
恒成立,求實數 的取值范圍;
的取值范圍; 為首項,公比為
為首項,公比為 的數列
的數列 ,
, ,使得數列
,使得數列 中每一項都是數列
中每一項都是數列 中不同的項,若存在,求出所有滿足條件的數列
中不同的項,若存在,求出所有滿足條件的數列 的通項公式;若不存在,說明理由
的通項公式;若不存在,說明理由數列![]() 的通項公式
的通項公式![]()
![]()
(1)求:f(1)、f(2)、f(3)、f(4)的值;
(2)由上述結果推測出計算f(n)的公式,并用數學歸納法加以證明.
設數列![]() 的通項公式為
的通項公式為![]() 。數列
。數列![]() 定義如下:對于正整數m,
定義如下:對于正整數m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若![]() ,求b3; (2)若
,求b3; (2)若![]() ,求數列
,求數列![]() 的前2m項和公式;(3)是否存在p和q,使得
的前2m項和公式;(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范圍;如果不存在,請說明理由。
?如果存在,求p和q的取值范圍;如果不存在,請說明理由。
設數列![]() 的通項公式為
的通項公式為![]() 。數列
。數列![]() 定義如下:對于正整數m,
定義如下:對于正整數m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。
成立的所有n中的最小值。
(1)若![]() ,求b3;
,求b3;
(2)若![]() ,求數列
,求數列![]() 的前2m項和公式;
的前2m項和公式;
(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范圍;如果不存在,請說明理由。
?如果存在,求p和q的取值范圍;如果不存在,請說明理由。
設數列 的通項公式為
的通項公式為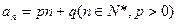 。數列
。數列 定義如下:對于正整數m,
定義如下:對于正整數m, 是使得不等式
是使得不等式 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若 ,求b3; (2)若
,求b3; (2)若 ,求數列
,求數列 的前2m項和公式;(3)是否存在p和q,使得
的前2m項和公式;(3)是否存在p和q,使得 ?如果存在,求p和q的取值范圍;如果不存在,請說明理由。
?如果存在,求p和q的取值范圍;如果不存在,請說明理由。
Ⅰ選擇題
1.C 2. B 3. B 4.B 5.A 6.C 7.A 8.C 9.D 10.A 11.C 12.C
Ⅱ非選擇題
13.  14.
14. 
 15.
15. 16. (2) (3)
16. (2) (3)
17. 解:  (4分)
(4分)
(1)增區間為:  , 減區間為:
, 減區間為: (8分)
(8分)
(2) (12分)
(12分)
18.解:因骰子是均勻的,所以骰子各面朝下的可能性相等,設其中一枚骰子朝下的面上的數字為x,另一枚骰子朝下的面上的數字為y,則 的取值如下表:
的取值如下表:

x+y y
x
1
2
3
5
1
2
3
4
6
2
3
4
5
7
3
4
5
6
8
5
6
7
8
10
從表中可得: (8分)
(8分)
(2)p( =奇數)
=奇數)

 ………………12分
………………12分
19.解:(1)

∴ (2分)
(2分)
又  恒成立 ∴
恒成立 ∴
∴ ∴
∴
∴ (6分)
(6分)
(2)
∴
∴ ①)當  時, 解集為
時, 解集為
②當  時,解集為
時,解集為
③當  時,解集為
時,解集為 (12分)
(12分)
20.解:PD⊥面ABCD ∴DA、DC、DP 相互垂直
建立如圖所示空間直角坐標系Oxyz
(1)


 ∴
∴



∴

 ∴PC⊥DA , PC⊥DE
∴PC⊥DA , PC⊥DE
∴PC⊥面ADE (4分)
(2)∵PD⊥面ABCD PC⊥平面ADE
∴PD與PC夾角為所求
 ∴ 所求二面角E-AD-B的大小為
∴ 所求二面角E-AD-B的大小為 (8分)
(8分)
(3)由(2)得:四邊形ADFE為直角梯形,且 EF=1,DF= ,AD=2
,AD=2
∴ 
∴ 所求部分體積  (12分)
(12分)
21.解:(1)


 為等比數列
為等比數列 






 (4分)
(4分)
(2)



 (6分)
(6分)
(3)






 (7分)
(7分)






 (10分)
(10分)
∴M≥6 
















 (12分)
(12分)
22.解:(1)直線AB的方程為: 與拋物線的切點設為T
與拋物線的切點設為T 且
且
 ∴
∴


∴拋物線c的方程為:  (3分)
(3分)
⑵設直線l的方程為 :
: 易如:
易如:
設 ,
,


①M為AN中點 
由 (Ⅰ)、(Ⅱ)聯解,得  代入(Ⅱ)
代入(Ⅱ)

 4
4
∴直線l的方程為 :  (7分)
(7分)
②
 (9分)
(9分)
FM為∠NFA的平分線
且
 (11分)
(11分)
又

 (14分)
(14分)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com