
題目列表(包括答案和解析)
(12分)如圖,等腰直角△ABC中,![]() ABC
ABC![]() ,EA
,EA![]() 平面ABC,FC//EA,EA = FC = AB =
平面ABC,FC//EA,EA = FC = AB = ![]()
(Ⅰ)求證:AB ![]() 平面BCF;
平面BCF;
(Ⅱ)求二面角A-EB-F的某三角函數值

(12分)如圖,等腰直角△ABC中,![]() ABC
ABC![]() ,EA
,EA![]() 平面ABC,FC//EA,EA = FC = AB =
平面ABC,FC//EA,EA = FC = AB = ![]()
![]() (Ⅰ)求證:AB
(Ⅰ)求證:AB ![]() 平面BCF;
平面BCF;
![]() (Ⅱ)證明五點A.B.C.E.F在同一個球面上,并求A.F兩點的球面距離。
(Ⅱ)證明五點A.B.C.E.F在同一個球面上,并求A.F兩點的球面距離。
![]()
![]()
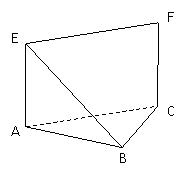
已知:如圖,等腰直角三角形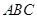 的直角邊
的直角邊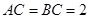 ,沿其中位線
,沿其中位線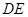 將平面
將平面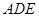 折起,使平面
折起,使平面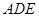 ⊥平面
⊥平面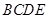 ,得到四棱錐
,得到四棱錐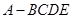 ,設
,設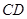 、
、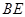 、
、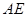 、
、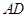 的中點分別為
的中點分別為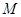 、
、 、
、 、
、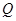 .
.


(1)求證: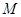 、
、 、
、 、
、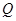 四點共面;
四點共面;
(2)求證:平面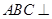 平面
平面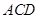 ;
;
(3)求異面直線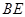 與
與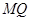 所成的角.
所成的角.
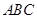 的直角邊
的直角邊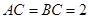 ,沿其中位線
,沿其中位線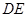 將平面
將平面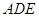 折起,使平面
折起,使平面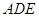 ⊥平面
⊥平面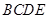 ,得到四棱錐
,得到四棱錐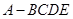 ,設
,設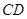 、
、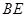 、
、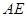 、
、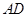 的中點分別為
的中點分別為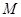 、
、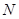 、
、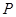 、
、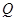 .
.


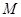 、
、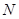 、
、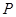 、
、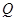 四點共面;
四點共面;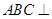 平面
平面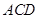 ;
;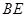 與
與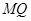 所成的角.
所成的角.已知:如圖,等腰直角三角形 的直角邊
的直角邊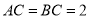 ,沿其中位線
,沿其中位線 將平面
將平面 折起,使平面
折起,使平面 ⊥平面
⊥平面 ,得到四棱錐
,得到四棱錐 ,設
,設 、
、 、
、 、
、 的中點分別為
的中點分別為 、
、 、
、 、
、 .
.



(1)求證: 、
、 、
、 、
、 四點共面;
四點共面;
(2)求證:平面 平面
平面 ;
;
(3)求異面直線 與
與 所成的角.
所成的角.
一、選擇題:
ADBAA BCCDC
二、填空題:
11. 試卷.files/image207.gif) ; 12.
; 12. 試卷.files/image209.gif) ; 13.
; 13.試卷.files/image211.gif)
14(i) ③⑤ (ii) ②⑤ 15.(i)7; (ii)試卷.files/image213.gif) .
.
三、解答題:
16.解:(Ⅰ)試卷.files/image215.gif)
試卷.files/image217.gif)
試卷.files/image219.gif) …………5分
…………5分
由試卷.files/image122.gif) 成等比數列,知
成等比數列,知試卷.files/image221.gif) 不是最大邊
不是最大邊
試卷.files/image223.gif) …………6分
…………6分
(Ⅱ)由余弦定理試卷.files/image225.gif)
試卷.files/image227.gif)
得ac=2 …………11分
試卷.files/image229.gif) =
=試卷.files/image231.gif) …………12分
…………12分
17.解:(Ⅰ)第一天通過檢查的概率為試卷.files/image233.gif) ,
………………………2分
,
………………………2分
第二天通過檢查的概率為試卷.files/image235.gif) ,
…………………………4分
,
…………………………4分
由相互獨立事件得兩天全部通過檢查的概率為試卷.files/image237.gif) . ………………6分
. ………………6分
(Ⅱ)第一天通過而第二天不通過檢查的概率為試卷.files/image239.gif) , …………8分
, …………8分
第二天通過而第一天不通過檢查的概率為試卷.files/image241.gif) ,
………………10分
,
………………10分
由互斥事件得恰有一天通過檢查的概率為試卷.files/image243.gif) . ……………………12分
. ……………………12分
18.解:方法一
試卷.files/image245.gif) (Ⅰ)取
(Ⅰ)取試卷.files/image247.gif) 的中點
的中點試卷.files/image249.gif) ,連結
,連結試卷.files/image251.gif) ,由
,由試卷.files/image253.gif) 知
知試卷.files/image255.gif) ,又
,又試卷.files/image257.gif)
試卷.files/image259.gif) ,故
,故試卷.files/image261.gif) ,所以
,所以試卷.files/image263.gif) 即為二面角
即為二面角試卷.files/image144.gif) 的平面角.
的平面角.
在△試卷.files/image266.gif) 中,
中,試卷.files/image268.gif) ,
,試卷.files/image270.gif) ,
,試卷.files/image272.gif) ,
,
由余弦定理有
試卷.files/image274.gif) ,
,
所以二面角試卷.files/image144.gif) 的大小是
的大小是試卷.files/image276.gif) .
(6分)
.
(6分)
(Ⅱ)由(Ⅰ)知道試卷.files/image278.gif) 平面
平面試卷.files/image266.gif) ,故平面
,故平面試卷.files/image280.gif) 平面
平面試卷.files/image266.gif) ,故
,故試卷.files/image030.gif) 在平面
在平面試卷.files/image283.gif) 上的射影一定在直線
上的射影一定在直線試卷.files/image251.gif) 上,所以點
上,所以點試卷.files/image030.gif) 到平面
到平面試卷.files/image147.gif) 的距離即為△
的距離即為△試卷.files/image266.gif) 的邊
的邊試卷.files/image251.gif) 上的高.
上的高.
故試卷.files/image285.gif) .
…(12分)
.
…(12分)
19.解:(Ⅰ)設試卷.files/image287.gif)
則 試卷.files/image289.gif) ……①
……①
試卷.files/image291.gif) ……②
……②
∴②-①得 2d2=0,∴d=p=0
試卷.files/image293.gif)
試卷.files/image295.gif) ∴
∴試卷.files/image297.gif) …………6分
…………6分
(Ⅱ)當an=n時,恒等式為[S(1,n)]2=S(3,n)
證明:試卷.files/image299.gif)
試卷.files/image301.gif)
相減得: 試卷.files/image303.gif)
∴試卷.files/image305.gif)
試卷.files/image307.gif)
相減得:試卷.files/image309.gif)
又試卷.files/image311.gif)
試卷.files/image313.gif)
又試卷.files/image315.gif)
試卷.files/image316.gif) ∴
∴試卷.files/image318.gif) ………………………………13分
………………………………13分
20.解:(Ⅰ)∵試卷.files/image165.gif) ,∴
,∴試卷.files/image321.gif) ,
,
又∵試卷.files/image167.gif) ,∴
,∴試卷.files/image324.gif) ,
,
∴試卷.files/image326.gif) ,
,
∴橢圓的標準方程為試卷.files/image328.gif) .
………(3分)
.
………(3分)
當試卷.files/image330.gif) 的斜率為0時,顯然
的斜率為0時,顯然試卷.files/image171.gif) =0,滿足題意,
=0,滿足題意,
當試卷.files/image330.gif) 的斜率不為0時,設
的斜率不為0時,設試卷.files/image330.gif) 方程為
方程為試卷.files/image333.gif) ,
,
代入橢圓方程整理得:試卷.files/image335.gif) .
.
試卷.files/image337.gif) ,
,試卷.files/image339.gif) ,
,試卷.files/image341.gif) .
.
則試卷.files/image343.gif)
試卷.files/image345.gif)
試卷.files/image347.gif) ,
,
而試卷.files/image349.gif)
∴試卷.files/image351.gif) ,從而
,從而試卷.files/image171.gif) .
.
綜合可知:對于任意的割線試卷.files/image169.gif) ,恒有
,恒有試卷.files/image171.gif) .
………(8分)
.
………(8分)
(Ⅱ)試卷.files/image356.gif) ,
,
即:試卷.files/image358.gif) ,
,
當且僅當試卷.files/image360.gif) ,即
,即試卷.files/image362.gif) (此時適合于
(此時適合于試卷.files/image364.gif) 的條件)取到等號.
的條件)取到等號.
∴三角形△ABF面積的最大值是試卷.files/image366.gif) . ………………………………(13分)
. ………………………………(13分)
21.解:(Ⅰ)
試卷.files/image368.gif) ……………………………………………4分
……………………………………………4分
(Ⅱ)試卷.files/image370.gif) 或者
或者試卷.files/image372.gif) ……………………………………………8分
……………………………………………8分
(Ⅲ)略 ……………………………………13分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com