
題目列表(包括答案和解析)
已知函數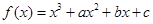 ,曲線
,曲線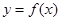 在點
在點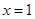 處的切線為
處的切線為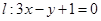 ,若
,若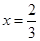 時,
時,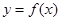 有極值.
有極值.
(1)求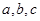 的值;
的值;
(2)求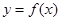 在
在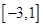 上的最大值和最小值.
上的最大值和最小值.
【解析】(1)根據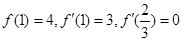 可建立關于a,b,c的三個方程,解方程組即可.
可建立關于a,b,c的三個方程,解方程組即可.
(2)在(1)的基礎上,利用導數列表求極值,最值即可.
已知函數 ,(
,(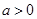 ),
),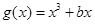
(1)若曲線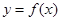 與曲線
與曲線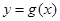 在它們的交點(1,c)處具有公共切線,求a,b的值
在它們的交點(1,c)處具有公共切線,求a,b的值
(2)當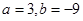 時,若函數
時,若函數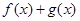 在區間[k,2]上的最大值為28,求k的取值范圍
在區間[k,2]上的最大值為28,求k的取值范圍
【解析】(1)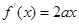 ,
,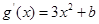
∵曲線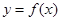 與曲線
與曲線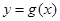 在它們的交點(1,c)處具有公共切線
在它們的交點(1,c)處具有公共切線
∴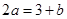 ,
,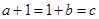
∴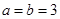
(2)當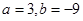 時,
時,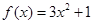 ,
,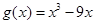 ,
,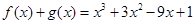
令 ,則
,則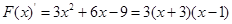 ,令
,令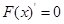 ,
, ∴
∴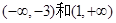 為單調遞增區間,
為單調遞增區間,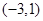 為單調遞減區間,其中F(-3)=28為極大值,所以如果區間[k,2]最大值為28,即區間包含極大值點
為單調遞減區間,其中F(-3)=28為極大值,所以如果區間[k,2]最大值為28,即區間包含極大值點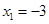 ,所以
,所以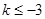
【考點定位】此題應該說是導數題目中較為常規的類型題目,考查的切線,單調性,極值以及最值問題都是課本中要求的重點內容,也是學生掌握比較好的知識點,在題目中能夠發現F(-3)=28,和分析出區間[k,2]包含極大值點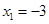 ,比較重要
,比較重要
已知函數 ,
, .
.
(Ⅰ)若函數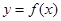 依次在
依次在 處取到極值.求
處取到極值.求 的取值范圍;
的取值范圍;
(Ⅱ)若存在實數 ,使對任意的
,使對任意的 ,不等式
,不等式
 恒成立.求正整數
恒成立.求正整數 的最大值.
的最大值.
【解析】第一問中利用導數在在 處取到極值點可知導數為零可以解得方程有三個不同的實數根來分析求解。
處取到極值點可知導數為零可以解得方程有三個不同的實數根來分析求解。
第二問中,利用存在實數 ,使對任意的
,使對任意的 ,不等式
,不等式
 恒成立轉化為
恒成立轉化為 ,恒成立,分離參數法求解得到范圍。
,恒成立,分離參數法求解得到范圍。
解:(1)
①

(2)不等式  ,即
,即 ,即
,即 .
.
轉化為存在實數 ,使對任意的
,使對任意的 ,不等式
,不等式 恒成立.
恒成立.
即不等式 在
在 上恒成立.
上恒成立.
即不等式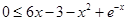 在
在 上恒成立.
上恒成立.
設 ,則.
,則.
設 ,則
,則 ,因為
,因為 ,有
,有 .
.
故 在區間
在區間 上是減函數。又
上是減函數。又
故存在 ,使得
,使得 .
.
當 時,有
時,有 ,當
,當 時,有
時,有 .
.
從而 在區間
在區間 上遞增,在區間
上遞增,在區間 上遞減.
上遞減.
又 [來源:]
[來源:]

所以當 時,恒有
時,恒有 ;當
;當 時,恒有
時,恒有
 ;
;
故使命題成立的正整數m的最大值為5
已知 ,函數
,函數
(1)當 時,求函數
時,求函數 在點(1,
在點(1, )的切線方程;
)的切線方程;
(2)求函數 在[-1,1]的極值;
在[-1,1]的極值;
(3)若在 上至少存在一個實數x0,使
上至少存在一個實數x0,使 >g(xo)成立,求正實數
>g(xo)成立,求正實數 的取值范圍。
的取值范圍。
【解析】本試題中導數在研究函數中的運用。(1)中 ,那么當
,那么當 時,
時, 又
又  所以函數
所以函數 在點(1,
在點(1, )的切線方程為
)的切線方程為 ;(2)中令
;(2)中令 有
有 

對a分類討論 ,和
,和 得到極值。(3)中,設
得到極值。(3)中,設 ,
, ,依題意,只需
,依題意,只需 那么可以解得。
那么可以解得。
解:(Ⅰ)∵ ∴
∴ 
∴ 當 時,
時, 又
又 
∴ 函數 在點(1,
在點(1, )的切線方程為
)的切線方程為 --------4分
--------4分
(Ⅱ)令 有
有 

①
當 即
即 時
時
|
|
(-1,0) |
0 |
(0, |
|
( |
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
極大值 |
|
極小值 |
|
故 的極大值是
的極大值是 ,極小值是
,極小值是
②
當 即
即 時,
時, 在(-1,0)上遞增,在(0,1)上遞減,則
在(-1,0)上遞增,在(0,1)上遞減,則 的極大值為
的極大值為 ,無極小值。
,無極小值。
綜上所述  時,極大值為
時,極大值為 ,無極小值
,無極小值
 時 極大值是
時 極大值是 ,極小值是
,極小值是 ----------8分
----------8分
(Ⅲ)設 ,
,
對 求導,得
求導,得
∵ ,
,

∴  在區間
在區間 上為增函數,則
上為增函數,則
依題意,只需 ,即
,即
解得  或
或 (舍去)
(舍去)
則正實數 的取值范圍是(
的取值范圍是(
 ,
, )
)
已知函數 的圖象過坐標原點O,且在點
的圖象過坐標原點O,且在點 處的切線的斜率是
處的切線的斜率是 .
.
(Ⅰ)求實數 的值;
的值;
(Ⅱ)求 在區間
在區間 上的最大值;
上的最大值;
(Ⅲ)對任意給定的正實數 ,曲線
,曲線 上是否存在兩點P、Q,使得
上是否存在兩點P、Q,使得 是以O為直角頂點的直角三角形,且此三角形斜邊中點在
是以O為直角頂點的直角三角形,且此三角形斜邊中點在 軸上?說明理由.
軸上?說明理由.
【解析】第一問當 時,
時, ,則
,則 。
。
依題意得: ,即
,即 解得
解得
第二問當 時,
時, ,令
,令 得
得 ,結合導數和函數之間的關系得到單調性的判定,得到極值和最值
,結合導數和函數之間的關系得到單調性的判定,得到極值和最值
第三問假設曲線 上存在兩點P、Q滿足題設要求,則點P、Q只能在
上存在兩點P、Q滿足題設要求,則點P、Q只能在 軸兩側。
軸兩側。
不妨設 ,則
,則 ,顯然
,顯然
∵ 是以O為直角頂點的直角三角形,∴
是以O為直角頂點的直角三角形,∴
即 (*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
(*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
若方程(*)無解,不存在滿足題設要求的兩點P、Q.
(Ⅰ)當 時,
時, ,則
,則 。
。
依題意得: ,即
,即 解得
解得
(Ⅱ)由(Ⅰ)知,
①當 時,
時, ,令
,令 得
得
當 變化時,
變化時, 的變化情況如下表:
的變化情況如下表:
|
|
|
0 |
|
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
極小值 |
單調遞增 |
極大值 |
|
又 ,
, ,
, 。∴
。∴ 在
在 上的最大值為2.
上的最大值為2.
②當 時,
時,  .當
.當 時,
時,  ,
, 最大值為0;
最大值為0;
當 時,
時,  在
在 上單調遞增。∴
上單調遞增。∴ 在
在 最大值為
最大值為 。
。
綜上,當 時,即
時,即 時,
時, 在區間
在區間 上的最大值為2;
上的最大值為2;
當 時,即
時,即 時,
時, 在區間
在區間 上的最大值為
上的最大值為 。
。
(Ⅲ)假設曲線 上存在兩點P、Q滿足題設要求,則點P、Q只能在
上存在兩點P、Q滿足題設要求,則點P、Q只能在 軸兩側。
軸兩側。
不妨設 ,則
,則 ,顯然
,顯然
∵ 是以O為直角頂點的直角三角形,∴
是以O為直角頂點的直角三角形,∴
即 (*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
(*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
若方程(*)無解,不存在滿足題設要求的兩點P、Q.
若 ,則
,則 代入(*)式得:
代入(*)式得:
即 ,而此方程無解,因此
,而此方程無解,因此 。此時
。此時 ,
,
代入(*)式得:  即
即 (**)
(**)
令
 ,則
,則
∴ 在
在 上單調遞增, ∵
上單調遞增, ∵  ∴
∴ ,∴
,∴ 的取值范圍是
的取值范圍是 。
。
∴對于 ,方程(**)總有解,即方程(*)總有解。
,方程(**)總有解,即方程(*)總有解。
因此,對任意給定的正實數 ,曲線
,曲線 上存在兩點P、Q,使得
上存在兩點P、Q,使得 是以O為直角頂點的直角三角形,且此三角形斜邊中點在
是以O為直角頂點的直角三角形,且此三角形斜邊中點在 軸上
軸上
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com