
題目列表(包括答案和解析)
(08年昆明市適應考試)(12分)設點![]() ,動圓
,動圓![]() 經(jīng)過點
經(jīng)過點![]() 且和直線
且和直線![]() :
:![]() 相切. 記動圓的圓心
相切. 記動圓的圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)設點![]() 為直線
為直線![]() 上的動點,過點
上的動點,過點![]() 作曲線
作曲線![]() 的切線
的切線![]() (
(![]() 為切點),
為切點),
證明:直線![]() 必過定點并指出定點坐標.
必過定點并指出定點坐標.
(09年萊西一中模擬文)(12分)
設點![]() ,動圓
,動圓![]() 經(jīng)過點
經(jīng)過點![]() 且和直線
且和直線![]() :
:![]() 相切,記動圓的圓心
相切,記動圓的圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)設點![]() 為直線
為直線![]() 上的動點,過點
上的動點,過點![]() 作曲線
作曲線![]() 的切線
的切線![]() (
(![]() 為切點),
為切點),
證明:直線![]() 必過定點并指出定點坐標.
必過定點并指出定點坐標.
[選做題]本題包括A、B、C、D四小題,請選定其中兩題,并在相應的答題區(qū)域內(nèi)作答。若多做,則按作答的前兩題評分。解答時應寫出文字說明、證明過程或演算步驟。
A.  選修4-1:幾何證明選講
選修4-1:幾何證明選講
AB是圓O的直徑,D為圓O上一點,過D作圓O的切線交AB延長線于點C,若DA=DC,求證:AB=2BC。
B. 選修4-2:矩陣與變換
在平面直角坐標系xOy中,已知點A(0,0),B(-2,0),C(-2,1)。設k為非零實數(shù),矩陣M= ,N=
,N= ,點A、B、C在矩陣MN對應的變換下得到點分別為A1、B1、C1,△A1B1C1的面積是△ABC面積的2倍,求k的值。
,點A、B、C在矩陣MN對應的變換下得到點分別為A1、B1、C1,△A1B1C1的面積是△ABC面積的2倍,求k的值。
C. 選修4-4:坐標系與參數(shù)方程
在極坐標系中,已知圓ρ=2cosθ與直線3ρcosθ+4ρsinθ+a=0相切,求實數(shù)a的值。
D. 選修4-5:不等式選講
設a、b是非負實數(shù),求證: 。
。
[必做題]第22題、第23題,每題10分,共計20分。請在答題卡指定區(qū)域內(nèi)作答,解答時應寫出文字說明、證明過程或演算步驟。
選答題(本小題滿分10分)(請考生在第22、23、24三道題中任選一題做答,并用2B鉛筆在答題卡上把所選題目的題號涂黑。注意所做題號必須與所涂題目的題號一致,并在答題卡指定區(qū)域答題。如果多做,則按所做的第一題計分。)
22.選修4-1:幾何證明選講
如圖,已知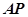 是⊙
是⊙ 的切線,
的切線,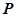 為切點,
為切點,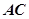 是⊙
是⊙ 的割線,與⊙
的割線,與⊙ 交于
交于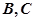 兩點,圓心
兩點,圓心 在
在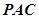 的內(nèi)部,點
的內(nèi)部,點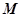 是
是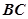 的中點。
的中點。
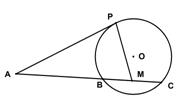
(1)證明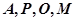 四點共圓;
四點共圓;
(2)求 的大小。
的大小。
23.選修4—4:坐標系與參數(shù)方程[來源:ZXXK]
已知直線 經(jīng)過點
經(jīng)過點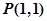 ,傾斜角
,傾斜角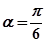 。
。
(1)寫出直線 的參數(shù)方程;
的參數(shù)方程;
(2)設 與曲線
與曲線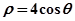 相交于兩點
相交于兩點 ,求點
,求點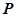 到
到 兩點的距離之積。
兩點的距離之積。
24.選修4—5:不等式證明選講
若不等式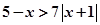 與不等式
與不等式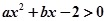 同解,而
同解,而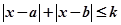 的解集為空集,求實數(shù)
的解集為空集,求實數(shù)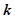 的取值范圍。
的取值范圍。
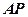 是⊙
是⊙ 的切線,
的切線,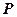 為切點,
為切點,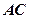 是⊙
是⊙ 的割線,與⊙
的割線,與⊙ 交于
交于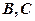 兩點,圓心
兩點,圓心 在
在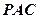 的內(nèi)部,點
的內(nèi)部,點
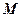 是
是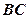 的中點。
的中點。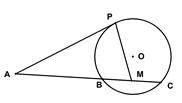
 四點共圓;
四點共圓; 的大小。
的大小。 經(jīng)過點
經(jīng)過點 ,傾斜角
,傾斜角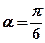 。
。 的參數(shù)方程;
的參數(shù)方程; 與曲線
與曲線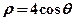 相交于兩點
相交于兩點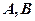 ,求點
,求點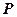 到
到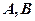 兩點的距離之積。
兩點的距離之積。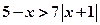 與不等式
與不等式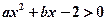 同解,而
同解,而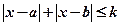 的解集為空集,求實數(shù)
的解集為空集,求實數(shù)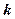 的取值范圍。
的取值范圍。一、選擇題(每小題5分,共60分)
1.A 2.A 3.B 4.D 5.C 6.C 7.B 8.B 9.B 10.D 11.C 12.D
二、填空題(每小題5分,共20分)
13.2 14.學理.files/image317.gif) 15.
15.學理.files/image319.gif) 16.③④
16.③④
三、解答題(共70分)
17. (本小題滿分10分)
解:(Ⅰ)由學理.files/image321.gif) 可得:
可得:學理.files/image323.gif)
學理.files/image325.gif) 又
又學理.files/image327.gif)
學理.files/image329.gif) ; ………………………… 5分
; ………………………… 5分
(Ⅱ)學理.files/image331.gif) ,
,學理.files/image333.gif)
學理.files/image335.gif)
學理.files/image337.gif) .
………………………………………… 10分
.
………………………………………… 10分
18.(本小題滿分12分)
解:(Ⅰ)設A隊得分為2分的事件為學理.files/image339.gif) ,
,
∴學理.files/image341.gif) ………… 4分
………… 4分
(Ⅱ)學理.files/image212.gif) 的可能取值為3 , 2 , 1 , 0 ;
的可能取值為3 , 2 , 1 , 0 ;
學理.files/image344.gif) ,
,
學理.files/image346.gif) ,
, 學理.files/image348.gif) ,
, 學理.files/image350.gif) ,
,
學理.files/image352.gif)
0
1
2
3
學理.files/image354.gif)
學理.files/image356.gif)
學理.files/image358.gif)
學理.files/image360.gif)
∴學理.files/image212.gif) 的分布列為:
的分布列為:
………… 8分
于是 學理.files/image362.gif) , ……………… 9分
, ……………… 9分
∵ 學理.files/image216.gif) , ∴
, ∴ 學理.files/image365.gif) ……………………… 11分
……………………… 11分
由于學理.files/image367.gif) , 故B隊比A隊實力較強. ……………………… 12分
, 故B隊比A隊實力較強. ……………………… 12分
19.(本小題滿分12分)
學理.files/image369.gif) 解法一
解法一
(Ⅰ)連結學理.files/image371.gif) ,
,
∵學理.files/image253.gif) 平面
平面學理.files/image255.gif) ,平面
,平面學理.files/image375.gif) ∩平面
∩平面學理.files/image377.gif)
∴學理.files/image379.gif)
又∵學理.files/image070.gif) 是
是學理.files/image382.gif) 的中點
的中點
∴學理.files/image245.gif) 是
是學理.files/image247.gif) 的中點
的中點
∵學理.files/image386.gif)
∴學理.files/image388.gif) ,
,學理.files/image390.gif)
∴學理.files/image392.gif) 是二面角
是二面角學理.files/image259.gif) 的平面角.
的平面角.
學理.files/image395.gif) ,
,
在直角三角形學理.files/image397.gif) 中,
中,學理.files/image399.gif) ,
,學理.files/image401.gif)
學理.files/image403.gif) ………… 6分
………… 6分
(Ⅱ)解:過學理.files/image405.gif) 作
作學理.files/image407.gif) ,垂足為
,垂足為學理.files/image409.gif) ,連結
,連結學理.files/image411.gif) ,
,學理.files/image413.gif)
∵學理.files/image411.gif) 是三角形
是三角形學理.files/image375.gif) 的中位線,
的中位線,
∴學理.files/image417.gif)
∵學理.files/image419.gif) 面
面學理.files/image421.gif)
∴學理.files/image423.gif) 面
面學理.files/image421.gif)
∴學理.files/image426.gif) ,又
,又學理.files/image428.gif)
∴學理.files/image430.gif) 平面
平面學理.files/image432.gif)
學理.files/image413.gif) 為
為學理.files/image435.gif) 在平面
在平面學理.files/image432.gif) 上的射影,
上的射影,
又∵學理.files/image407.gif) ,由三垂線定理逆定理,得
,由三垂線定理逆定理,得
學理.files/image437.gif)
∴學理.files/image439.gif) 為二面角
為二面角學理.files/image441.gif) 的平面角
的平面角
∵學理.files/image443.gif) ,
,學理.files/image445.gif)
在直角三角形學理.files/image447.gif) 中,
中,學理.files/image449.gif) ,
,學理.files/image451.gif)
學理.files/image453.gif)
∴二面角學理.files/image441.gif) 的大小為
的大小為學理.files/image455.gif) . ……………… 12分
. ……………… 12分
解法二:
(Ⅰ)建立如圖所示空間坐標系學理.files/image457.gif) ,則
,則學理.files/image459.gif) ,
, 學理.files/image461.gif)
學理.files/image463.jpg)
學理.files/image465.gif) ,
,學理.files/image467.gif)
平面學理.files/image469.gif) 的法向量為
的法向量為學理.files/image471.gif) 由
由
學理.files/image473.gif) 得
得學理.files/image475.gif) ,
,
學理.files/image477.gif) 平面
平面學理.files/image479.gif) ,
,學理.files/image481.gif) .
.
所以點學理.files/image245.gif) 是棱
是棱學理.files/image247.gif) 的中點.
的中點.
平面學理.files/image483.gif) 的法向量
的法向量學理.files/image485.gif) ,
,學理.files/image487.gif) ,
,學理.files/image489.gif)
即學理.files/image491.gif)
(Ⅱ)設平面學理.files/image493.gif) 的法向量為
的法向量為學理.files/image495.gif) ,平面
,平面學理.files/image497.gif) 的法向量
的法向量學理.files/image499.gif)
學理.files/image501.gif) ,
,學理.files/image503.gif) ,
,學理.files/image505.gif)
學理.files/image507.gif)
學理.files/image509.gif)
學理.files/image511.gif)
∵二面角學理.files/image513.gif) 為銳角
為銳角
∴二面角學理.files/image513.gif) 的大小為
的大小為學理.files/image515.gif)
20.(本小題滿分12分)
解:(Ⅰ)學理.files/image270.gif) 的定義域為
的定義域為學理.files/image518.gif) .
.
學理.files/image520.gif)
學理.files/image520.gif) ,令
,令學理.files/image523.gif) 得:
得:學理.files/image525.gif)
所以學理.files/image270.gif) 在
在學理.files/image527.gif) 內(nèi)為增函數(shù),在
內(nèi)為增函數(shù),在學理.files/image529.gif) 內(nèi)為減函數(shù). ……………… 6分
內(nèi)為減函數(shù). ……………… 6分
(Ⅱ)由題意得:學理.files/image531.gif) ,
, 學理.files/image533.gif)
學理.files/image535.gif) 為遞增函數(shù),
為遞增函數(shù),學理.files/image537.gif) ;
;
學理.files/image539.gif) 為遞增函數(shù),
為遞增函數(shù), 學理.files/image541.gif)
學理.files/image543.gif) 的取值范圍為
的取值范圍為學理.files/image545.gif) .
……………… 12分
.
……………… 12分
21. (本小題滿分12分)
解:(Ⅰ)過點學理.files/image172.gif) 作
作學理.files/image548.gif) 垂直直線
垂直直線學理.files/image286.gif) 于點
于點學理.files/image551.gif)
依題意得:學理.files/image553.gif) ,
,
所以動點學理.files/image172.gif) 的軌跡為是以
的軌跡為是以學理.files/image279.gif) 為焦點,直線
為焦點,直線學理.files/image286.gif) 為準線的拋物線,
為準線的拋物線,
即曲線學理.files/image288.gif) 的方程是
的方程是學理.files/image558.gif) ………………………4分
………………………4分
(Ⅱ)設學理.files/image560.gif) 、
、學理.files/image562.gif) ,
,學理.files/image564.gif) ,則
,則
由學理.files/image566.gif) 知,
知,學理.files/image568.gif) , ∴
, ∴學理.files/image570.gif) ,
,學理.files/image572.gif)
又∵切線AQ的方程為:學理.files/image574.gif) ,注意到
,注意到學理.files/image576.gif)
切線AQ的方程可化為:學理.files/image578.gif) ;
;
由學理.files/image564.gif) 在切線AQ上, ∴
在切線AQ上, ∴學理.files/image581.gif)
于是學理.files/image560.gif) 在直線
在直線學理.files/image584.gif) 上
上
同理,由切線BQ的方程可得:學理.files/image586.gif)
于是學理.files/image562.gif) 在直線
在直線學理.files/image584.gif) 上
上
所以,直線AB的方程為:學理.files/image584.gif) ,
,
又把學理.files/image590.gif) 代入上式得:
代入上式得:學理.files/image592.gif)
∴直線AB的方程為:學理.files/image594.gif)
∴直線AB必過定點學理.files/image596.gif) .
………………………12分
.
………………………12分
(Ⅱ)解法二:設學理.files/image564.gif) ,切點的坐標為
,切點的坐標為學理.files/image598.gif) ,則
,則
由學理.files/image566.gif) 知,
知,學理.files/image568.gif) ,得切線方程:
,得切線方程:學理.files/image600.gif)
即為:學理.files/image602.gif) ,又∵
,又∵學理.files/image564.gif) 在切線上,
在切線上,
所以可得:學理.files/image604.gif) ,又把
,又把學理.files/image590.gif) 代入上式得:
代入上式得:
學理.files/image606.gif) ,解之得:
,解之得:學理.files/image608.gif)
∴學理.files/image610.gif) ,
,學理.files/image612.gif)
故直線AB的方程為:學理.files/image614.gif)
化簡得:學理.files/image592.gif)
∴直線AB的方程為:學理.files/image594.gif)
∴直線AB必過定點學理.files/image596.gif) .
.
22.(本小題滿分12分)
解:(Ⅰ)由學理.files/image302.gif)
學理.files/image304.gif) ①
①
得:學理.files/image619.gif)
學理.files/image621.gif) ②
②
①-②得學理.files/image623.gif) ,
,
即有學理.files/image625.gif)
學理.files/image621.gif) ,
,
學理.files/image627.gif) 數(shù)列
數(shù)列學理.files/image629.gif) 是從第二項為
是從第二項為學理.files/image631.gif) ,公比為
,公比為學理.files/image633.gif) 的等比數(shù)列
的等比數(shù)列
學理.files/image627.gif)
學理.files/image636.gif) 即
即學理.files/image638.gif)
學理.files/image621.gif) , ……………………5分
, ……………………5分
而學理.files/image300.gif) 滿足該式,
滿足該式, 學理.files/image627.gif)
學理.files/image638.gif)
學理.files/image304.gif) . ……………………6分
. ……………………6分
(Ⅱ)學理.files/image641.gif)
學理.files/image643.gif) ,
, 學理.files/image645.gif) 要使
要使學理.files/image314.gif) 恒成立
恒成立
學理.files/image627.gif)
學理.files/image649.gif) 恒成立
恒成立
即學理.files/image651.gif)
當學理.files/image653.gif) 為奇數(shù)時,
為奇數(shù)時,學理.files/image655.gif) 恒成立,而
恒成立,而學理.files/image657.gif) 的最小值為
的最小值為學理.files/image659.gif)
學理.files/image627.gif)
學理.files/image662.gif) ………………………………………………10分
………………………………………………10分
當學理.files/image653.gif) 為偶數(shù)時,
為偶數(shù)時,學理.files/image665.gif) 恒成立,而
恒成立,而學理.files/image667.gif) 的最大值為
的最大值為學理.files/image669.gif)
學理.files/image627.gif)
學理.files/image672.gif)
學理.files/image627.gif)
學理.files/image675.gif) 或
或學理.files/image677.gif)
所以,存在學理.files/image679.gif) ,使得對任意
,使得對任意學理.files/image312.gif) 都有
都有學理.files/image314.gif) . ……………………………………12分
. ……………………………………12分
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com