国产日韩欧美一线二线,美女好全身无遮掩免费网战,亚洲欧美另类卡通乱,日韩av日日夜夜澡,女生抽打女生大骚逼,国产精品99久久…,五月婷婷六月丁香亚洲天堂,中文无码精品一区二区三,日本日p视频免费在线观看

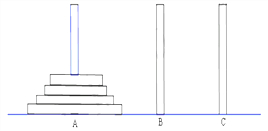古代印度婆羅門(mén)教寺廟內(nèi)的僧侶們?cè)��?jīng)玩過(guò)一種被稱(chēng)為“河內(nèi)寶塔問(wèn)題”的游戲，其玩法如下：如圖，設(shè)有個(gè)圓盤(pán)依其半徑大小，大的在下，小的在上套在柱上，現(xiàn)要將套在柱上的盤(pán)換到柱上，要求每次只能搬動(dòng)一個(gè)，而且任何時(shí)候不允許將大盤(pán)套在小盤(pán)上面，假定有三根柱子可供使用.

現(xiàn)用表示將個(gè)圓盤(pán)全部從柱上移到柱上所至少需要移動(dòng)的次數(shù)，回答下列問(wèn)題：

(1)寫(xiě)出 并求出

(2)記 求和(其中表示所有的積的和)

(3)證明：

古代印度婆羅門(mén)教寺廟內(nèi)的僧侶們?cè)��?jīng)玩過(guò)一種被稱(chēng)為“河內(nèi)寶塔問(wèn)題”的游戲，其玩法如下：如圖，設(shè)有個(gè)圓盤(pán)依其半徑大小，大的在下，小的在上套在柱上，現(xiàn)要將套在柱上的盤(pán)換到柱上，要求每次只能搬動(dòng)一個(gè)，而且任何時(shí)候不允許將大盤(pán)套在小盤(pán)上面，假定有三根柱子可供使用.

現(xiàn)用表示將個(gè)圓盤(pán)全部從柱上移到柱上所至少需要移動(dòng)的次數(shù)，回答下列問(wèn)題：

(1)寫(xiě)出 并求出(2)記 求和

(其中表示所有的積的和)

(3)證明：

如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1.

（Ⅰ）證明PC⊥AD；

（Ⅱ）求二面角A-PC-D的正弦值；

（Ⅲ）設(shè)E為棱PA上的點(diǎn)，滿(mǎn)足異面直線BE與CD所成的角為30°，求AE的長(zhǎng).

【解析】解法一：如圖，以點(diǎn)A為原點(diǎn)建立空間直角坐標(biāo)系，依題意得A(0,0,0)，D(2,0,0),C(0,1,0), 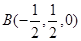,P（0,0,2）.

（1）證明：易得，于是,所以

(2) ,設(shè)平面PCD的法向量，

則,即.不防設(shè)，可得.可取平面PAC的法向量于是從而.

所以二面角A-PC-D的正弦值為.

（3）設(shè)點(diǎn)E的坐標(biāo)為（0,0，h），其中，由此得.

由，故 

所以，，解得，即.

解法二：（1）證明：由，可得，又由,,故.又,所以.

(2)如圖，作于點(diǎn)H，連接DH.由,,可得.

因此,從而為二面角A-PC-D的平面角.在中，,由此得由（1）知,故在中，

因此所以二面角的正弦值為.

（3）如圖，因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012071821180638818491/SYS201207182118431693242163_ST.files/image044.png">，故過(guò)點(diǎn)B作CD的平行線必與線段AD相交，設(shè)交點(diǎn)為F，連接BE，EF. 故或其補(bǔ)角為異面直線BE與CD所成的角.由于BF∥CD，故.在中，故

在中，由,,

可得.由余弦定理，,

所以.