
題目列表(包括答案和解析)
(本題滿分15分) 在△ABC中,已知角A、B、C所對的三條邊分別是a、b、c,且![]()
(1)求證:![]() ;
;
(2)求函數(shù)![]() 的值域。
的值域。
(本題滿分15分) 在△ABC中,已知角A、B、C所對的三條邊分別是a、b、c,且![]()
(1)求證:![]() ;
;
(2)求函數(shù)![]() 的值域。
的值域。
 c,0)三點,其中c>0.
c,0)三點,其中c>0.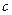 的式子表示);
的式子表示);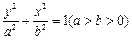 (其中
(其中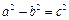 )的左、右頂點分別為D、B,
)的左、右頂點分別為D、B,一、填空題:
1.
一檢測-數(shù)學.files/image192.gif) ,均有x 2+ x +1≥0 2.第一象限 3.充分而不必要條件 4. 0.01
,均有x 2+ x +1≥0 2.第一象限 3.充分而不必要條件 4. 0.01
5. 4 6. 2550 7. 一檢測-數(shù)學.files/image194.gif) 8.①④ 9. R(S1+S2+S3+S4)
8.①④ 9. R(S1+S2+S3+S4)
10.
一檢測-數(shù)學.files/image196.gif) ,11.
,11. 一檢測-數(shù)學.files/image198.gif) 12.1
13.
12.1
13.
一檢測-數(shù)學.files/image200.gif) 14.
14. 一檢測-數(shù)學.files/image202.gif)
二、解答題:
15.(Ⅰ)因為各組的頻率和等于1,故第四組的頻率:
一檢測-數(shù)學.files/image079.gif)
一檢測-數(shù)學.files/image204.gif) 3′
3′
直方圖如右所示 6′
一檢測-數(shù)學.files/image205.gif)
一檢測-數(shù)學.files/image206.gif)
一檢測-數(shù)學.files/image207.gif)
一檢測-數(shù)學.files/image208.gif) (Ⅱ)依題意,60及以上的分數(shù)所在的第三、四、五、六組,頻率和為
(Ⅱ)依題意,60及以上的分數(shù)所在的第三、四、五、六組,頻率和為 一檢測-數(shù)學.files/image210.gif) 所以,抽樣學生成績的合格率是
所以,抽樣學生成績的合格率是一檢測-數(shù)學.files/image212.gif) %.. 9 ′
%.. 9 ′
利用組中值估算抽樣學生的平均分
一檢測-數(shù)學.files/image214.gif)
=一檢測-數(shù)學.files/image216.gif)
一檢測-數(shù)學.files/image190.gif) =71
=71
估計這次考試的平均分是71分 12′
16.(1)證明:連結BD.
在長方體一檢測-數(shù)學.files/image218.gif) 中,對角線
中,對角線一檢測-數(shù)學.files/image220.gif) .
.
又一檢測-數(shù)學.files/image222.gif) E、F為棱AD、AB的中點,
E、F為棱AD、AB的中點,
一檢測-數(shù)學.files/image224.gif) .
.
一檢測-數(shù)學.files/image226.gif) .
.
又B1D1平面一檢測-數(shù)學.files/image228.gif) ,
,一檢測-數(shù)學.files/image230.gif) 平面
平面一檢測-數(shù)學.files/image231.gif) ,
,
一檢測-數(shù)學.files/image233.gif) EF∥平面CB1D1. 6′
EF∥平面CB1D1. 6′
(2)一檢測-數(shù)學.files/image222.gif) 在長方體
在長方體一檢測-數(shù)學.files/image218.gif) 中,AA1⊥平面A1B
中,AA1⊥平面A1B
一檢測-數(shù)學.files/image233.gif) AA1⊥B1D1.
AA1⊥B1D1.
又一檢測-數(shù)學.files/image222.gif) 在正方形A1B
在正方形A1B
一檢測-數(shù)學.files/image233.gif) B1D1⊥平面CAA
B1D1⊥平面CAA
又一檢測-數(shù)學.files/image222.gif) B1D1平面CB1D1,
B1D1平面CB1D1,
一檢測-數(shù)學.files/image233.gif) 平面CAA
平面CAA
17. (1)由一檢測-數(shù)學.files/image096.gif) 得
得一檢測-數(shù)學.files/image238.gif) 4′
4′
由正弦定理得一檢測-數(shù)學.files/image240.gif)
一檢測-數(shù)學.files/image233.gif)
一檢測-數(shù)學.files/image243.gif)
一檢測-數(shù)學.files/image233.gif)
一檢測-數(shù)學.files/image246.gif) 6′
6′
一檢測-數(shù)學.files/image248.gif) 8′
8′
(2)一檢測-數(shù)學.files/image250.gif)
=一檢測-數(shù)學.files/image252.gif) 10′
10′
=一檢測-數(shù)學.files/image254.gif) 12′
12′
由(1)得一檢測-數(shù)學.files/image256.gif)
一檢測-數(shù)學.files/image258.gif)
一檢測-數(shù)學.files/image260.gif)
一檢測-數(shù)學.files/image262.gif) 15′
15′
18.(1)設C:+=1(a>b>0),設c>0,c2=a2-b2,由條件知a-c=,=,
∴a=1,b=c=,
故C的方程為:y2+=1 5′
(2)由=λ,一檢測-數(shù)學.files/image102.gif)
∴λ+1=4,λ=3 或O點與P點重合= 7′
當O點與P點重合=時,m=0
當λ=3時,直線l與y軸相交,則斜率存在。
設l與橢圓C交點為A(x1,y1),B(x2,y2)
得(k2+2)x2+2kmx+(m2-1)=0
Δ=(
x1+x2=, x1x2= 11′
∵=3 ∴-x1=3x2 ∴
消去x2,得3(x1+x2)2+4x1x2=0,∴3()2+4=0
整理得4k
m2=時,上式不成立;m2≠時,k2=,
因λ=3 ∴k≠0 ∴k2=>0,∴-1<m<- 或 <m<1
容易驗證k2>
即所求m的取值范圍為(-1,-)∪(,1)∪{0} 16′
19. ⑴由題意得一檢測-數(shù)學.files/image264.gif) 4′
4′
一檢測-數(shù)學.files/image266.gif)
一檢測-數(shù)學.files/image268.gif) (n≥2),
(n≥2),
又∵一檢測-數(shù)學.files/image157.gif) ,
,一檢測-數(shù)學.files/image271.gif)
一檢測-數(shù)學.files/image266.gif) 數(shù)列
數(shù)列一檢測-數(shù)學.files/image124.gif) 是以
是以一檢測-數(shù)學.files/image274.gif) 為首項,以2為公比的等比數(shù)列。 8′
為首項,以2為公比的等比數(shù)列。 8′
[則一檢測-數(shù)學.files/image276.gif)
一檢測-數(shù)學.files/image266.gif)
一檢測-數(shù)學.files/image278.gif) (
(一檢測-數(shù)學.files/image280.gif) )]
)]
⑵由一檢測-數(shù)學.files/image278.gif) 及
及一檢測-數(shù)學.files/image122.gif) 得
得一檢測-數(shù)學.files/image282.gif)
一檢測-數(shù)學.files/image266.gif)
一檢測-數(shù)學.files/image284.gif) ,
11′
,
11′
則一檢測-數(shù)學.files/image286.gif)
一檢測-數(shù)學.files/image288.gif) 13′
13′
一檢測-數(shù)學.files/image290.gif)
一檢測-數(shù)學.files/image292.gif) 16′
16′
20. (1)設一檢測-數(shù)學.files/image294.gif)
一檢測-數(shù)學.files/image296.gif) ∴
∴一檢測-數(shù)學.files/image298.gif) ∴
∴一檢測-數(shù)學.files/image300.gif)
由一檢測-數(shù)學.files/image302.gif)
又∵一檢測-數(shù)學.files/image304.gif) ∴
∴一檢測-數(shù)學.files/image306.gif)
∴一檢測-數(shù)學.files/image308.gif) 6′
6′
于是一檢測-數(shù)學.files/image310.gif)
由一檢測-數(shù)學.files/image312.gif) 得
得一檢測-數(shù)學.files/image314.gif) 或
或一檢測-數(shù)學.files/image316.gif) ; 由
; 由一檢測-數(shù)學.files/image318.gif) 得
得一檢測-數(shù)學.files/image320.gif) 或
或一檢測-數(shù)學.files/image322.gif)
故函數(shù)一檢測-數(shù)學.files/image130.gif) 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為一檢測-數(shù)學.files/image325.gif) 和
和一檢測-數(shù)學.files/image327.gif) ,
,
單調(diào)減區(qū)間為一檢測-數(shù)學.files/image329.gif) 和
和一檢測-數(shù)學.files/image331.gif) 10′
10′
(2)證明:據(jù)題意一檢測-數(shù)學.files/image146.gif) 且x1<x2<x3,
且x1<x2<x3,
由(1)知f (x1)>f (x2)>f (x3),
一檢測-數(shù)學.files/image333.gif)
一檢測-數(shù)學.files/image335.gif) 14′
14′
一檢測-數(shù)學.files/image337.gif)
一檢測-數(shù)學.files/image339.gif)
即ㄓ一檢測-數(shù)學.files/image152.gif) 是鈍角三角形.
18′
是鈍角三角形.
18′
第Ⅱ部分 加試內(nèi)容
一.必答題:
1.(1)記事件A為“任取兩張卡片,將卡片上的函數(shù)相加得到的函數(shù)是奇函數(shù)”,由題意知一檢測-數(shù)學.files/image341.gif) 4′
4′
(2)ξ可取1,2,3,4.
一檢測-數(shù)學.files/image343.gif) ,
,
一檢測-數(shù)學.files/image345.gif) ; 8′
; 8′
故ξ的分布列為
ξ
1
2
3
4
P
一檢測-數(shù)學.files/image347.gif)
一檢測-數(shù)學.files/image349.gif)
一檢測-數(shù)學.files/image351.gif)
一檢測-數(shù)學.files/image353.gif)
一檢測-數(shù)學.files/image355.gif)
答:ξ的數(shù)學期望為一檢測-數(shù)學.files/image357.gif) 10′
10′
2.(1)由一檢測-數(shù)學.files/image159.gif) 得
得一檢測-數(shù)學.files/image359.gif) ,
,
求得一檢測-數(shù)學.files/image361.gif) 3′
3′
(2)猜想一檢測-數(shù)學.files/image363.gif) 5′
5′
證明:①當n=1時,猜想成立。 6′
②設當n=k時一檢測-數(shù)學.files/image365.gif) 時,猜想成立,即
時,猜想成立,即一檢測-數(shù)學.files/image367.gif) , 7′
, 7′
則當n=k+1時,有一檢測-數(shù)學.files/image369.gif) ,
,
所以當n=k+1時猜想也成立 9′
③綜合①②,猜想對任何一檢測-數(shù)學.files/image371.gif) 都成立。
10′
都成立。
10′
二、選答題:
一檢測-數(shù)學.files/image164.gif) 3.(1)∵DE2=EF?EC,
3.(1)∵DE2=EF?EC,
∴DE : CE=EF: ED.
∵ÐDEF是公共角,
∴ΔDEF∽ΔCED. ∴ÐEDF=ÐC.
∵CD∥AP, ∴ÐC=Ð P.
∴ÐP=ÐEDF.----5′
(2)∵ÐP=ÐEDF, ÐDEF=ÐPEA,
∴ΔDEF∽ΔPEA. ∴DE : PE=EF : EA.即EF?EP=DE?EA.
∵弦AD、BC相交于點E,∴DE?EA=CE?EB.∴CE?EB=EF?EP. 10′
4.(矩陣與變換)
解:.
一檢測-數(shù)學.files/image373.gif) ,
5′
,
5′
橢圓一檢測-數(shù)學.files/image173.gif) 在
在一檢測-數(shù)學.files/image171.gif) 的作用下的新曲線的方程為
的作用下的新曲線的方程為一檢測-數(shù)學.files/image375.gif) 10′
10′
5.(1)直線的參數(shù)方程為一檢測-數(shù)學.files/image377.gif) ,即
,即一檢測-數(shù)學.files/image379.gif) . 5′
. 5′
(2)把直線一檢測-數(shù)學.files/image379.gif) 代入
代入一檢測-數(shù)學.files/image180.gif) ,
,
得一檢測-數(shù)學.files/image381.gif) ,
,一檢測-數(shù)學.files/image383.gif) ,
,
則點一檢測-數(shù)學.files/image184.gif) 到
到一檢測-數(shù)學.files/image182.gif) 兩點的距離之積為
兩點的距離之積為一檢測-數(shù)學.files/image142.gif) .
10′
.
10′
6.
一檢測-數(shù)學.files/image386.gif) 7′
7′
當且僅當一檢測-數(shù)學.files/image388.gif) 且
且一檢測-數(shù)學.files/image390.gif)
F有最小值一檢測-數(shù)學.files/image392.gif) 10′
10′
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com