題目列表(包括答案和解析)
倍后得到點
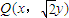，且滿足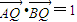
．
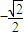的直線l交曲線C于M、N兩點，且
+
+
=
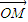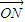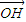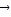，又點H關于原點O的對稱點為點G，試問M、G、N、H四點是否共圓？若共圓，求出圓心坐標和半徑；若不共圓，請說明理由．在平面直角坐標系內已知兩點A(－1，0)、B(1，0)，若將動點P(x，y)的橫坐標保持不變，縱坐標擴大到原來的
倍后得到點Q(x，y)，且滿足
·
＝1．
(Ⅰ)求動點P所在曲線C的方程；
(Ⅱ)過點B作斜率為
的直線l交曲線C于M、N兩點，且
＋
＋
＝
，又點H關于原點O的對稱點為點G，試問M、G、N、H四點是否共圓？若共圓，求出圓心坐標和半徑；若不共圓，請說明理由．
在平面直角坐標系內已知兩點A(－1，0)、B(1，0)，若將動點P(x，y)的橫坐標保持不變，縱坐標擴大到原來的
倍后得到點Q(x，
y)，且滿足
·
＝1．
(Ⅰ)求動點P所在曲線C的方程；
(Ⅱ)過點B作斜率為
的直線l交曲線C于M、N兩點，且
＋
＋
＝
，又點H關于原點O的對稱點為點G，試問M、G、N、H四點是否共圓？若共圓，求出圓心坐標和半徑；若不共圓，請說明理由．
如圖，在平面直角坐標系xOy中．橢圓C：| x2 |
| 2 |
| OT |
| OA |
| x0x |
| 2 |
| OP |
| OM |
| ON |
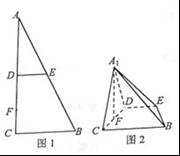
如圖1，在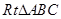
中，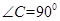
，D,E分別為AC，AB的中點，點F為線段CD上的一點，將
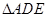沿DE折起到
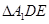的位置，使
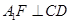，如圖2.
（Ⅰ）求證：DE∥平面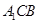
（Ⅱ）求證：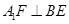
（Ⅲ）線段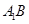
上是否存在點Q，使
？說明理由。
【解析】（1）∵DE∥BC，由線面平行的判定定理得出
（2）可以先證
，得出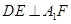
，∵∴
∴
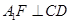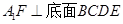
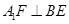
(3)Q為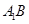的中點，由上問，易知
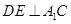,取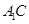
中點P，連接DP和QP，不難證出
，
∴
∴
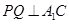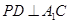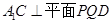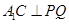,又∵∴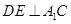
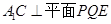
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com