題目列表(包括答案和解析)
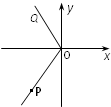如圖，角α 的頂點在直角坐標原點、始邊在y軸的正半軸、終邊經過點P（-3，-4）．角β 的頂點在直角坐標原點、始邊在x 軸的正半軸，終邊OQ落在第二象限，且tanβ=-2．
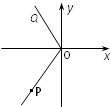如圖，角α 的頂點在直角坐標原點、始邊在y軸的正半軸、終邊經過點P（-3，-4）．角β 的頂點在直角坐標原點、始邊在x 軸的正半軸，終邊OQ落在第二象限，且tanβ=-2．
如圖，角a 的頂點在直角坐標原點、始邊在y軸的正半軸、終邊經過點P（-3，-4）．角b 的頂點在直角坐標原點、始邊在x 軸的正半軸，終邊OQ落在第二象限，且
．
（1）求角a 的正弦值； （2）求∠POQ的余弦值．
說明：
一、本解答指出了每題要考查的主要知識和能力，并給出了一種或幾種解法供參考，如果考生的解答與本解答不同，可根據試題的主要內容比照評分標準制定相應的評分細則．
二、對計算題，當考生的解答 某一步出現錯誤時，如果后繼部分的解答未改變該題的內容和難度，可視影響的程度決定后繼部分的給分，但不得超過該部分正確解答應給分數的一半；如果后繼部分的解答有較嚴重的錯誤，就不再給分．
三、解答右端所注分數，表示考生正確做到這一步應得的累加分數．
四、只給整數分數，選擇題和填空題不給中間分．
一、選擇題：本題主要考查基礎知識和基本運算．
1．B 2．A 3．C 4．B 5．C 6．B
7．C 8．D 9．A 10．D 11．B 12．A
二、本大題:共4個小題；每小題4分，共16分.本題主要考查基礎知識和基本運算．
13．
14．
15．
16．② 、④
三、解答題:本大題共6小題，共74分．解答應寫出文字說明，證明過程或演算步驟．
17．解：．本小題主要考查三角函數的符號，誘導公式，兩角和差公式，二倍角公式，三角函數的圖象及單調性等基本知識以及推理和運算能力．滿分12分．
（1）∵
且sin2
=
∴2sincos= ,sin≥0得cos＞0,從而sin+cos＞0 …3分
∴
=sin+cos=
=
=
…………………………6分
（2）∵
∴
=
……………………………8分
∴時的單調遞增區間為[0，
]和 [
，
].………………………………………12分
18．本小題主要考查直線和平面的位置關系，二面角的大小，點到平面的距離。考查空間想象能力、邏輯推理能力和運算能力．滿分12分．
解法一：（1）在直角梯形ABCD中，過點A作AN垂直BC，
垂足為N，易得BN=1，
，同時四邊形ANCD是矩形，
則CN=1，點N為BC的中點，所以點N與點M重合,
．………2分
連結AM，
因為
平面ABCD，所以
,又AD∥BC，
所以SM
AD．…………………………………4分
（2）過點A作AG垂直SM于點G，
易證平面SAM
,
則
，在RT
中， 
，………………………………………7分
又AD∥平面SBC,所以點D到平面SBC的距離為點A到平面SBC的距離AG,大小值為
；……………8分
（3）取AB中點E，因為
是等邊三角形，所以
,又
,得
，過點E作EF垂直SB于點F，連結CF，則
，所以
是二面角A-SB-C的平面角．………10分
在RT
中，
.在RT
中，
，所以二面角A-SB-C的大小為
．………………………………………………………………………………………12分
解法二：（1）同解法一．
（2）根據（1），如圖所示，分別以AM,AD,AC所在射線為x,y,z軸建立空間直角坐標系．
有A(0,0,0)，M（
，0，0），B（，-1，0），C（,1 ,0），D（0,1 ,0）,S（0,0 ,1）
所以
，
,
．
設平面SBC的法向量
，則
,即
，
解得
，取
．……………………………………………………………………………6分
又
=
，則點D到平面SBC的距離
．………………………………………………………………8分
（3）設平面ASB的法向量
，則
,即
，
解得
，取
．……………………………………………………………………………10分
所以
，則二面角A-SB-C的大小為
．………………………………12分
19．本小題主要考查排列組合與概率的基礎知識，考查推理、運算能力與分類討論思想，以及運用數學知識解決實際問題的能力．滿分12分．
解：（1）
依次成公差大于0的等差數列， 即為甲、乙、丙3個盒中的球數分別為0、1、2，此時的概率
；…………………………………………………………………………3分
(2)解法一:依題意知，
的取值為0、1、2、3．
，…………………………4分
， ………………………………………………6分
，……………………8分
，…………10分
所以，隨機變量的概率分布列為：
0
1
2
3
P
數學期望為
………………………………………………………12分
解法二:把甲、乙兩盒的球數合并成一盒，則每次擲骰子后球放入該盒中的概率
……6分
且
,分布列詳見解法一，…………………………………………………………………… 10分
……………………………………………………………………………………………12分
解法三:令
,則
； 
……………………………………………………6分
，
，分布列詳見解法一，…………………………………………10分
………………………………………………………………………………12分
20．本小題主要考查等比數列和等差數列的概念和性質，以及數列求和的基本運算，考查學生解決數列問題的基本技能，要求學生具備較強的解決數列問題的能力．滿分12分．
解：（1）設等差數列
的公差為
，由
得
，
，………………………………………………………………2分
則
，……………………………………………………………………………3分
， 
，等比數列
的公比
，……………………………………………4分
則
， ………………………………………………………………………………5分
，中的每一項均為中的項；……………………………………………………6分
（2）
，……………………………………………………………7分
由
得：
，………………………………………………………………8分
，
，……………………………………………9分
相減得：
，……………………………………………………………………11分
.……………………………………………………………………12分
21．本小題主要考查橢圓的幾何性質、直線與圓錐曲線的位置關系；考查三角函數、方程、不等式的內容；考查解析幾何思想、分析問題、解決問題的能力．滿分12分．
解法一：（1）設T（x0，y0），由對稱性，不妨設
，∴
，
∴
且
；………………………………………………………………………………1分
∵直線L橢圓E只有一個公共點T，
由橢圓E：
得
，求導得
，……………2分
∴直線L：
，得
；………………………………………………3分
∵直線L在
軸上的截距為
，令
，得
，∴
；
∴直線L斜率的絕對值
；……………………………………………………………5分
（2）直線L：與
的交點
，……………………………………………………………………………6分
設
，在RTDF1AF2和RTDF1BF2中，
，………………………………………………………………………7分
當
時，
∴
……………………………………………………8分
；…………………………………………………………………9分
∵且
，∴
，…………………………10分
∵
最大值為1200，只需令
，
∴
，……………………………………………………………………………………11分
∴
；∴
∴橢圓E的方程為
．…………………………………………………………………………12分
解法二：（1）依題意設直線L：
，代入橢圓E：整理得：
（*），……………………………………………………………………2分
∵直線L橢圓E只有一個公共點T，
∴方程（*）的
，………………………………………………………3分
整理得：
，①
∵直線L在軸上的截距為，∴
代入①得
，∴
；………………………5分
（2）考慮對稱性，不妨設
，由①得
，
直線L：與的交點
，…………………………6分
設，在RTDF1AF2和RTDF1BF2中，
，由①得
，……………………………………………………7分
當時，
∴
…………………………………………………………8分
，…………………………………………………………9分
∵且，∴
，………………………………10分
∵最大值為1200，只需令
，………………………………11分
∴；∴
∴橢圓E的方程為．…………………………………………………………………………12分
22．本小題主要考查函數、數列、不等式、導數等基礎知識，考查應用數學知識分析問題和解決問題的能力，考查數形結合、分類討論、化歸等數學思想方法．滿分12分．
解：（1）令
． ………………………………………1分
令
x
(0,1)
1
(1,+
+
0
－
g(x)
ㄊ
極大值0
ㄋ
根據此表可知，當x=1時，g(x)的最大值為0.
故當x>0時，都有g(x)≤0,即lnx≤x-1. ………………………………………………………3分
(2) 解法一：
……………………………4分
①
當k<0時, 
,∴h(x)在(0,+上是減函數；
又
當x>0且x趨近于零時,h(x)>0.
∴此時h(x)=0在
上有解． …………………………………………………………………5分
②當k>0時, 令
得 x=
(∵x>0)
x
－
0
+
h(x)
ㄋ
極小值
ㄊ
根據此表,當x=,h(x)的最小值為
，………6分
依題意，當≤0，即
時，關于x的方程f(x)=
在上有解，……7分
綜上：k<0或. ……………………………………………………………………………………8分
解法二：當x>0時，lnx=等價于
…………………………………………………4分
令F(x)= 
則
，…………………………………………………………5分
令
得
.
x
+
0
－
F(x)
ㄊ
極小值
ㄋ
根據此表可知, 當x=時,F(x)的最大為
.………………………………………………………………6分
又當x>0且x趨近于零時,F(x)趨向于負無窮大．
依題意，當
，即k<0或,時，關于x的方程f(x)=在上有解，
因此, 實數k的取值范圍為k<0或.………………………………………………………………8分
(3)由(1)可知,當x>1時,
.
令x=k(k
,則
. ……………………………………………………………………9分
于是
=
…………………………………10分
又當m
時,
.
于是
.
故≤
.
所以原不等式成立． …………………………………………………………………………………………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com