
題目列表(包括答案和解析)
已知數列![]() 是正項等比數列,滿足
是正項等比數列,滿足
![]()
(1)求數列![]() 的通項公式;
的通項公式;
(2)記![]() 恒成立,若存在,請求出M的最小值;若不存在,請說明理由。
恒成立,若存在,請求出M的最小值;若不存在,請說明理由。
已知數列![]() 是首項為
是首項為![]() ,公比
,公比![]() 的等比數列. 設
的等比數列. 設![]()
![]() ,數列
,數列![]() 滿足
滿足![]() .
.
(Ⅰ)求證:數列![]() 成等差數列;
成等差數列;
(Ⅱ)求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(Ⅲ)若![]() 對一切正整數
對一切正整數![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
已知數列![]() 是各項均不為0的等差數列,公差為
是各項均不為0的等差數列,公差為![]() ,
,![]() 為其前
為其前![]() 項和,且滿足
項和,且滿足![]() ,
,![]() .數列
.數列![]() 滿足
滿足![]() ,
,![]() 為數列
為數列![]() 的前
的前![]() 項和.
項和.
(1)求![]() ,
,![]() 和
和![]() ;
;
(2)若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)是否存在正整數![]()
![]() ,使得
,使得![]() 成等比數列?若存在,求出所有
成等比數列?若存在,求出所有![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
已知數列 是首項為
是首項為 ,公比
,公比 的等比數列.設
的等比數列.設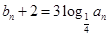 ,
, ,數列
,數列 滿足
滿足 ;
;
(Ⅰ)求證:數列 成等差數列;
成等差數列;
(Ⅱ)求數列 的前
的前 項和
項和 ;
;
(Ⅲ)若 對一切正整數
對一切正整數 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
已知數列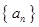 是各項均不為0的等差數列,公差為
是各項均不為0的等差數列,公差為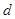 ,
,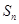 為其前n項和,且滿足
為其前n項和,且滿足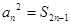 ,
,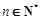 .數列
.數列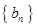 滿足
滿足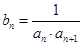 ,
,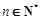 ,
,
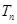 為數列
為數列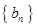 的前
的前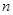 項和.
項和.
(1)求數列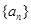 的通項公式
的通項公式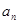 ;
;
(2)若對任意的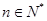 ,不等式
,不等式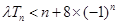 恒成立,求實數
恒成立,求實數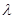 的取值范圍;
的取值范圍;
(3)是否存在正整數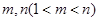 ,使得
,使得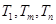 成等比數列?若存在,求出所有
成等比數列?若存在,求出所有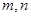
的值;若不存在,請說明理由.
一、選擇題
1-6 C A B B B D 7-12 B C B B B C
二、填空
13. 4 14. .files/image195.gif) 15. 2 16.
15. 2 16..files/image197.gif)
三、解答題
17.(1)解:由.files/image199.gif)
有.files/image201.gif) ……6分
……6分
由.files/image203.gif) , ……8分
, ……8分
由余弦定理.files/image205.gif)
當.files/image207.gif) ……12分
……12分
.files/image208.jpg) ∴PB∥平面EFG. ………………………………3分
∴PB∥平面EFG. ………………………………3分
(2)解:取BC的中點M,連結GM、AM、EM,則GM//BD,