
題目列表(包括答案和解析)
如圖,直線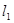 :
: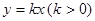 與直線
與直線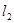 :
: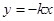 之間的陰影區域(不含邊界)記為
之間的陰影區域(不含邊界)記為 ,其左半部分記為
,其左半部分記為 ,右半部分記為
,右半部分記為 .
.
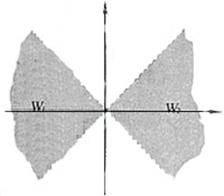
(1)分別用不等式組表示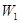 和
和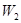 ;
;
(2)若區域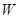 中的動點
中的動點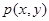 到
到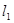 ,
,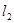 的距離之積等于
的距離之積等于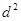 ,求點
,求點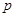 的軌跡
的軌跡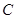 的方程;
的方程;
(05年北京卷)(14分)
如圖,直線![]()
![]() >0)與直線
>0)與直線![]() 之間的陰影區域(不含邊界)記為
之間的陰影區域(不含邊界)記為![]() ,其左半部分記為
,其左半部分記為![]() ,右半部分記為
,右半部分記為![]() .
.
(Ⅰ)分別有不等式組表示![]() 和
和![]() .
.
(Ⅱ)若區域![]() 中的動點
中的動點![]() 到
到![]() 的距離之積等于
的距離之積等于![]() ,求點
,求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅲ)設不過原點![]() 的直線
的直線![]() 與(Ⅱ)中的曲線
與(Ⅱ)中的曲線![]() 相交于
相交于![]() 兩點,且與
兩點,且與![]() 分別交于
分別交于![]() 兩點.求證△
兩點.求證△![]() 的重心與△
的重心與△![]() 的重心重合.
的重心重合.

(本小題滿分14分)
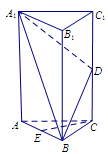
如圖4,在三棱柱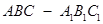 中,△
中,△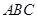 是邊長為
是邊長為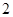 的等邊三角形,
的等邊三角形,
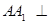 平面
平面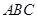 ,
,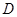 ,
,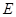 分別是
分別是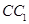 ,
,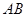 的中點.
的中點.
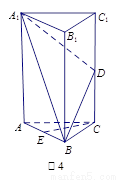
(1)求證: ∥平面
∥平面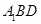 ;
;
(2)若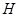 為
為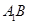 上的動點,當
上的動點,當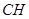 與平面
與平面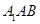 所成最大角的正切值為
所成最大角的正切值為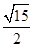 時,
時,
求平面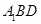 與平面
與平面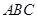 所成二面角(銳角)的余弦值.
所成二面角(銳角)的余弦值.
如圖,在三棱柱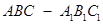 中,△
中,△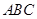 是邊長為
是邊長為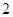 的等邊三角形,
的等邊三角形,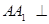 平面
平面 ,
,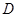 ,
,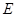 分別是
分別是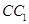 ,
,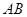 的中點.
的中點.
(1)求證: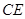 ∥平面
∥平面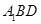 ;
;
(2)若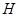 為
為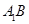 上的動點,當
上的動點,當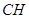 與平面
與平面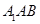 所成最大角的正切值為
所成最大角的正切值為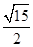 時,求平面
時,求平面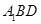 與平面
與平面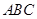 所成二面角(銳角)的余弦值.
所成二面角(銳角)的余弦值.
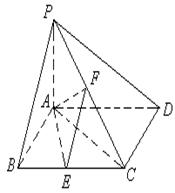
如圖,已知四棱錐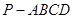 ,底面
,底面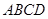 為菱形,
為菱形,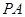
 平面
平面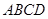 ,
,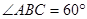 ,
,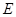 、
、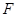 分別是
分別是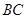 、
、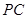 的中點。
的中點。
(1)證明: ;
;
 (2)若
(2)若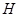 為
為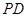 上的動點,
上的動點,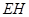 與平面
與平面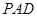 所成最大角的正切值為
所成最大角的正切值為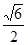 ,求銳二面角
,求銳二面角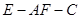 的余弦值;
的余弦值;
(3)在(2)的條件下,設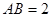 ,求點
,求點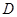 到平面
到平面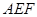 的距離。
的距離。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com