
題目列表(包括答案和解析)
| 1 | 10 |
 如圖是將二進制數11111(2)化為十進制數的一個程序框圖.
如圖是將二進制數11111(2)化為十進制數的一個程序框圖.| 1 | 10 |
.假定平面內的一條直線將該平面內的一個區域分成面積相等的兩個區域,則稱這條直線平分這個區域.如圖, 是平面
是平面 內的任意一個封閉區域.現給出如下結論:
內的任意一個封閉區域.現給出如下結論:
①
過平面 內的任意一點至少存在一條直線平分區域
內的任意一點至少存在一條直線平分區域 ;
;
②過平面 內的任意一點至多存在一條直線平分區域
內的任意一點至多存在一條直線平分區域 ;
;
③
過區域 內的任意一點至少存在兩條直線平分區域
內的任意一點至少存在兩條直線平分區域 ;
;
④
過區域 內的某一點可能存在無數條直線平分區域
內的某一點可能存在無數條直線平分區域 .
.
其中結論正確的是

A.①③ B.①④ C.②③ D.③④
假定平面內的一條直線將該平面內的一個區域分成面積相等的兩個區域,則稱這條直線平分這個區域.如圖, 是平面
是平面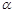 內的任意一個封閉區域.現給出如下結論:
內的任意一個封閉區域.現給出如下結論:

①
過平面內的任意一點至少存在一條直線平分區域 ;
;
②
過平面內的任意一點至多存在一條直線平分區域 ;
;
③
區域 內的任意一點至少存在兩條直線平分區域
內的任意一點至少存在兩條直線平分區域 ;
;
④
平面內存在互相垂直的兩條直線平分區域 成四份.
成四份.
其中正確結論的序號是 .
一、選擇題:本大題共10小題,每小題5分,共50分。在每小題給出的四個選項中,只有 一項是符合題目要求的。
1.B 2.D 3.B 4.C 5.C 6.A 7.A 8.B 9.D 10.C
二、填空題:本大題共5個小題,每小題4分,共20分,把答案填在題中的橫線上。
11.6 12.2 13.80 14. 15.4
15.4
三、解答題:本大題共6小題,共75分。解答應寫文字說明,證明過程或演算步驟.
16.解(1)證明:由 得
得
∴ ………………………………………………4分
………………………………………………4分
(2)由正弦定理得 ∴
∴ ……① …………6分
……① …………6分
又 ,
, =2, ∴
=2, ∴  …………② …………8分
…………② …………8分
解①②得 ,
…………………………………………10分
,
…………………………………………10分
∴ . …………………12分
. …………………12分
17.解:(1)由 得
得 , 即
, 即 又
又 =1 , ∴
=1 , ∴ =3,……2分
=3,……2分
∴ ………………………4分
………………………4分
(2)設
 ,∴
,∴
 ………①
………①
∴
 ………②………………………………7分
………②………………………………7分
①-②得

=
= ……………………………………………10分
……………………………………………10分
∴ , ∴
, ∴ .……………………12分
.……………………12分
18.解:(1)分別取BE、AB的中點M、N,
 連接PM、MC,PN、NC,則PM=1,MB=
連接PM、MC,PN、NC,則PM=1,MB= ,BC=
,BC= ,
,
∴MC= ,而PN=MB=
,而PN=MB= ,
,
NC= ,∴PC=
,∴PC= ,…………………………4分
,…………………………4分
∴
故所求PC與AB所成角的余弦值為 ………6分
………6分
(2)連結AP,∵二面角E-AB-C是直二面角,且AC⊥AB
∴∠BAP即為所求二面角的平面角,即∠BAP=300……8分
在RtΔBAF中,tan∠ABF= ,∴∠ABF=600,
,∴∠ABF=600,
故BF⊥AP, …………………………………………………………10分
又AC⊥面BF,∴BF⊥AC,故BF⊥平面PAC…………………………12分
18.另解:分別以AB、AC、AF為x、y、z軸建立直角坐標系,
則 ,
,
 ∴
∴

而 ,
, ∴
∴
故異面直線PC與AB所成的角的余弦值為 。
。
(2)分別設平面ABC和平面PAC的法向量分別為 ,P點坐標設為
,P點坐標設為 ,則
,則 而
而 ,則由
,則由
 得
得

 且
且 ∴
∴ ,
,
再由 得
得
∴ ,
, ,
,
而
∴ ,即
,即
BF⊥AP,BF⊥AC∴BF⊥平面PAC
19.解:(1)當0<x≤10時, ……2分
……2分
當x >10時, …………4分
…………4分
 …………………………………5分
…………………………………5分
(2)①當0<x≤10時,由
當
∴當x=9時,W取最大值,且 ……9分
……9分
②當x>10時,W=98
當且僅當 …………………………12分
…………………………12分
綜合①、②知x=9時,W取最大值.
所以當年產量為9千件時,該公司在這一品牌服裝生產中獲利最大.……13分
20.解: (1) ………………………2分
………………………2分
即
 ………4分
………4分

∴ 是
是 (也可寫成閉區間)…………6分
(也可寫成閉區間)…………6分
(2) ……………………8分
……………………8分
不等式組所確定的平面區域如圖所示。…………………………………10分


設

 ……………………………………13分
……………………………………13分
 21.(1)
21.(1) B(0,-b)
B(0,-b)
 ,即D為線段FP的中點.,
,即D為線段FP的中點.,
∴ ……………………………2分
……………………………2分
 ,即A、B、D共線.
,即A、B、D共線.
而 

∴ ,得
,得 ,………………………4分
,………………………4分
∴ ………………………………5分
………………………………5分
(2)∵ =2,而
=2,而 ,∴
,∴ ,
,
故雙曲線的方程為 ………①………………………………6分
………①………………………………6分
∴B、的坐標為(0,-1)
設 的方程為
的方程為 …………②
…………②
②代入①得
由題意得: 得:
得: …………9分
…………9分
設M、N的坐標分別為(x1,y1) 、(x2,y2)
則
而

 ………11分
………11分
整理得 , 解得:
, 解得:  或
或 (舍去)
(舍去)
∴所求 的方程為
的方程為 ………………………………13分
………………………………13分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com