
題目列表(包括答案和解析)
已知函數![]() 的反函數為
的反函數為![]() ,若函數
,若函數![]() 的圖象與函數
的圖象與函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱,且
對稱,且![]() ,則實數
,則實數![]() 的值為
的值為
A. ![]() B. 1 C. 2 D. -1
B. 1 C. 2 D. -1
已知函數 的反函數為
的反函數為 ,若函數
,若函數 的圖象與函數
的圖象與函數 的圖象關于直線
的圖象關于直線 對稱,且
對稱,且 ,則實數
,則實數 的值
的值
A. B.1 C.-1 D.2
B.1 C.-1 D.2
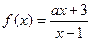 的反函數為
的反函數為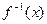 ,若函數
,若函數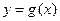 的圖象與函數
的圖象與函數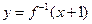 的圖象關于直線
的圖象關于直線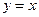 對稱,且
對稱,且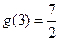 ,則實數
,則實數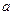 的值為
的值為 A.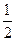 | B.1 | C.2 | D.-1 |
已知函數![]() 的反函數
的反函數![]() ,
,![]() ,若
,若![]() ,則x的取值范圍為
,則x的取值范圍為
A.[0,1]
B.(0,1)
C.(-1,0)
D.[-1,0]
已知函數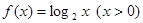 的反函數為
的反函數為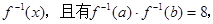 若
若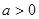 且
且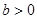 ,則
,則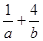 的最小值為 ( )
的最小值為 ( )
A.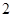 B.
B.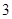 C.
C.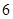 D.
D.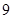
一、選擇題:本大題共10小題,每小題5分,共50分。在每小題給出的四個選項中,只有 一項是符合題目要求的。
1.B 2.D 3.B 4.C 5.C 6.A 7.A 8.B 9.D 10.C
二、填空題:本大題共5個小題,每小題4分,共20分,把答案填在題中的橫線上。
11.6 12.2 13.80 14. 15.4
15.4
三、解答題:本大題共6小題,共75分。解答應寫文字說明,證明過程或演算步驟.
16.解(1)證明:由 得
得
∴ ………………………………………………4分
………………………………………………4分
(2)由正弦定理得 ∴
∴ ……① …………6分
……① …………6分
又 ,
, =2, ∴
=2, ∴  …………② …………8分
…………② …………8分
解①②得 ,
…………………………………………10分
,
…………………………………………10分
∴ . …………………12分
. …………………12分
17.解:(1)由 得
得 , 即
, 即 又
又 =1 , ∴
=1 , ∴ =3,……2分
=3,……2分
∴ ………………………4分
………………………4分
(2)設
 ,∴
,∴
 ………①
………①
∴
 ………②………………………………7分
………②………………………………7分
①-②得

=
= ……………………………………………10分
……………………………………………10分
∴ , ∴
, ∴ .……………………12分
.……………………12分
18.解:(1)分別取BE、AB的中點M、N,
 連接PM、MC,PN、NC,則PM=1,MB=
連接PM、MC,PN、NC,則PM=1,MB= ,BC=
,BC= ,
,
∴MC= ,而PN=MB=
,而PN=MB= ,
,
NC= ,∴PC=
,∴PC= ,…………………………4分
,…………………………4分
∴
故所求PC與AB所成角的余弦值為 ………6分
………6分
(2)連結AP,∵二面角E-AB-C是直二面角,且AC⊥AB
∴∠BAP即為所求二面角的平面角,即∠BAP=300……8分
在RtΔBAF中,tan∠ABF= ,∴∠ABF=600,
,∴∠ABF=600,
故BF⊥AP, …………………………………………………………10分
又AC⊥面BF,∴BF⊥AC,故BF⊥平面PAC…………………………12分
18.另解:分別以AB、AC、AF為x、y、z軸建立直角坐標系,
則 ,
,
 ∴
∴

而 ,
, ∴
∴
故異面直線PC與AB所成的角的余弦值為 。
。
(2)分別設平面ABC和平面PAC的法向量分別為 ,P點坐標設為
,P點坐標設為 ,則
,則 而
而 ,則由
,則由
 得
得

 且
且 ∴
∴ ,
,
再由 得
得
∴ ,
, ,
,
而
∴ ,即
,即
BF⊥AP,BF⊥AC∴BF⊥平面PAC
19.解:(1)當0<x≤10時, ……2分
……2分
當x >10時, …………4分
…………4分
 …………………………………5分
…………………………………5分
(2)①當0<x≤10時,由
當
∴當x=9時,W取最大值,且 ……9分
……9分
②當x>10時,W=98
當且僅當 …………………………12分
…………………………12分
綜合①、②知x=9時,W取最大值.
所以當年產量為9千件時,該公司在這一品牌服裝生產中獲利最大.……13分
20.解: (1) ………………………2分
………………………2分
即
 ………4分
………4分

∴ 是
是 (也可寫成閉區間)…………6分
(也可寫成閉區間)…………6分
(2) ……………………8分
……………………8分
不等式組所確定的平面區域如圖所示。…………………………………10分


設

 ……………………………………13分
……………………………………13分
 21.(1)
21.(1) B(0,-b)
B(0,-b)
 ,即D為線段FP的中點.,
,即D為線段FP的中點.,
∴ ……………………………2分
……………………………2分
 ,即A、B、D共線.
,即A、B、D共線.
而 

∴ ,得
,得 ,………………………4分
,………………………4分
∴ ………………………………5分
………………………………5分
(2)∵ =2,而
=2,而 ,∴
,∴ ,
,
故雙曲線的方程為 ………①………………………………6分
………①………………………………6分
∴B、的坐標為(0,-1)
設 的方程為
的方程為 …………②
…………②
②代入①得
由題意得: 得:
得: …………9分
…………9分
設M、N的坐標分別為(x1,y1) 、(x2,y2)
則
而

 ………11分
………11分
整理得 , 解得:
, 解得:  或
或 (舍去)
(舍去)
∴所求 的方程為
的方程為 ………………………………13分
………………………………13分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com