題目列表(包括答案和解析)
| AB |
| AB |
| AP |
| π |
| 4 |
| AB |
| AB |
| AP |
| 2 |
| 2 |
| π |
| 4 |
已知對任意平面向量
=(x,y),把繞其起點沿逆時針方向旋轉
角得到向量
，叫做把點B繞點A逆時針方向旋轉角得到點P. 設平面內曲線C上的每一點繞原點沿逆時針方向旋轉
后得到點的軌跡是曲線
，則原來曲線C的方程是____▲_____
| AB |
| AB |
| AP |
| π |
| 4 |
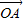=（0，1）、
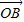=（0，3），把向量
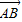繞點A逆時針旋轉90°得到向量
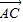，則向量
等于（ ）一、選擇題
ADBBD ABBAD
二、填空題
11、
12、
13、C
14、21 15、
16、（-，0）
三、解答題
17、解：（1）
4分
∵f（x）的最小值為3
所以-a+
=3,a=2
∴f(x)=-2sin(2x+
)+5
6分
（2）因為(-
)變為了(
)，所以h=
,k=-5
由圖象變換得
=-2sin(2x-
)
8分
由2kp+
≤2x-≤2kp+
得kp+
≤x≤kp+
所以單調增區間為
[kp+, kp+](k∈Z) 13分
18、解：（1）如圖，在四棱錐
中，
∵BC∥AD，從而點D到平面PBC間的距離等于點A
到平面PBC的距離. 2分
∵∠ABC=
，∴AB⊥BC，
又PA⊥底面ABCD，∴PA⊥BC，
∴BC⊥平面 PAB， 4分
∴平面PAB⊥平面PBC，交線為PB，
過A作AE⊥PB，垂足為E，則AE⊥平面PBC，
∴AE的長等于點D到平面PBC的距離．
而
，∴
．
即點D到平面PBC的距離為
．
6分
（2）依題意依題意四棱錐P-ABCD的體積為
，
∴（BC+AD）AB×PA=
，∴
，
8分
平面PDC在平面PAB上的射影為PAB，SPAB=
，
10分
PC=
，PD=
，DC=
，SPDC=
a2,
12分
設平面PDC和平面PAB所成二面角為q，則cosq=
=
q=arccos. 13分
19、解：（1）從10 道不同的題目中不放回地隨機抽取3次，每次只抽取1道題，抽法總數為
只有第一次抽到藝術類數目的抽法總數為
∴
5分
（2）抽到體育類題目的可能取值為0，1，2，3則
∴
的分布列為
0
1
2
3
P
10分
11分
從而有
13分
20、解:（1）設
與
在公共點
處的切線相同
1分
由題意知
，∴
3分
由
得，
，或
（舍去）
即有
5分
（2）設與在公共點處的切線相同
由題意知 ，∴
由
得，
，或
（舍去）
7分
即有
8分
令
，則
，于是
當
，即
時，
；
當
，即
時，
11分
故
在
的最大值為
，故
的最大值為
13分
21、解:(1)∵且｜PF1｜＋｜PF2｜＝
∴P的軌跡為以F1、F2為焦點的橢圓E，可設E：(其中b2＝a2－5) 2分
在△PF
又
∴當且僅當| PF1 |＝| PF2 |時，| PF1 |?| PF2 |取最大值， 4分
此時cos∠F1PF2取最小值
令＝
a2＝9，
∵c＝ ∴b2＝4故所求P的軌跡方程為 6分
(2)設N(s，t)，M(x，y)，則由，可得(x，y－3)＝λ(s，t－3)
∴x＝λs，y＝3＋λ(t－3) 7分
而M、N在動點P的軌跡上，故且
消去S得解得 10分
又| t |≤2，∴，解得，故λ的取值范圍是[，5] 12分
22、解：（1）由
，得
，代入
，得
，
整理，得
,從而有
，
，
是首項為1，公差為1的等差數列，
即
. 4分
（2）
， 
，
，
，
. 8分
(3)∵
.
由（2）知
，
，
.
12分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com