
題目列表(包括答案和解析)
設函數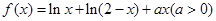 .
.
(Ⅰ) 當 時,求
時,求 的單調區間;
的單調區間;
(Ⅱ) 若 在
在 上的最大值為
上的最大值為 ,求
,求 的值.
的值.
【解析】第一問中利用函數 的定義域為(0,2),
的定義域為(0,2), .
.
當a=1時, 所以
所以 的單調遞增區間為(0,
的單調遞增區間為(0, ),單調遞減區間為(
),單調遞減區間為( ,2);
,2);
第二問中,利用當 時,
時, >0, 即
>0, 即 在
在 上單調遞增,故
上單調遞增,故 在
在 上的最大值為f(1)=a 因此a=1/2.
上的最大值為f(1)=a 因此a=1/2.
解:函數 的定義域為(0,2),
的定義域為(0,2), .
.
(1)當 時,
時, 所以
所以 的單調遞增區間為(0,
的單調遞增區間為(0, ),單調遞減區間為(
),單調遞減區間為( ,2);
,2);
(2)當 時,
時, >0, 即
>0, 即 在
在 上單調遞增,故
上單調遞增,故 在
在 上的最大值為f(1)=a 因此a=1/2.
上的最大值為f(1)=a 因此a=1/2.
某跨國飲料公司對全世界所有人均GDP(即人均純收入)在0.5-8千美元的地區銷售該公司A飲料的情況的調查中發現:人均GDP處在中等的地區對該飲料的銷售量最多,然后向兩邊遞減。
(Ⅰ)下列幾個模擬函數中(x表示人均GDP,單位:千美元,y表示年人均A飲料的銷量,單位;升),用哪個來描述人均A飲料銷量與地區的人均GDP的關系更合適?說明理由。
①![]() , ②
, ②![]() , ③
, ③![]() , ④
, ④![]()
(Ⅱ)若人均GDP為1千美元時,年人均A飲料的銷量為2升;若人均GDP為4千美元時,年人均A飲料的銷量為5升,把(Ⅰ)中你所選的模擬函數求出來,并求在各個地區中,年人均A飲料的銷量最多是多少?
(Ⅲ)因為A飲料在B國被檢測出殺蟲劑的含量超標,受此事件的影響,A飲料在人均GDP低于3千美元和高于6千美元的地區銷量下降5%,其它地區的銷量下降10%,根據(Ⅱ)所求出的模擬函數,求在各個地區中,年人均A飲料的銷量最多為多少?
某跨國飲料公司在對全世界所有人均GDP(即人均純收入)在0.5千美元~8千美元的地區銷售該公司![]() 飲料的情況的調查中發現:人均GDP處在中等的地區對該飲料的銷售量最多,然后向兩邊遞減。
飲料的情況的調查中發現:人均GDP處在中等的地區對該飲料的銷售量最多,然后向兩邊遞減。
(1)下列幾個模擬函數中![]() 表示人均GDP,單位:千美元,
表示人均GDP,單位:千美元,![]() 表示年人均
表示年人均![]() 飲料的銷量,單位:升),用哪個模擬函數來描述人均
飲料的銷量,單位:升),用哪個模擬函數來描述人均![]() 飲料銷量與地區的人均
飲料銷量與地區的人均![]() 關系更合適?說明理由。①
關系更合適?說明理由。①![]() ②
②![]() ,③
,③![]() ,④
,④![]() 。
。
(2)若人均GDP為1千美元時,年人均![]() 飲料的銷量為2升;若人均GDP為4千美元時,年人均
飲料的銷量為2升;若人均GDP為4千美元時,年人均![]() 飲料的銷量為5升,把(1)中你所選的模擬函數求出來,并求出各個地區中,年人均
飲料的銷量為5升,把(1)中你所選的模擬函數求出來,并求出各個地區中,年人均![]() 飲料的銷量最多是多少?
飲料的銷量最多是多少?
設函數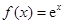 ,其中
,其中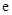 為自然對數的底數.
為自然對數的底數.
(1)求函數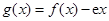 的單調區間;
的單調區間;
(2)記曲線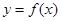 在點
在點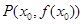 (其中
(其中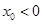 )處的切線為
)處的切線為 ,
, 與
與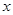 軸、
軸、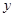 軸所圍成的三角形面積為
軸所圍成的三角形面積為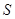 ,求
,求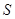 的最大值.
的最大值.
【解析】第一問利用由已知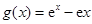 ,所以
,所以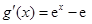 ,
,
由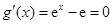 ,得
,得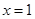 ,
所以,在區間
,
所以,在區間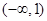 上,
上,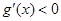 ,函數
,函數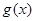 在區間
在區間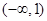 上單調遞減;
在區間
上單調遞減;
在區間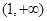 上,
上, ,函數
,函數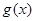 在區間
在區間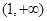 上單調遞增;
上單調遞增;
第二問中,因為 ,所以曲線
,所以曲線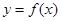 在點
在點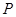 處切線為
處切線為 :
: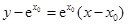 .
.
切線 與
與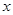 軸的交點為
軸的交點為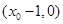 ,與
,與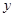 軸的交點為
軸的交點為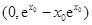 ,
,
因為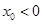 ,所以
,所以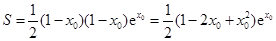 ,
,
 , 在區間
, 在區間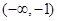 上,函數
上,函數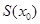 單調遞增,在區間
單調遞增,在區間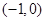 上,函數
上,函數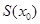 單調遞減.所以,當
單調遞減.所以,當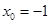 時,
時,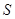 有最大值,此時
有最大值,此時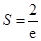 ,
,
解:(Ⅰ)由已知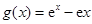 ,所以
,所以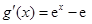 ,
由
,
由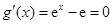 ,得
,得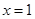 , 所以,在區間
, 所以,在區間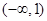 上,
上,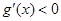 ,函數
,函數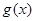 在區間
在區間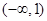 上單調遞減;
上單調遞減;
在區間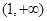 上,
上, ,函數
,函數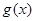 在區間
在區間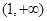 上單調遞增;
上單調遞增;
即函數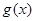 的單調遞減區間為
的單調遞減區間為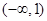 ,單調遞增區間為
,單調遞增區間為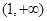 .
.
(Ⅱ)因為 ,所以曲線
,所以曲線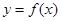 在點
在點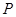 處切線為
處切線為 :
: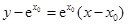 .
.
切線 與
與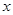 軸的交點為
軸的交點為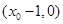 ,與
,與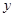 軸的交點為
軸的交點為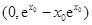 ,
,
因為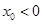 ,所以
,所以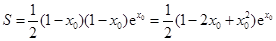 ,
,
 , 在區間
, 在區間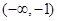 上,函數
上,函數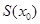 單調遞增,在區間
單調遞增,在區間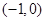 上,函數
上,函數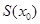 單調遞減.所以,當
單調遞減.所以,當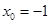 時,
時,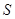 有最大值,此時
有最大值,此時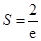 ,
,
所以,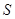 的最大值為
的最大值為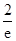
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com