
題目列表(包括答案和解析)
在三棱柱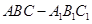 中,
中,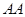
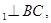
 ,
,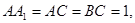
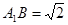
⑴求證:平面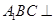 平面
平面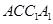 ;
;
⑵如果D為AB的中點,求證: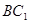 ∥平面
∥平面

如圖,在三棱柱![]() 中,
中,![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ,
,![]() 為
為![]() 的中點,且
的中點,且![]() ⊥
⊥![]() .
.
(1)求證:![]() ⊥平面
⊥平面![]() ;(2)求三棱錐
;(2)求三棱錐![]() 的體積.
的體積.
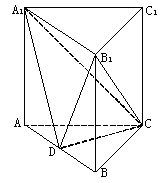
如圖,在三棱柱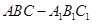 中,
中,  ,
, ,
,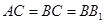 ,點
,點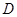 是
是 的中點,
的中點,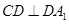 .
.

(Ⅰ)求證: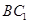 ∥平面
∥平面 ;
;
(Ⅱ)設點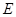 在線段
在線段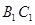 上,
上,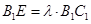 ,且使直線
,且使直線 和平面
和平面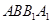 所成的角的正弦值為
所成的角的正弦值為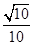 ,求
,求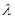 的值.
的值.
在三棱柱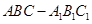 中,各側面均為正方形,側面
中,各側面均為正方形,側面 的對角線相交于點
的對角線相交于點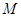 ,則
,則 與平面
與平面 所成角的大小是( )
所成角的大小是( )
A.30° B.45° C.60° D.90
在三棱柱 中,底面是正三角形,側棱
中,底面是正三角形,側棱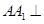 底面
底面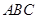 ,點
,點 是側面
是側面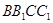 的中心,若
的中心,若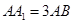 ,則直線
,則直線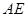 與平面
與平面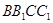 所成角的大小為( )
所成角的大小為( )
A.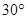 B.
B. C.
C.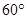 D.
D.
一、選擇題:每小題5分,滿分60分.
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
A
A
A
A
B
D
D
B
C
C
二、填空題:每小題5分,滿分20分.
13..files/image246.gif)
14. .files/image101.gif)
15..files/image249.gif)
16.①③④
.files/image250.gif) 三、解答題
三、解答題
17.設兩個實數為a,b,.files/image252.gif) ,
,.files/image254.gif) ,建立平面直角坐標系aOb, 則點
,建立平面直角坐標系aOb, 則點.files/image256.gif) 在正方形OABC內 ……… 2分
在正方形OABC內 ……… 2分
(Ⅰ) 記事件A“兩數之和小于.files/image258.gif) ,則滿足條件的點
,則滿足條件的點.files/image256.gif) 在多邊形OAEFC內
在多邊形OAEFC內
所以.files/image260.gif) ……… 6分
……… 6分
(Ⅱ) 記事件B“兩數的平方和小于.files/image256.gif) 在扇形內
在扇形內
所以.files/image262.gif) ………10分
………10分
18.∵m?n.files/image264.gif) ∴
∴.files/image266.gif) ……… 4分
……… 4分
再由余弦定理.files/image268.gif) 得:
得:.files/image270.gif)
(Ⅰ)由.files/image162.gif) 得
得.files/image272.gif) ,故
,故.files/image274.gif) ……… 8分
……… 8分
(Ⅱ)由.files/image270.gif) 得
得.files/image276.gif)
解得.files/image278.gif) ,所以
,所以.files/image164.gif) 的取值范圍是
的取值范圍是.files/image280.gif) ………12分
………12分
19.(Ⅰ)連接.files/image282.gif) ,交
,交.files/image284.gif) 于
于.files/image121.gif) ,易知
,易知.files/image121.gif) 為
為.files/image282.gif) 、
、.files/image284.gif) 中點,故在△
中點,故在△.files/image289.gif) 中,
中,.files/image291.gif) 為邊
為邊.files/image185.gif) 的中位線,故
的中位線,故.files/image185.gif) ∥
∥.files/image291.gif) ,
,.files/image295.gif) 平面
平面.files/image181.gif) ,
,.files/image297.gif) 平面
平面.files/image181.gif) ,所以
,所以.files/image185.gif) ∥平面
∥平面.files/image181.gif) ……… 5分
……… 5分
(Ⅱ)在平面.files/image183.gif) 內過點
內過點.files/image299.gif) 作
作.files/image301.gif) ⊥
⊥.files/image303.gif) ,垂足為H,
,垂足為H,
∵平面.files/image181.gif) ⊥平面
⊥平面.files/image183.gif) ,且平面
,且平面.files/image181.gif) ∩平面
∩平面.files/image183.gif)
.files/image305.gif) ,
,
∴.files/image301.gif) ⊥平面
⊥平面.files/image181.gif) ,∴
,∴.files/image301.gif) ⊥
⊥.files/image307.gif) , ……… 8分
, ……… 8分
又∵.files/image309.gif) ,
,.files/image177.gif) 為
為.files/image179.gif) 中點,∴
中點,∴.files/image179.gif) ⊥
⊥.files/image307.gif)
∴.files/image307.gif) ⊥平面
⊥平面.files/image183.gif) ,∴
,∴.files/image307.gif) ⊥
⊥.files/image314.gif) ,又∵
,又∵.files/image173.gif) ,
,
∴.files/image187.gif) ⊥平面
⊥平面.files/image150.gif) . ………12分
. ………12分
20.(Ⅰ)∵.files/image065.gif) 是各項均為正數的等差數列,且公差
是各項均為正數的等差數列,且公差.files/image196.gif)
∴.files/image316.gif) ∴
∴.files/image318.gif) ……… 3分
……… 3分
∴.files/image320.gif) 為常數,∴
為常數,∴.files/image198.gif) 是等差數列 ……… 5分
是等差數列 ……… 5分
(Ⅱ)∵.files/image322.gif) ,∴
,∴.files/image324.gif)
∴.files/image326.gif) 是公差為1的等差數列 ……… 7分
是公差為1的等差數列 ……… 7分
∴.files/image328.gif) ,∴
,∴.files/image330.gif) ……… 9分
……… 9分
當.files/image332.gif) 時,
時,.files/image334.gif) ………10分
………10分
當.files/image336.gif) 時,
時,.files/image338.gif)
綜上,.files/image340.gif) ………12分
………12分
21.(Ⅰ).files/image342.gif) ……… 4分
……… 4分
(Ⅱ)由橢圓的對稱性知:PRQS為菱形,原點O到各邊距離相等……… 5分
⑴當P在y軸上時,易知R在x軸上,此時PR方程為.files/image344.gif) ,
,
.files/image346.gif)
.files/image223.gif) . ……… 6分
. ……… 6分
⑵當P在x軸上時,易知R在y軸上,此時PR方程為.files/image344.gif) ,
,
.files/image346.gif)
.files/image223.gif) . ……… 7分
. ……… 7分
⑶當P不在坐標軸上時,設PQ斜率為k,.files/image348.gif) 、
、.files/image350.gif)
P在橢圓上,.files/image352.gif) .......①;R在橢圓上,
.......①;R在橢圓上,.files/image354.gif) ......②
......②
利用Rt△POR可得 .files/image356.gif) ……… 9分
……… 9分
即 .files/image358.gif)
整理得 .files/image360.gif) . ………11分
. ………11分
再將①②帶入,得.files/image223.gif)
綜上當.files/image221.gif) 時,有
時,有.files/image223.gif) . ………12分
. ………12分
22.(Ⅰ)∵.files/image362.gif) ,且
,且.files/image233.gif) ,∴
,∴.files/image364.gif)
∴在.files/image366.gif) 上,
上, .files/image368.gif) 和
和.files/image370.gif) 變化情況如下表:
變化情況如下表:
x
.files/image372.gif)
.files/image374.gif)
0
.files/image376.gif)
1
.files/image368.gif)
+
0
-
.files/image370.gif)
.files/image378.gif)
↑
b
↓
.files/image380.gif)
……… 2分
∵函數.files/image225.gif) 在
在.files/image236.gif) 上的最大值為1,
上的最大值為1,
∴.files/image382.gif) ,此時應有
,此時應有.files/image384.gif) ∴
∴.files/image386.gif)
∴.files/image386.gif) ,
,.files/image382.gif) ……… 4分
……… 4分
(Ⅱ).files/image390.gif) ……… 6分
……… 6分
所求切線方程為.files/image392.gif) ………
8分
………
8分
(Ⅲ).files/image394.gif) ………10分
………10分
設.files/image396.gif)
△.files/image398.gif)
∴當.files/image400.gif) 時,函數
時,函數.files/image244.gif) 的無極值點
的無極值點
當.files/image402.gif) 時,函數
時,函數.files/image244.gif) 有兩個極值點 ………12分
有兩個極值點 ………12分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com