
題目列表(包括答案和解析)
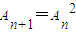 ,則稱數(shù)列{An}為“平方遞推數(shù)列”.已知數(shù)列{an}中,a1=2,點(diǎn)(an,an+1)在函數(shù)f(x)=2x2+2x的圖象上,其中n為正整數(shù).
,則稱數(shù)列{An}為“平方遞推數(shù)列”.已知數(shù)列{an}中,a1=2,點(diǎn)(an,an+1)在函數(shù)f(x)=2x2+2x的圖象上,其中n為正整數(shù).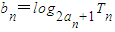 ,求數(shù)列{bn}的前n項(xiàng)和Sn.
,求數(shù)列{bn}的前n項(xiàng)和Sn.在各項(xiàng)均為正數(shù)的數(shù)列![]() 中,前
中,前![]() 項(xiàng)和
項(xiàng)和![]() 滿足
滿足![]() 。
。
(1)證明![]() 是等差數(shù)列,并求這個數(shù)列的通項(xiàng)公式及前
是等差數(shù)列,并求這個數(shù)列的通項(xiàng)公式及前![]() 項(xiàng)和的公式;
項(xiàng)和的公式;
(2)在平面直角坐標(biāo)系![]() 面上,設(shè)點(diǎn)
面上,設(shè)點(diǎn)![]() 滿足
滿足![]() ,且點(diǎn)
,且點(diǎn)![]() 在直線
在直線![]() 上,
上,![]() 中最高點(diǎn)為
中最高點(diǎn)為![]() ,若稱直線
,若稱直線![]() 與
與![]() 軸、直線
軸、直線![]() 所圍成的圖形的面積為直線
所圍成的圖形的面積為直線![]() 在區(qū)間
在區(qū)間![]() 上的面積,試求直線
上的面積,試求直線![]() 在區(qū)間
在區(qū)間![]() 上的面積;
上的面積;
(3)若存在圓心在直線![]() 上的圓紙片能覆蓋住點(diǎn)列
上的圓紙片能覆蓋住點(diǎn)列![]() 中任何一個點(diǎn),求該圓紙片最小面積.
中任何一個點(diǎn),求該圓紙片最小面積.
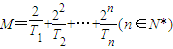 ,求證:
,求證: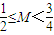 .
.1. {2,8} 2. 測卷數(shù)學(xué)試題.files/image262.gif) 3.
3. 測卷數(shù)學(xué)試題.files/image264.gif) 4.
4. 測卷數(shù)學(xué)試題.files/image266.gif)
5. 測卷數(shù)學(xué)試題.files/image268.gif)
測卷數(shù)學(xué)試題.files/image270.gif) 6. 1 7.20
6. 1 7.20
8. 測卷數(shù)學(xué)試題.files/image272.gif) 9.
9. 測卷數(shù)學(xué)試題.files/image274.gif) 10.2
10.2
11.測卷數(shù)學(xué)試題.files/image276.gif) 12.
12. 測卷數(shù)學(xué)試題.files/image278.gif) 13. [2,3] 14.
13. [2,3] 14. 測卷數(shù)學(xué)試題.files/image280.gif)
15.證明:(Ⅰ)在測卷數(shù)學(xué)試題.files/image282.gif) 中,
中,
∵測卷數(shù)學(xué)試題.files/image133.gif) ,
,測卷數(shù)學(xué)試題.files/image285.gif) ,
,測卷數(shù)學(xué)試題.files/image287.gif) ,∴
,∴測卷數(shù)學(xué)試題.files/image289.gif) .
.
∴測卷數(shù)學(xué)試題.files/image291.gif) .????????????????? 2分
.????????????????? 2分
又 ∵平面測卷數(shù)學(xué)試題.files/image293.gif) 平面
平面測卷數(shù)學(xué)試題.files/image295.gif) ,
,
平面測卷數(shù)學(xué)試題.files/image297.gif) 平面
平面測卷數(shù)學(xué)試題.files/image299.gif) ,
,測卷數(shù)學(xué)試題.files/image301.gif) 平面
平面測卷數(shù)學(xué)試題.files/image295.gif) ,
,
∴測卷數(shù)學(xué)試題.files/image304.gif) 平面
平面測卷數(shù)學(xué)試題.files/image306.gif) .
.
又測卷數(shù)學(xué)試題.files/image301.gif) 平面
平面測卷數(shù)學(xué)試題.files/image309.gif) ,
,
∴平面測卷數(shù)學(xué)試題.files/image311.gif) 平面
平面測卷數(shù)學(xué)試題.files/image306.gif) .………………………………………………………………4分
.………………………………………………………………4分
(Ⅱ)當(dāng)測卷數(shù)學(xué)試題.files/image139.gif) 點(diǎn)位于線段PC靠近C點(diǎn)的三等分點(diǎn)處時,
點(diǎn)位于線段PC靠近C點(diǎn)的三等分點(diǎn)處時,測卷數(shù)學(xué)試題.files/image315.gif) 平面
平面測卷數(shù)學(xué)試題.files/image317.gif) .………5分
.………5分
證明如下:連接AC,交測卷數(shù)學(xué)試題.files/image319.gif) 于點(diǎn)N,連接MN.
于點(diǎn)N,連接MN.
∵測卷數(shù)學(xué)試題.files/image321.gif) ,所以四邊形
,所以四邊形測卷數(shù)學(xué)試題.files/image295.gif) 是梯形.
是梯形.
∵測卷數(shù)學(xué)試題.files/image324.gif) ,∴
,∴測卷數(shù)學(xué)試題.files/image326.gif) .
.
又 ∵測卷數(shù)學(xué)試題.files/image328.gif) ,
,
∴測卷數(shù)學(xué)試題.files/image330.gif)
測卷數(shù)學(xué)試題.files/image332.gif) ,∴
,∴測卷數(shù)學(xué)試題.files/image315.gif) MN.…………………………………………………7分
MN.…………………………………………………7分
∵測卷數(shù)學(xué)試題.files/image334.gif) 平面
平面測卷數(shù)學(xué)試題.files/image309.gif) ,∴
,∴測卷數(shù)學(xué)試題.files/image315.gif) 平面
平面測卷數(shù)學(xué)試題.files/image317.gif) .………………………………………9分
.………………………………………9分
(Ⅲ)過測卷數(shù)學(xué)試題.files/image336.gif) 作
作測卷數(shù)學(xué)試題.files/image338.gif) 交
交測卷數(shù)學(xué)試題.files/image340.gif) 于
于測卷數(shù)學(xué)試題.files/image342.gif) ,
,
∵平面測卷數(shù)學(xué)試題.files/image293.gif) 平面
平面測卷數(shù)學(xué)試題.files/image295.gif) ,
,
∴測卷數(shù)學(xué)試題.files/image346.gif) 平面
平面測卷數(shù)學(xué)試題.files/image295.gif) .
.
即測卷數(shù)學(xué)試題.files/image349.gif) 為四棱錐
為四棱錐測卷數(shù)學(xué)試題.files/image351.gif) 的高.……………………………………………………11分
的高.……………………………………………………11分
又 ∵測卷數(shù)學(xué)試題.files/image353.gif) 是邊長為4的等邊三角形,∴
是邊長為4的等邊三角形,∴測卷數(shù)學(xué)試題.files/image355.gif) .……………12分
.……………12分
測卷數(shù)學(xué)試題.files/image357.gif) 在
在測卷數(shù)學(xué)試題.files/image359.gif) 中,斜邊
中,斜邊測卷數(shù)學(xué)試題.files/image361.gif) 邊上的高為
邊上的高為測卷數(shù)學(xué)試題.files/image363.gif) ,此即為梯形
,此即為梯形測卷數(shù)學(xué)試題.files/image295.gif) 的高.
的高.
∴梯形測卷數(shù)學(xué)試題.files/image295.gif) 的面積
的面積測卷數(shù)學(xué)試題.files/image366.gif) .
.
故測卷數(shù)學(xué)試題.files/image368.gif) .……………………………………………14分
.……………………………………………14分
16.設(shè)測卷數(shù)學(xué)試題.files/image152.gif) 的二次項(xiàng)系數(shù)為
的二次項(xiàng)系數(shù)為測卷數(shù)學(xué)試題.files/image371.gif) ,其圖象上兩點(diǎn)為(
,其圖象上兩點(diǎn)為(測卷數(shù)學(xué)試題.files/image373.gif) ,
,測卷數(shù)學(xué)試題.files/image375.gif) )、B(
)、B(測卷數(shù)學(xué)試題.files/image377.gif) ,
,測卷數(shù)學(xué)試題.files/image379.gif) )因?yàn)?sub>
)因?yàn)?sub>測卷數(shù)學(xué)試題.files/image381.gif) ,
,測卷數(shù)學(xué)試題.files/image156.gif) ,所以
,所以測卷數(shù)學(xué)試題.files/image384.gif) ,由x的任意性得f(x)的圖象關(guān)于直線x=1對稱, ………………………………………………………………(2分)
,由x的任意性得f(x)的圖象關(guān)于直線x=1對稱, ………………………………………………………………(2分)
∵ 測卷數(shù)學(xué)試題.files/image386.gif) ,
,測卷數(shù)學(xué)試題.files/image388.gif) ,
,測卷數(shù)學(xué)試題.files/image390.gif) ,
,
測卷數(shù)學(xué)試題.files/image392.gif) ,
,測卷數(shù)學(xué)試題.files/image394.gif) ,
,測卷數(shù)學(xué)試題.files/image396.gif)
測卷數(shù)學(xué)試題.files/image398.gif) ,………………………………(4分)
,………………………………(4分)
∴ 當(dāng)測卷數(shù)學(xué)試題.files/image400.gif) 時,∵f(x)在x≥1內(nèi)是增函數(shù),
時,∵f(x)在x≥1內(nèi)是增函數(shù),
測卷數(shù)學(xué)試題.files/image402.gif)
測卷數(shù)學(xué)試題.files/image404.gif)
測卷數(shù)學(xué)試題.files/image406.gif)
測卷數(shù)學(xué)試題.files/image408.gif)
測卷數(shù)學(xué)試題.files/image410.gif)
測卷數(shù)學(xué)試題.files/image412.gif) ,
,測卷數(shù)學(xué)試題.files/image414.gif) .
.
∵ 測卷數(shù)學(xué)試題.files/image416.gif) , ∴
, ∴ 測卷數(shù)學(xué)試題.files/image418.gif) .………………………………………………(8分)
.………………………………………………(8分)
當(dāng)測卷數(shù)學(xué)試題.files/image420.gif) 時,∵f(x)在x≥1內(nèi)是減函數(shù).
時,∵f(x)在x≥1內(nèi)是減函數(shù).
同理可得測卷數(shù)學(xué)試題.files/image422.gif) 或
或測卷數(shù)學(xué)試題.files/image424.gif) ,
,測卷數(shù)學(xué)試題.files/image414.gif) .………………………………………(11分)
.………………………………………(11分)
綜上:測卷數(shù)學(xué)試題.files/image426.gif) 的解集是當(dāng)
的解集是當(dāng)測卷數(shù)學(xué)試題.files/image400.gif) 時,為
時,為測卷數(shù)學(xué)試題.files/image429.gif)
當(dāng)測卷數(shù)學(xué)試題.files/image420.gif) 時,為
時,為測卷數(shù)學(xué)試題.files/image432.gif) ,或
,或測卷數(shù)學(xué)試題.files/image434.gif) .
.
17.解:(1)若測卷數(shù)學(xué)試題.files/image436.gif) 千米/小時,每小時耗油量為
千米/小時,每小時耗油量為測卷數(shù)學(xué)試題.files/image438.gif) 升/小時. 共耗油
升/小時. 共耗油測卷數(shù)學(xué)試題.files/image440.gif) 升.
升.
所以,從甲地到乙地要耗油
(2)設(shè)當(dāng)汽車以測卷數(shù)學(xué)試題.files/image034.gif) 千米/小時的速度勻速行駛時耗油量最少,
千米/小時的速度勻速行駛時耗油量最少,測卷數(shù)學(xué)試題.files/image443.gif) ,耗油量為S升.
,耗油量為S升.
則測卷數(shù)學(xué)試題.files/image445.gif) ,
,
測卷數(shù)學(xué)試題.files/image447.gif) ,
,
令測卷數(shù)學(xué)試題.files/image449.gif) ,解得,
,解得,測卷數(shù)學(xué)試題.files/image451.gif) .
.
列表:
測卷數(shù)學(xué)試題.files/image034.gif)
測卷數(shù)學(xué)試題.files/image454.gif)
測卷數(shù)學(xué)試題.files/image456.gif)
測卷數(shù)學(xué)試題.files/image458.gif)
測卷數(shù)學(xué)試題.files/image460.gif)
測卷數(shù)學(xué)試題.files/image462.gif)
測卷數(shù)學(xué)試題.files/image464.gif)
測卷數(shù)學(xué)試題.files/image466.gif)
測卷數(shù)學(xué)試題.files/image468.gif)
測卷數(shù)學(xué)試題.files/image466.gif)
測卷數(shù)學(xué)試題.files/image471.gif)
單調(diào)減
極小值11.25
單調(diào)增
測卷數(shù)學(xué)試題.files/image473.gif)
所以,當(dāng)汽車以
18.解:(Ⅰ)設(shè)測卷數(shù)學(xué)試題.files/image475.gif)
測卷數(shù)學(xué)試題.files/image477.gif)
對稱軸方程測卷數(shù)學(xué)試題.files/image479.gif) ,由題意
,由題意測卷數(shù)學(xué)試題.files/image481.gif) 或
或測卷數(shù)學(xué)試題.files/image483.gif) 或
或測卷數(shù)學(xué)試題.files/image485.gif)
∴測卷數(shù)學(xué)試題.files/image487.gif) 或
或測卷數(shù)學(xué)試題.files/image489.gif) 或
或測卷數(shù)學(xué)試題.files/image491.gif) ∴
∴測卷數(shù)學(xué)試題.files/image493.gif)
(Ⅱ)由已知與(Ⅰ)得:測卷數(shù)學(xué)試題.files/image495.gif) ,
,測卷數(shù)學(xué)試題.files/image497.gif) ,
,
測卷數(shù)學(xué)試題.files/image499.gif) ,
,測卷數(shù)學(xué)試題.files/image501.gif) ,
,測卷數(shù)學(xué)試題.files/image503.gif) .
.
測卷數(shù)學(xué)試題.files/image505.gif) 橢圓的標(biāo)準(zhǔn)方程為
橢圓的標(biāo)準(zhǔn)方程為測卷數(shù)學(xué)試題.files/image507.gif) .
.
設(shè)測卷數(shù)學(xué)試題.files/image509.gif) ,
,測卷數(shù)學(xué)試題.files/image511.gif) ,聯(lián)立
,聯(lián)立測卷數(shù)學(xué)試題.files/image513.gif)
得測卷數(shù)學(xué)試題.files/image515.gif) ,
,
測卷數(shù)學(xué)試題.files/image517.gif)
又測卷數(shù)學(xué)試題.files/image519.gif) ,
,
因?yàn)闄E圓的右頂點(diǎn)為測卷數(shù)學(xué)試題.files/image521.gif) ,
,測卷數(shù)學(xué)試題.files/image523.gif) ,即
,即測卷數(shù)學(xué)試題.files/image525.gif) ,
,
測卷數(shù)學(xué)試題.files/image527.gif) ,
,
測卷數(shù)學(xué)試題.files/image529.gif) ,
,測卷數(shù)學(xué)試題.files/image531.gif) .
.
解得:測卷數(shù)學(xué)試題.files/image533.gif) ,
,測卷數(shù)學(xué)試題.files/image535.gif) ,且均滿足
,且均滿足測卷數(shù)學(xué)試題.files/image537.gif) ,
,
當(dāng)測卷數(shù)學(xué)試題.files/image533.gif) 時,
時,測卷數(shù)學(xué)試題.files/image214.gif) 的方程為
的方程為測卷數(shù)學(xué)試題.files/image541.gif) ,直線過定點(diǎn)
,直線過定點(diǎn)測卷數(shù)學(xué)試題.files/image543.gif) ,與已知矛盾;
,與已知矛盾;
當(dāng)測卷數(shù)學(xué)試題.files/image535.gif) 時,
時,測卷數(shù)學(xué)試題.files/image214.gif) 的方程為
的方程為測卷數(shù)學(xué)試題.files/image547.gif) ,直線過定點(diǎn)
,直線過定點(diǎn)測卷數(shù)學(xué)試題.files/image549.gif) .
.
所以,直線測卷數(shù)學(xué)試題.files/image214.gif) 過定點(diǎn),定點(diǎn)坐標(biāo)為
過定點(diǎn),定點(diǎn)坐標(biāo)為測卷數(shù)學(xué)試題.files/image549.gif) .
.
19. 解: (1) 由題知: 測卷數(shù)學(xué)試題.files/image553.gif) , 解得
, 解得測卷數(shù)學(xué)試題.files/image555.gif) , 故
, 故測卷數(shù)學(xué)試題.files/image557.gif) .
.
(2) 測卷數(shù)學(xué)試題.files/image559.gif) ,
,
測卷數(shù)學(xué)試題.files/image561.gif) ,
,
測卷數(shù)學(xué)試題.files/image563.gif) ,
,
又測卷數(shù)學(xué)試題.files/image565.gif) 滿足上式. 所以
滿足上式. 所以測卷數(shù)學(xué)試題.files/image567.gif) .
.
(3) 若測卷數(shù)學(xué)試題.files/image231.gif) 是
是測卷數(shù)學(xué)試題.files/image233.gif) 與
與測卷數(shù)學(xué)試題.files/image235.gif) 的等差中項(xiàng), 則
的等差中項(xiàng), 則測卷數(shù)學(xué)試題.files/image569.gif) ,
,
從而測卷數(shù)學(xué)試題.files/image571.gif) , 得
, 得測卷數(shù)學(xué)試題.files/image573.gif) .
.
因?yàn)?sub>測卷數(shù)學(xué)試題.files/image567.gif) 是
是測卷數(shù)學(xué)試題.files/image061.gif) 的減函數(shù), 所以
的減函數(shù), 所以
當(dāng)測卷數(shù)學(xué)試題.files/image576.gif) , 即
, 即測卷數(shù)學(xué)試題.files/image578.gif) 時,
時, 測卷數(shù)學(xué)試題.files/image233.gif) 隨
隨測卷數(shù)學(xué)試題.files/image061.gif) 的增大而減小, 此時最小值為
的增大而減小, 此時最小值為測卷數(shù)學(xué)試題.files/image582.gif) ;
;
當(dāng)測卷數(shù)學(xué)試題.files/image584.gif) , 即
, 即測卷數(shù)學(xué)試題.files/image586.gif) 時,
時, 測卷數(shù)學(xué)試題.files/image233.gif) 隨
隨測卷數(shù)學(xué)試題.files/image061.gif) 的增大而增大, 此時最小值為
的增大而增大, 此時最小值為測卷數(shù)學(xué)試題.files/image588.gif) .
.
又測卷數(shù)學(xué)試題.files/image590.gif) , 所以
, 所以測卷數(shù)學(xué)試題.files/image592.gif) ,
,
即數(shù)列測卷數(shù)學(xué)試題.files/image237.gif) 中
中測卷數(shù)學(xué)試題.files/image582.gif) 最小, 且
最小, 且測卷數(shù)學(xué)試題.files/image596.gif) .
.
20. 解:(1)由題意得測卷數(shù)學(xué)試題.files/image598.gif)
測卷數(shù)學(xué)試題.files/image600.gif)
而測卷數(shù)學(xué)試題.files/image602.gif) ,所以
,所以測卷數(shù)學(xué)試題.files/image245.gif) 、
、測卷數(shù)學(xué)試題.files/image247.gif) 的關(guān)系為
的關(guān)系為測卷數(shù)學(xué)試題.files/image606.gif)
(2)由(1)知測卷數(shù)學(xué)試題.files/image608.gif) ,
,
測卷數(shù)學(xué)試題.files/image610.gif)
令測卷數(shù)學(xué)試題.files/image612.gif) ,要使
,要使測卷數(shù)學(xué)試題.files/image152.gif) 在其定義域
在其定義域測卷數(shù)學(xué)試題.files/image615.gif) 內(nèi)是單調(diào)函數(shù),只需
內(nèi)是單調(diào)函數(shù),只需測卷數(shù)學(xué)試題.files/image617.gif) 在
在測卷數(shù)學(xué)試題.files/image615.gif) 內(nèi)滿足:
內(nèi)滿足:測卷數(shù)學(xué)試題.files/image619.gif) 恒成立.
恒成立.
①當(dāng)測卷數(shù)學(xué)試題.files/image621.gif) 時,
時,測卷數(shù)學(xué)試題.files/image623.gif) ,因?yàn)?sub>
,因?yàn)?sub>測卷數(shù)學(xué)試題.files/image034.gif) >
>測卷數(shù)學(xué)試題.files/image466.gif) ,所以
,所以測卷數(shù)學(xué)試題.files/image617.gif) <0,
<0,測卷數(shù)學(xué)試題.files/image628.gif) <0,
<0,
∴測卷數(shù)學(xué)試題.files/image152.gif) 在
在測卷數(shù)學(xué)試題.files/image615.gif) 內(nèi)是單調(diào)遞減函數(shù),即
內(nèi)是單調(diào)遞減函數(shù),即測卷數(shù)學(xué)試題.files/image621.gif) 適合題意;
適合題意;
②當(dāng)測卷數(shù)學(xué)試題.files/image245.gif) >0時,
>0時,測卷數(shù)學(xué)試題.files/image612.gif) ,其圖像為開口向上的拋物線,對稱軸為
,其圖像為開口向上的拋物線,對稱軸為測卷數(shù)學(xué)試題.files/image632.gif) ,∴
,∴測卷數(shù)學(xué)試題.files/image634.gif) ,
,
只需測卷數(shù)學(xué)試題.files/image636.gif) ,即
,即測卷數(shù)學(xué)試題.files/image638.gif) ,
,
∴測卷數(shù)學(xué)試題.files/image152.gif) 在
在測卷數(shù)學(xué)試題.files/image615.gif) 內(nèi)為單調(diào)遞增函數(shù),故
內(nèi)為單調(diào)遞增函數(shù),故測卷數(shù)學(xué)試題.files/image640.gif) 適合題意.
適合題意.
③當(dāng)測卷數(shù)學(xué)試題.files/image245.gif) <0時,
<0時,測卷數(shù)學(xué)試題.files/image612.gif) ,其圖像為開口向下的拋物線,對稱軸為
,其圖像為開口向下的拋物線,對稱軸為測卷數(shù)學(xué)試題.files/image643.gif) ,只要
,只要測卷數(shù)學(xué)試題.files/image645.gif) ,即
,即測卷數(shù)學(xué)試題.files/image647.gif) 時,
時,測卷數(shù)學(xué)試題.files/image649.gif) 在
在測卷數(shù)學(xué)試題.files/image615.gif) 恒成立,故
恒成立,故測卷數(shù)學(xué)試題.files/image245.gif) <0適合題意.
<0適合題意.
綜上所述,測卷數(shù)學(xué)試題.files/image245.gif) 的取值范圍為
的取值范圍為測卷數(shù)學(xué)試題.files/image652.gif) .
.
(3)∵測卷數(shù)學(xué)試題.files/image251.gif) 在
在測卷數(shù)學(xué)試題.files/image253.gif) 上是減函數(shù),
上是減函數(shù),
∴測卷數(shù)學(xué)試題.files/image656.gif) 時,
時,測卷數(shù)學(xué)試題.files/image658.gif) ;
;測卷數(shù)學(xué)試題.files/image660.gif) 時,
時,測卷數(shù)學(xué)試題.files/image662.gif) ,即
,即測卷數(shù)學(xué)試題.files/image664.gif) ,
,
①當(dāng)測卷數(shù)學(xué)試題.files/image647.gif) 時,由(2)知
時,由(2)知測卷數(shù)學(xué)試題.files/image152.gif) 在
在測卷數(shù)學(xué)試題.files/image253.gif) 上遞減
上遞減測卷數(shù)學(xué)試題.files/image667.gif) <2,不合題意;
<2,不合題意;
②當(dāng)0<測卷數(shù)學(xué)試題.files/image245.gif) <1時,由
<1時,由測卷數(shù)學(xué)試題.files/image670.gif) ,
,
又由(2)知當(dāng)測卷數(shù)學(xué)試題.files/image672.gif) 時,
時,測卷數(shù)學(xué)試題.files/image152.gif) 在
在測卷數(shù)學(xué)試題.files/image253.gif) 上是增函數(shù),
上是增函數(shù),
∴測卷數(shù)學(xué)試題.files/image675.gif) <
<測卷數(shù)學(xué)試題.files/image677.gif) ,不合題意;
,不合題意;
③當(dāng)測卷數(shù)學(xué)試題.files/image640.gif) 時,由(2)知
時,由(2)知測卷數(shù)學(xué)試題.files/image152.gif) 在
在測卷數(shù)學(xué)試題.files/image253.gif) 上是增函數(shù),
上是增函數(shù),測卷數(shù)學(xué)試題.files/image680.gif) <2,又
<2,又測卷數(shù)學(xué)試題.files/image682.gif) 在
在測卷數(shù)學(xué)試題.files/image253.gif) 上是減函數(shù),
上是減函數(shù),
故只需測卷數(shù)學(xué)試題.files/image684.gif) >
>測卷數(shù)學(xué)試題.files/image686.gif) ,
,測卷數(shù)學(xué)試題.files/image688.gif) ,而
,而測卷數(shù)學(xué)試題.files/image690.gif) ,
,測卷數(shù)學(xué)試題.files/image658.gif)
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com