
題目列表(包括答案和解析)
用數學歸納法證明:
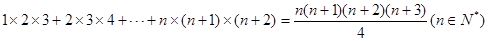 .
.
【解析】首先證明當n=1時等式成立,再假設n=k時等式成立,得到等式
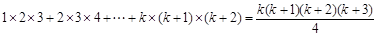 ,
,
下面證明當n=k+1時等式左邊
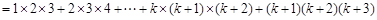 ,
,
根據前面的假設化簡即可得到結果,最后得到結論.
已知函數f(x)=ex-ax,其中a>0.
(1)若對一切x∈R,f(x)  1恒成立,求a的取值集合;
1恒成立,求a的取值集合;
(2)在函數f(x)的圖像上去定點A(x1, f(x1)),B(x2, f(x2))(x1<x2),記直線AB的斜率為k,證明:存在x0∈(x1,x2),使 恒成立.
恒成立.
【解析】解: 令
令 .
.
當 時
時 單調遞減;當
單調遞減;當 時
時 單調遞增,故當
單調遞增,故當 時,
時, 取最小值
取最小值
于是對一切 恒成立,當且僅當
恒成立,當且僅當 . ①
. ①
令 則
則
當 時,
時, 單調遞增;當
單調遞增;當 時,
時, 單調遞減.
單調遞減.
故當 時,
時, 取最大值
取最大值 .因此,當且僅當
.因此,當且僅當 時,①式成立.
時,①式成立.
綜上所述, 的取值集合為
的取值集合為 .
.
(Ⅱ)由題意知, 令
令 則
則


令 ,則
,則 .當
.當 時,
時, 單調遞減;當
單調遞減;當 時,
時, 單調遞增.故當
單調遞增.故當 ,
, 即
即
從而 ,
, 又
又

所以
 因為函數
因為函數 在區間
在區間 上的圖像是連續不斷的一條曲線,所以存在
上的圖像是連續不斷的一條曲線,所以存在 使
使 即
即 成立.
成立.
【點評】本題考查利用導函數研究函數單調性、最值、不等式恒成立問題等,考查運算能力,考查分類討論思想、函數與方程思想等數學方法.第一問利用導函數法求出 取最小值
取最小值 對一切x∈R,f(x)
對一切x∈R,f(x)  1恒成立轉化為
1恒成立轉化為 從而得出求a的取值集合;第二問在假設存在的情況下進行推理,然后把問題歸結為一個方程是否存在解的問題,通過構造函數,研究這個函數的性質進行分析判斷.
從而得出求a的取值集合;第二問在假設存在的情況下進行推理,然后把問題歸結為一個方程是否存在解的問題,通過構造函數,研究這個函數的性質進行分析判斷.
已知 ,(其中
,(其中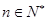 )
)
⑴求 及
及 ;
;
⑵試比較 與
與 的大小,并說明理由.
的大小,并說明理由.
【解析】第一問中取 ,則
,則 ;
…………1分
;
…………1分
對等式兩邊求導,得
取 ,則
,則 得到結論
得到結論
第二問中,要比較 與
與 的大小,即比較:
的大小,即比較: 與
與 的大小,歸納猜想可得結論當
的大小,歸納猜想可得結論當 時,
時, ;
;
當 時,
時, ;
;
當 時,
時, ;
;
猜想:當 時,
時, 運用數學歸納法證明即可。
運用數學歸納法證明即可。
解:⑴取 ,則
,則 ;
…………1分
;
…………1分
對等式兩邊求導,得 ,
,
取 ,則
,則 。 …………4分
。 …………4分
⑵要比較 與
與 的大小,即比較:
的大小,即比較: 與
與 的大小,
的大小,
當 時,
時, ;
;
當 時,
時, ;
;
當 時,
時, ;
…………6分
;
…………6分
猜想:當 時,
時, ,下面用數學歸納法證明:
,下面用數學歸納法證明:
由上述過程可知, 時結論成立,
時結論成立,
假設當 時結論成立,即
時結論成立,即 ,
,
當 時,
時,
而
∴
即 時結論也成立,
時結論也成立,
∴當 時,
時, 成立。
…………11分
成立。
…………11分
綜上得,當 時,
時, ;
;
當 時,
時, ;
;
當 時,
時,
在數列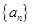 中,
中,
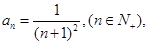 記
記
(Ⅰ)求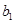 、
、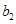 、
、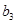 、
、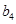 并推測
并推測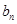 ;
;
(Ⅱ)用數學歸納法證明你的結論.
【解析】第一問利用遞推關系可知,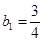 、
、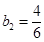 、
、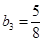 、
、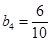 ,猜想可得
,猜想可得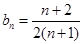
第二問中,①當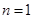 時,
時,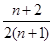 =
=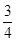 ,又
,又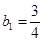 ,猜想正確
,猜想正確
②假設當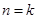 時猜想成立,即
時猜想成立,即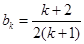 ,
,
當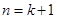 時,
時,
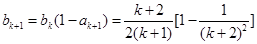 =
=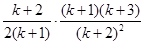
=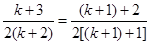 ,即當
,即當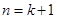 時猜想也成立
時猜想也成立
兩步驟得到。
(2)①當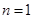 時,
時,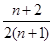 =
=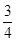 ,又
,又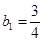 ,猜想正確
,猜想正確
②假設當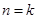 時猜想成立,即
時猜想成立,即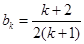 ,
,
當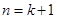 時,
時,
 =
=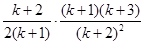
=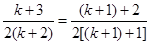 ,即當
,即當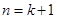 時猜想也成立
時猜想也成立
由①②可知,對于任何正整數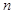 都有
都有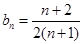 成立
成立
已知數列 的前
的前 項和為
項和為 ,且
,且 (
( N*),其中
N*),其中 .
.
(Ⅰ) 求 的通項公式;
的通項公式;
(Ⅱ) 設 (
( N*).
N*).
①證明:  ;
;
② 求證: .
.
【解析】本試題主要考查了數列的通項公式的求解和運用。運用 關系式,表示通項公式,然后得到第一問,第二問中利用放縮法得到
關系式,表示通項公式,然后得到第一問,第二問中利用放縮法得到 ,②由于
,②由于 ,
,
所以 利用放縮法,從此得到結論。
利用放縮法,從此得到結論。
解:(Ⅰ)當 時,由
時,由 得
得 . ……2分
. ……2分
若存在 由
由 得
得 ,
,
從而有 ,與
,與 矛盾,所以
矛盾,所以 .
.
從而由 得
得 得
得 . ……6分
. ……6分
(Ⅱ)①證明:
證法一:∵ ∴
∴
∴
∴ .…………10分
.…………10分
證法二: ,下同證法一.
……10分
,下同證法一.
……10分
證法三:(利用對偶式)設 ,
, ,
,
則 .又
.又 ,也即
,也即 ,所以
,所以 ,也即
,也即 ,又因為
,又因為 ,所以
,所以 .即
.即
 ………10分
………10分
證法四:(數學歸納法)①當 時,
時,  ,命題成立;
,命題成立;
②假設 時,命題成立,即
時,命題成立,即 ,
,
則當 時,
時,

 即
即
即
故當 時,命題成立.
時,命題成立.
綜上可知,對一切非零自然數 ,不等式②成立. ………………10分
,不等式②成立. ………………10分
②由于 ,
,
所以 ,
,
從而 .
.
也即
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com