
題目列表(包括答案和解析)
解:(1)OA=1,OC=2
則A點坐標為(0,1),C點坐標為(2,0)
設直線AC的解析式為y=kx+b
![]()
解得
![]() 直線AC的解析式為
直線AC的解析式為![]() ··················· 2分
··················· 2分
(2)![]() 或
或![]()
(正確一個得2分)························· 8分
 (3)如圖,設
(3)如圖,設![]()
過![]() 點作
點作![]() 于F
于F
![]()
由折疊知![]()
![]()
![]() 或2··········· 10分
或2··········· 10分
解:(1)由題意知,當![]() 、
、![]() 運動到
運動到![]() 秒時,如圖①,過
秒時,如圖①,過![]() 作
作![]() 交
交![]() 于
于![]() 點,則四邊形
點,則四邊形![]() 是平行四邊形.
是平行四邊形.
∵![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∴ ![]() .解得
.解得![]() . 5分
. 5分
(2)分三種情況討論:
① 當![]() 時,如圖②作
時,如圖②作![]() 交
交![]() 于
于![]() ,則有
,則有![]() 即.
即.
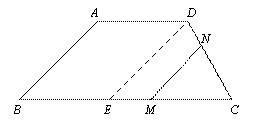 ∵
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() . 6分
. 6分
② 當![]() 時,如圖③,過
時,如圖③,過![]() 作
作![]() 于H.
于H.
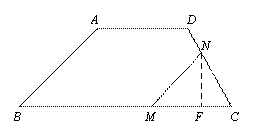 則
則![]() ,
,
∴![]() .
.
∴![]() .7分
.7分
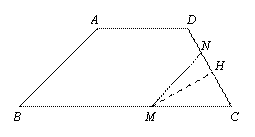
③ 當![]() 時,如圖④.
時,如圖④.
則![]() .
.
![]() . -------------------------------------8分
. -------------------------------------8分
綜上所述,當![]() 、
、![]() 或
或![]() 時,
時,![]() 為等腰三角形.
為等腰三角形.
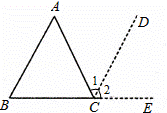
解:∠A+∠B+∠C=180°
理由:作∠ACD=∠A,并延長BC到E
∠1=∠A(已作)
∴AB∥CD ( )
∴∠B= ∠2 ( )
而∠ACB+∠1+∠2=180°
∴∠ACB+ ∠B + ∠A =180°( )
解:(1)如圖①AH=AB
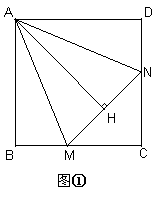 (2)數量關系成立.如圖②,延長CB至E,使BE=DN
(2)數量關系成立.如圖②,延長CB至E,使BE=DN
∵ABCD是正方形
∴AB=AD,∠D=∠ABE=90°
∴Rt△AEB≌Rt△AND
∴AE=AN,∠EAB=∠NAD
∴∠EAM=∠NAM=45°
∵AM=AM
∴△AEM≌△ANM
∵AB、AH是△AEM和△ANM對應邊上的高,
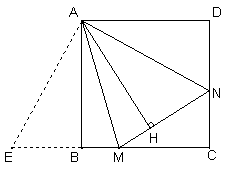 ∴AB=AH
∴AB=AH
(3)如圖③分別沿AM、AN翻折△AMH和△ANH,
得到△ABM和△AND
∴BM=2,DN=3,∠B=∠D=∠BAD=90°
分別延長BM和DN交于點C,得正方形ABCE.
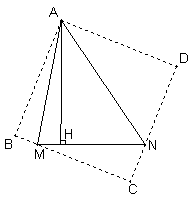 由(2)可知,AH=AB=BC=CD=AD.
由(2)可知,AH=AB=BC=CD=AD.
設AH=x,則MC=![]() , NC=
, NC=![]() 圖②
圖②
在Rt⊿MCN中,由勾股定理,得
![]()
∴![]()
解得![]() .(不符合題意,舍去)
.(不符合題意,舍去)
∴AH=6.
解:設這個正多邊形的邊數為n
由題意得:![]()
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com