題目列表(包括答案和解析)
函數
在區間
內的圖象是
函數
在區間
內的圖象是
函數
在區間
內的圖象是
（ ）
A. B. C. D.
函數
在區間
內的圖象是（ ）
函數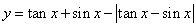
在區間
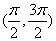內的圖象是
一、選擇題：本大題共12小題，每小題5分，共60分。
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
B
C
A
A
C
D
B
D
C
C
1．B.因
但
。
2．
.因
，
3．B. 因為
的定義域為[0，2]，所以對
，
但
故
。
4．
函數
為增函數
5．
，
，…，
6．
7. .由題知,垂足的軌跡為以焦距為直徑的圓,則
又
,所以
8. 
9. .
10．..函數
11..一天顯示的時間總共有
種,和為23總共有4種,故所求概率為
.
12．.當
時，顯然成立
當
時，顯然不成立；當
顯然成立；
當
時
，則
兩根為負，結論成立
故
二、填空題：本大題共4小題，每小題4分，共16分。
13.
14.. 
15.
5
16. A、B、D
13．依題意
14．
15. 易求得
、
到球心
的距離分別為3、2，類比平面內圓的情形可知當、與球心共線時，
取最大值5。
16.
, ∴對
取
的中點,則
, ∴
對
設
, 則
,而
,∴錯
又
,∴對
∴真命題的代號是
三、解答題：本大題共6小題，共74分。
17．解：（1）由
得
，
于是
=
.
（2）因為
所以
的最大值為
.
18．解：（1）令A表示兩年后柑桔產量恰好達到災前產量這一事件
（2）令B表示兩年后柑桔產量超過災前產量這一事件
19．（1）設
的公差為
，
的公比為
，則為正整數，
，
依題意有
①
解得
或
(舍去)
故
（2）
∴
20．解 ：（1）證明：依題設，
是
的中位線，所以∥
，
則∥平面
，所以∥
。
又
是的中點，所以
⊥，
則⊥。
因為
⊥
，⊥
，
所以⊥面，則⊥，
因此⊥面
。
（2）作
⊥
于，連
。
因為
⊥平面
，
根據三垂線定理知，⊥，
就是二面角
的平面角。
作
⊥
于，則∥，則是的中點，則
。
設
，由
得，
，解得
，
在
中，
，則，
。
所以
，故二面角為
。
解法二：（1）以直線
分別為
軸，建立空間直角坐標系，
則
所以
所以
所以
平面
由∥得∥，故：
平面
(2)由已知
設
則
由
與
共線得:存在
有
得
同理:
設
是平面
的一個法向量,
則
令
得
又
是平面的一個法量
所以二面角的大小為
21. 解：（1）因為
令
得
由
時，
在根的左右的符號如下表所示
極小值
極大值
極小值
所以的遞增區間為
的遞減區間為
（2）由（1）得到
，
要使的圖像與直線
恰有兩個交點，只要
或
，
即
或
.
22．（1）證明：設
，
則直線
的方程：
即：
因
在上，所以
①
又直線
方程：
由
得：
所以
同理，
所以直線的方程：
令
得
將①代入上式得
，即點在直線上
所以
三點共線
（2）解：由已知
共線，所以
以為直徑的圓的方程：
由
得
所以（舍去），
要使圓與拋物線有異于
的交點，則
所以存在
，使以為直徑的圓與拋物線有異于的交點
則
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com