
題目列表(包括答案和解析)
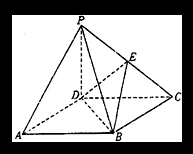
如圖,四棱錐![]() 的底面
的底面![]() 是正方形,側棱
是正方形,側棱![]() ⊥底面
⊥底面![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.
(1)證明:![]() //平面
//平面![]() ;
;
(2)在棱![]() 上是否存在點
上是否存在點![]() ,使三棱錐
,使三棱錐![]() 的
的
體積為![]() ?并說明理由.
?并說明理由.
|
(1)證明:![]() //平面
//平面![]() ;(2)在棱
;(2)在棱![]() 上是否存在點
上是否存在點![]() ,
,
使三棱錐![]() 的體積為
的體積為![]() ?并說明理由.
?并說明理由.
|
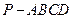 的底面
的底面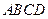 是正方形,側棱
是正方形,側棱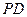 ⊥底面
⊥底面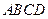 ,
,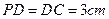 ,
,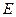 為
為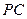 的中點. (1)證明:
的中點. (1)證明: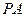 //平面
//平面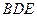 ;
;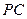 上是否存在點
上是否存在點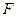 ,使三棱錐
,使三棱錐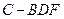 的
的 積為
積為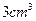 ?并說明理由.
?并說明理由.
|
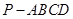 的底面
的底面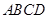 是正方形,側棱
是正方形,側棱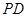 ⊥底面
⊥底面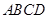 ,
,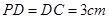 ,
, 為
為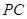 的中點.
的中點.
(1)證明: //平面
//平面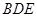 ;
;
(2)在棱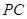 上是否存在點
上是否存在點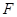 ,使三棱錐
,使三棱錐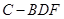 的
的
體積為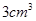 ?并說明理由.
?并說明理由.
如圖,四棱錐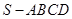 的底面是正方形,側棱
的底面是正方形,側棱 底面
底面 ,過
,過 作
作 垂直
垂直 交
交 于
于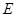 點,作
點,作 垂直
垂直 交
交 于
于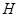 點,平面
點,平面 交
交 于
于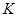 點,且
點,且 ,
, .
.
(1)試證明不論點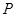 在何位置,都有
在何位置,都有 ;
;
(2)求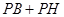 的最小值;
的最小值;
(3)設平面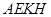 與平面
與平面 的交線為
的交線為 ,求證:
,求證: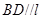 .
.
一、選擇題: C C D B D A A C B B A D

(2)由(Ⅰ) ,
, .
.
 的可能取值為:
的可能取值為: 、
、 、
、 、
、 .
.
則 ;
;
 ;
;
 ;
;
 .…………9分
.…………9分
∴ 的分布列為
的分布列為










 的數學期望
的數學期望 .…………12分
.…………12分
 故二面角
故二面角 的大小為
的大小為 …………………………12分
…………………………12分

解法二:如圖,以 為原點,建立空間直角坐標系,使
為原點,建立空間直角坐標系,使 軸,
軸, 、
、 分別在
分別在 軸、
軸、 軸上。
軸上。

20.解:(1)由題意知 即
即 ……2分
……2分
∴
 ……5分
……5分
檢驗知 、
、 時,結論也成立,故
時,結論也成立,故 .…………6分
.…………6分
(2)由于 ,故
,故

 .…………12分
.…………12分
21.解:(1)設 ,由
,由 知:R是TN的中點,…………………1分
知:R是TN的中點,…………………1分
則T(-x,0),R(0,
 ),
), =O 則(-x,-
=O 則(-x,-  )?(1,-
)?(1,-  )=0………………3分
)=0………………3分
∴ 點N的軌跡曲線C的方程為: ……………5分
……………5分
(2)設直線 的方程為
的方程為 ,代入曲線C的方程
,代入曲線C的方程 得:
得:  此方程有兩個不等實根,
此方程有兩個不等實根,
 ……………6分
……………6分
M在曲線C上,P、Q是直線 與曲線C的交點,
與曲線C的交點,
設 則
則 ,
,
 是以PQ為斜邊的直角三角形
是以PQ為斜邊的直角三角形 ……8分
……8分
 ,
, ,有
,有
由于 ,
,
∴ ∴
∴ …………10分
…………10分
t為點M的縱坐標, 關于
關于 的方程
的方程 有實根,
有實根,

 ,
,
直線 的斜率
的斜率 且
且 ,
, 或
或 …12分
…12分
22.解(1)
∴ 的增區間為
的增區間為 ,
, 減區間為
減區間為 和
和 .…………3分
.…………3分
極大值為 ,極小值為
,極小值為 .…………5分
.…………5分
(2)原不等式可化為 由(1)知,
由(1)知, 時,
時, 的最大值為
的最大值為 .
.
∴ 的最大值為
的最大值為 ,由恒成立的意義知道
,由恒成立的意義知道 ,從而
,從而 …8分
…8分
(3)設
則 .
.
∴當 時,
時, ,故
,故 在
在 上是減函數,
上是減函數,
又當 、
、 、
、 、
、 是正實數時,
是正實數時,
∴ .
.
由 的單調性有:
的單調性有: ,
,
即 .…………12′
.…………12′
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com