
題目列表(包括答案和解析)
已知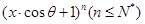 的展開式中,所有項的二項式系數(shù)之和為32,且展開式中含
的展開式中,所有項的二項式系數(shù)之和為32,且展開式中含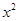 的系數(shù)與
的系數(shù)與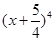 的展開式中
的展開式中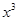 的系數(shù)相等,則銳角
的系數(shù)相等,則銳角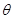 的值是
的值是
A. | B. | C. | D.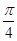 |
已知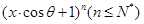 的展開式中,所有項的二項式系數(shù)之和為32,且展開式中含
的展開式中,所有項的二項式系數(shù)之和為32,且展開式中含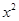 的系數(shù)與
的系數(shù)與 的展開式中
的展開式中 的系數(shù)相等,則銳角
的系數(shù)相等,則銳角 的值是
的值是
A. 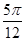 B.
B.
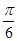 C.
C.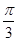 D.
D. 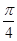
已知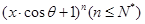 的展開式中,所有項的二項式系數(shù)之和為32,且展開式中含
的展開式中,所有項的二項式系數(shù)之和為32,且展開式中含 的系數(shù)與
的系數(shù)與 的展開式中
的展開式中 的系數(shù)相等,則銳角
的系數(shù)相等,則銳角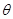 的值是( )
的值是( )
A.  B.
B.
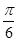 C.
C.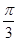 D.
D. 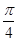
已知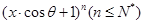 的展開式中,所有項的二項式系數(shù)之和為32,且展開式中含
的展開式中,所有項的二項式系數(shù)之和為32,且展開式中含 的系數(shù)與
的系數(shù)與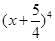 的展開式中
的展開式中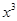 的系數(shù)相等,則銳角
的系數(shù)相等,則銳角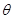 的值是
的值是
A.  B.
B.
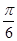 C.
C. D.
D. 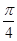
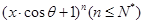 的展開式中,所有項的二項式系數(shù)之和為32,且展開式中含
的展開式中,所有項的二項式系數(shù)之和為32,且展開式中含 的系數(shù)與
的系數(shù)與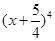 的展開式中
的展開式中 的系數(shù)相等,則銳角
的系數(shù)相等,則銳角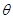 的值是
的值是A. | B. | C.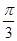 | D.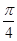 |
一、選擇題:
ACBDA CBADB CC
二、填空題:
13. 3 14. 10 15.學理).files/image184.gif) 16.
16. 學理).files/image186.gif)
三、解答題:
17.解; (I)
學理).files/image188.gif)
它的最小正周期學理).files/image190.gif)
(II)由(I)及學理).files/image129.gif) 得,
得,
學理).files/image193.gif)
學理).files/image195.gif)
由正弦定理,得學理).files/image197.gif)
18.解法一
(I)由已知。BC//AE,則AE與SB所成的角等于BC與SB所成的角。
連結SC. 由題設,學理).files/image199.gif) 為直二面角S-AE-C的平面角,于是EA、EC、ES兩兩互相垂直。
為直二面角S-AE-C的平面角,于是EA、EC、ES兩兩互相垂直。
在學理).files/image201.gif) 中,
中,學理).files/image203.gif) 則
則學理).files/image205.gif)
在學理).files/image207.gif) 中,
中, 學理).files/image209.gif) 則
則學理).files/image211.gif)
易見,學理).files/image213.gif) 平面
平面學理).files/image215.gif) , 則
, 則學理).files/image217.gif) 平面
平面學理).files/image215.gif) ,從而
,從而學理).files/image220.gif)
在學理).files/image222.gif) 中,
中,學理).files/image224.gif)
所以AE與SB所成角的大小為學理).files/image226.gif)
(II)學理).files/image228.gif) 平面
平面學理).files/image230.gif) ,
,學理).files/image232.gif) 平面
平面學理).files/image234.gif) 平面
平面學理).files/image230.gif)
作學理).files/image236.gif) 于O,則
于O,則學理).files/image238.gif) 平面
平面學理).files/image240.gif) ,作
,作學理).files/image242.gif) 于F,連結AF, 則
于F,連結AF, 則學理).files/image244.gif)
學理).files/image246.gif) 為二面角A-SB-E的平面角
為二面角A-SB-E的平面角
在學理).files/image248.gif) 中,
中,學理).files/image250.gif)
因為學理).files/image252.gif) ,所以
,所以學理).files/image254.gif) ,則
,則學理).files/image256.gif)
學理).files/image258.gif)
故二面角A-SB-E的大小為學理).files/image260.gif)
學理).files/image262.jpg)
解法二:
(I)有題設,為直二面角S-AE-C的平面角,于是EA、EC、ES兩兩互相垂直,
建立如圖所示的空間直角坐標系學理).files/image264.gif) ,其中,
,其中,
學理).files/image266.gif)
學理).files/image268.gif)
學理).files/image270.gif)
所以,AE與SB所成角的大小為學理).files/image272.gif)
(II)設學理).files/image274.gif) 為,面SBE的法向量,則
為,面SBE的法向量,則學理).files/image276.gif) ,且
,且學理).files/image278.gif)
學理).files/image280.gif)
設學理).files/image282.gif) 為面SAB的法向量,則
為面SAB的法向量,則學理).files/image284.gif) ,且
,且學理).files/image286.gif)
學理).files/image288.gif)
以內二面角A-SB-E為銳角,所以其大小為學理).files/image290.gif)
19.解:
學理).files/image137.gif) 的可能值為,1,2,3,其中
的可能值為,1,2,3,其中
學理).files/image293.gif)
學理).files/image137.gif) 的分布列為
的分布列為
學理).files/image137.gif)
1
2
3
P
學理).files/image297.gif)
學理).files/image299.gif)
學理).files/image301.gif)
學理).files/image137.gif) 的期望
的期望學理).files/image303.gif)
20.解:
(I)學理).files/image305.gif)
依題意,曲線學理).files/image141.gif) 與直線
與直線學理).files/image145.gif) 相切于
相切于學理).files/image309.gif) ,所以
,所以
學理).files/image311.gif)
(II)
(1)當學理).files/image313.gif) 時,
時,學理).files/image315.gif) ,
,學理).files/image123.gif) 在
在學理).files/image318.gif) 上單調遞增,在
上單調遞增,在學理).files/image143.gif) 處取得最大值
處取得最大值
(2)當學理).files/image321.gif) 時,
時,學理).files/image315.gif) ,
,學理).files/image123.gif) 在
在學理).files/image318.gif) 上單調遞減,不在
上單調遞減,不在學理).files/image143.gif) 處取得最大值
處取得最大值
(3)當學理).files/image324.gif) 時。由
時。由學理).files/image315.gif) ,得
,得學理).files/image326.gif) ;由
;由學理).files/image328.gif) ,得
,得學理).files/image330.gif)
所以學理).files/image123.gif) 在
在學理).files/image332.gif) 單調遞減,在
單調遞減,在學理).files/image334.gif) 單調遞增
單調遞增
此時,學理).files/image123.gif) 在
在學理).files/image143.gif) 或
或學理).files/image336.gif) 處取得最大值,所以當且僅當
處取得最大值,所以當且僅當學理).files/image338.gif) ,
,學理).files/image340.gif) 時,
時,學理).files/image123.gif) 在
在學理).files/image143.gif) 處取得最大值,此時解得
處取得最大值,此時解得學理).files/image342.gif) ,
,
綜上,學理).files/image093.gif) 的取值范圍是
的取值范圍是學理).files/image345.gif)
21.解:
(I)由學理).files/image153.gif) ,得
,得學理).files/image348.gif) ,代入
,代入學理).files/image350.gif) ,得
,得學理).files/image352.gif)
設學理).files/image354.gif) ,則
,則學理).files/image356.gif) 是這個一元二次方程的兩個根,
是這個一元二次方程的兩個根,
學理).files/image358.gif) ①
①
由學理).files/image360.gif) ,及
,及學理).files/image362.gif) ,得
,得學理).files/image364.gif)
由根與系數(shù)的關系,得
學理).files/image366.gif) ②
②
學理).files/image368.gif) ③
③
由②式得學理).files/image370.gif) ,代入③式,得
,代入③式,得學理).files/image372.gif)
學理).files/image374.gif) ④
④
由學理).files/image376.gif) ,及①、④,得
,及①、④,得學理).files/image378.gif)
解不等式組,得學理).files/image380.gif)
所以學理).files/image093.gif) 的取值范圍是
的取值范圍是學理).files/image383.gif)
(II)
學理).files/image385.gif)
22.解:(I)
(Ⅰ)0<an+1<f(an)即0<an+1<,∴>+2,+1>3(+1),
當n≥2時,+1>3(+1)>32(+1)>…>3n-1(+1)=3n≥32=9,
∴an<
(Ⅱ)bn=g(an)=
S1=<,
當n≥2時,由(Ⅰ)的證明,知<,
Sn<+++…+==(1-)<.
綜上,總有Sn<(n∈N*)
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com