
題目列表(包括答案和解析)
已知向量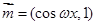 ,
,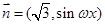 (
(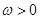 ),函數(shù)
),函數(shù)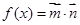 ,且
,且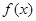 圖象上一個最高點為
圖象上一個最高點為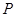
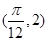 ,與
,與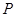 最近的一個最低點的坐標(biāo)為
最近的一個最低點的坐標(biāo)為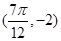 .
.
(1)求函數(shù)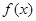 的解析式;
的解析式;
(2)設(shè) 為常數(shù),判斷方程
為常數(shù),判斷方程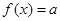 在區(qū)間
在區(qū)間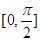 上的解的個數(shù);
上的解的個數(shù);
(3)在銳角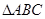 中,若
中,若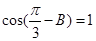 ,求
,求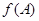 的取值范圍.
的取值范圍.
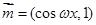 ,
,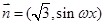 (
(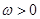 ),函數(shù)
),函數(shù)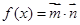 ,且
,且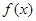 圖象上一個最高點為
圖象上一個最高點為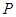
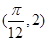 ,與
,與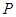 最近的一個最低點的坐標(biāo)為
最近的一個最低點的坐標(biāo)為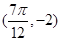 .
.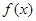 的解析式;
的解析式;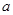 為常數(shù),判斷方程
為常數(shù),判斷方程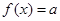 在區(qū)間
在區(qū)間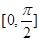 上的解的個數(shù);
上的解的個數(shù);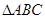 中,若
中,若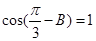 ,求
,求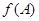 的取值范圍.
的取值范圍. ,
,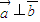 .且
.且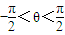 . 求θ;
. 求θ;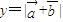 的單調(diào)增區(qū)間和函數(shù)圖象的對稱軸方程.
的單調(diào)增區(qū)間和函數(shù)圖象的對稱軸方程. =
=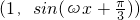 ,
, =
=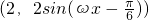 (其中ω為正常數(shù))
(其中ω為正常數(shù))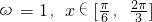 ,求
,求 ∥
∥ 時tanx的值;
時tanx的值; •
• -2,若函數(shù)f(x)的圖象的相鄰兩個對稱中心的距離為
-2,若函數(shù)f(x)的圖象的相鄰兩個對稱中心的距離為 ,求f(x)在區(qū)間
,求f(x)在區(qū)間 上的最小值.
上的最小值. =
= ,
, =
= (其中ω為正常數(shù))
(其中ω為正常數(shù)) ,求
,求 ∥
∥ 時tanx的值;
時tanx的值;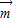 •
• -2,若函數(shù)f(x)的圖象的相鄰兩個對稱中心的距離為
-2,若函數(shù)f(x)的圖象的相鄰兩個對稱中心的距離為 ,求f(x)在區(qū)間
,求f(x)在區(qū)間 上的最小值.
上的最小值.一、選擇題: C C D B D A A C B B A D
研試題----理科數(shù)學(xué).files/image282.jpg)
(2)由(Ⅰ)研試題----理科數(shù)學(xué).files/image284.gif) ,
,研試題----理科數(shù)學(xué).files/image286.gif) .
.
研試題----理科數(shù)學(xué).files/image210.gif) 的可能取值為:
的可能取值為:研試題----理科數(shù)學(xué).files/image289.gif) 、
、研試題----理科數(shù)學(xué).files/image159.gif) 、
、研試題----理科數(shù)學(xué).files/image292.gif) 、
、研試題----理科數(shù)學(xué).files/image294.gif) .
.
則研試題----理科數(shù)學(xué).files/image296.gif) ;
;
研試題----理科數(shù)學(xué).files/image298.gif) ;
;
研試題----理科數(shù)學(xué).files/image300.gif) ;
;
研試題----理科數(shù)學(xué).files/image302.gif) .…………9分
.…………9分
∴研試題----理科數(shù)學(xué).files/image210.gif) 的分布列為
的分布列為
研試題----理科數(shù)學(xué).files/image210.gif)
研試題----理科數(shù)學(xué).files/image289.gif)
研試題----理科數(shù)學(xué).files/image159.gif)
研試題----理科數(shù)學(xué).files/image292.gif)
研試題----理科數(shù)學(xué).files/image294.gif)
研試題----理科數(shù)學(xué).files/image050.gif)
研試題----理科數(shù)學(xué).files/image309.gif)
研試題----理科數(shù)學(xué).files/image311.gif)
研試題----理科數(shù)學(xué).files/image313.gif)
研試題----理科數(shù)學(xué).files/image315.gif)
研試題----理科數(shù)學(xué).files/image317.gif) 的數(shù)學(xué)期望
的數(shù)學(xué)期望研試題----理科數(shù)學(xué).files/image319.gif) .…………12分
.…………12分
研試題----理科數(shù)學(xué).files/image321.jpg) 故二面角
故二面角研試題----理科數(shù)學(xué).files/image323.gif) 的大小為
的大小為研試題----理科數(shù)學(xué).files/image325.gif) …………………………12分
…………………………12分
研試題----理科數(shù)學(xué).files/image327.jpg)
解法二:如圖,以研試題----理科數(shù)學(xué).files/image226.gif) 為原點,建立空間直角坐標(biāo)系,使
為原點,建立空間直角坐標(biāo)系,使研試題----理科數(shù)學(xué).files/image330.gif) 軸,
軸,研試題----理科數(shù)學(xué).files/image332.gif) 、
、研試題----理科數(shù)學(xué).files/image334.gif) 分別在
分別在研試題----理科數(shù)學(xué).files/image336.gif) 軸、
軸、研試題----理科數(shù)學(xué).files/image338.gif) 軸上。
軸上。
研試題----理科數(shù)學(xué).files/image339.gif)
20.解:(1)由題意知研試題----理科數(shù)學(xué).files/image341.gif) 即
即研試題----理科數(shù)學(xué).files/image343.gif) ……2分
……2分
∴研試題----理科數(shù)學(xué).files/image345.gif)
研試題----理科數(shù)學(xué).files/image347.gif) ……5分
……5分
檢驗知研試題----理科數(shù)學(xué).files/image349.gif) 、
、研試題----理科數(shù)學(xué).files/image292.gif) 時,結(jié)論也成立,故
時,結(jié)論也成立,故研試題----理科數(shù)學(xué).files/image352.gif) .…………6分
.…………6分
(2)由于研試題----理科數(shù)學(xué).files/image354.gif) ,故
,故
研試題----理科數(shù)學(xué).files/image356.gif)
研試題----理科數(shù)學(xué).files/image358.gif) .…………12分
.…………12分
21.解:(1)設(shè)研試題----理科數(shù)學(xué).files/image360.gif) ,由
,由研試題----理科數(shù)學(xué).files/image362.gif) 知:R是TN的中點,…………………1分
知:R是TN的中點,…………………1分
則T(-x,0),R(0,
研試題----理科數(shù)學(xué).files/image364.gif) ),
),研試題----理科數(shù)學(xué).files/image366.gif) =O 則(-x,-
=O 則(-x,- 研試題----理科數(shù)學(xué).files/image364.gif) )?(1,-
)?(1,- 研試題----理科數(shù)學(xué).files/image364.gif) )=0………………3分
)=0………………3分
∴ 點N的軌跡曲線C的方程為:研試題----理科數(shù)學(xué).files/image369.gif) ……………5分
……………5分
(2)設(shè)直線研試題----理科數(shù)學(xué).files/image371.gif) 的方程為
的方程為研試題----理科數(shù)學(xué).files/image373.gif) ,代入曲線C的方程
,代入曲線C的方程研試題----理科數(shù)學(xué).files/image369.gif) 得:
得: 研試題----理科數(shù)學(xué).files/image376.gif) 此方程有兩個不等實根,
此方程有兩個不等實根,
研試題----理科數(shù)學(xué).files/image378.gif) ……………6分
……………6分
M在曲線C上,P、Q是直線研試題----理科數(shù)學(xué).files/image371.gif) 與曲線C的交點,
與曲線C的交點,
設(shè)研試題----理科數(shù)學(xué).files/image381.gif) 則
則研試題----理科數(shù)學(xué).files/image383.gif) ,
,
研試題----理科數(shù)學(xué).files/image385.gif) 是以PQ為斜邊的直角三角形
是以PQ為斜邊的直角三角形研試題----理科數(shù)學(xué).files/image387.gif) ……8分
……8分
研試題----理科數(shù)學(xué).files/image389.gif) ,
,研試題----理科數(shù)學(xué).files/image391.gif) ,有
,有研試題----理科數(shù)學(xué).files/image393.gif)
由于研試題----理科數(shù)學(xué).files/image395.gif) ,
,
∴研試題----理科數(shù)學(xué).files/image397.gif) ∴
∴研試題----理科數(shù)學(xué).files/image399.gif) …………10分
…………10分
t為點M的縱坐標(biāo),研試題----理科數(shù)學(xué).files/image401.gif) 關(guān)于
關(guān)于研試題----理科數(shù)學(xué).files/image403.gif) 的方程
的方程研試題----理科數(shù)學(xué).files/image405.gif) 有實根,
有實根,
研試題----理科數(shù)學(xué).files/image407.gif)
研試題----理科數(shù)學(xué).files/image409.gif) ,
,
直線研試題----理科數(shù)學(xué).files/image371.gif) 的斜率
的斜率研試題----理科數(shù)學(xué).files/image412.gif) 且
且研試題----理科數(shù)學(xué).files/image414.gif) ,
,研試題----理科數(shù)學(xué).files/image416.gif) 或
或研試題----理科數(shù)學(xué).files/image418.gif) …12分
…12分
22.解(1)研試題----理科數(shù)學(xué).files/image420.gif)
∴研試題----理科數(shù)學(xué).files/image200.gif) 的增區(qū)間為
的增區(qū)間為研試題----理科數(shù)學(xué).files/image422.gif) ,
,研試題----理科數(shù)學(xué).files/image200.gif) 減區(qū)間為
減區(qū)間為研試題----理科數(shù)學(xué).files/image424.gif) 和
和研試題----理科數(shù)學(xué).files/image426.gif) .…………3分
.…………3分
極大值為研試題----理科數(shù)學(xué).files/image428.gif) ,極小值為
,極小值為研試題----理科數(shù)學(xué).files/image430.gif) .…………5分
.…………5分
(2)原不等式可化為研試題----理科數(shù)學(xué).files/image432.gif) 由(1)知,
由(1)知,研試題----理科數(shù)學(xué).files/image266.gif) 時,
時,研試題----理科數(shù)學(xué).files/image435.gif) 的最大值為
的最大值為研試題----理科數(shù)學(xué).files/image437.gif) .
.
∴研試題----理科數(shù)學(xué).files/image439.gif) 的最大值為
的最大值為研試題----理科數(shù)學(xué).files/image441.gif) ,由恒成立的意義知道
,由恒成立的意義知道研試題----理科數(shù)學(xué).files/image443.gif) ,從而
,從而研試題----理科數(shù)學(xué).files/image445.gif) …8分
…8分
(3)設(shè)研試題----理科數(shù)學(xué).files/image447.gif)
則研試題----理科數(shù)學(xué).files/image449.gif) .
.
∴當(dāng)研試題----理科數(shù)學(xué).files/image451.gif) 時,
時,研試題----理科數(shù)學(xué).files/image453.gif) ,故
,故研試題----理科數(shù)學(xué).files/image455.gif) 在
在研試題----理科數(shù)學(xué).files/image457.gif) 上是減函數(shù),
上是減函數(shù),
又當(dāng)研試題----理科數(shù)學(xué).files/image271.gif) 、
、研試題----理科數(shù)學(xué).files/image273.gif) 、
、研試題----理科數(shù)學(xué).files/image036.gif) 、
、研試題----理科數(shù)學(xué).files/image276.gif) 是正實數(shù)時,
是正實數(shù)時,研試題----理科數(shù)學(xué).files/image459.gif)
∴研試題----理科數(shù)學(xué).files/image461.gif) .
.
由研試題----理科數(shù)學(xué).files/image455.gif) 的單調(diào)性有:
的單調(diào)性有:研試題----理科數(shù)學(xué).files/image463.gif) ,
,
即研試題----理科數(shù)學(xué).files/image465.gif) .…………12′
.…………12′
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com