
題目列表(包括答案和解析)
已知正項數列 的前n項和
的前n項和 滿足:
滿足: ,
,
(1)求數列 的通項
的通項 和前n項和
和前n項和 ;
;
(2)求數列 的前n項和
的前n項和 ;
;
(3)證明:不等式  對任意的
對任意的 ,
, 都成立.
都成立.
【解析】第一問中,由于 所以
所以
兩式作差 ,然后得到
,然后得到
從而 得到結論
得到結論
第二問中, 利用裂項求和的思想得到結論。
利用裂項求和的思想得到結論。
第三問中,

又
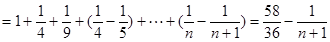
結合放縮法得到。
解:(1)∵ ∴
∴
∴
∴ ∴
∴  ………2分
………2分
又∵正項數列 ,∴
,∴ ∴
∴
又n=1時,
∴ ∴數列
∴數列 是以1為首項,2為公差的等差數列……………3分
是以1為首項,2為公差的等差數列……………3分
∴ …………………4分
…………………4分
∴ …………………5分
…………………5分
(2) …………………6分
…………………6分
∴
 …………………9分
…………………9分
(3)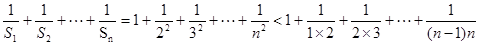
 …………………12分
…………………12分
又

 ,
,
∴不等式  對任意的
對任意的 ,
, 都成立.
都成立.
我們已學過的算法有求解一元二次方程的求根公式,加減消元法求二元一次方程組解,二分法求函數零點等.對算法的描述有
①對一類問題都有效;
②對個別問題有效;
③計算可以一步步地進行,每一步都有惟一的結果;
④是一種通法,只要按部就班地做,總能得到結果.
以上正確描述算法的有
| n |
 |
| k=1 |
| 1 |
| lg(ak+2)lg(ak+1+2) |
| lim |
| n→∞ |
| 1 | 2 |
以上描述算法的說法中,正確的有( )
A.1個 B.2個 C.3個 D.4個
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com