
題目列表(包括答案和解析)
 =1(a>b>0)的離心率為e=
=1(a>b>0)的離心率為e= ,直線l被圓O截得的弦長與橢圓的長軸長相等.
,直線l被圓O截得的弦長與橢圓的長軸長相等.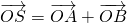 (O是坐標原點),是否存在這樣的直線l,使四邊形為ASB的對角線長相等?若存在,求出直線l的方程,若不存在,說明理由.
(O是坐標原點),是否存在這樣的直線l,使四邊形為ASB的對角線長相等?若存在,求出直線l的方程,若不存在,說明理由.已知直線![]() ,圓O:
,圓O:![]() =36(O為坐標原點),橢圓C:
=36(O為坐標原點),橢圓C:![]() =1(a>b>0)的離心率為e=
=1(a>b>0)的離心率為e=![]() ,直線l被圓O截得的弦長與橢圓的長軸長相等。
,直線l被圓O截得的弦長與橢圓的長軸長相等。
(I)求橢圓C的方程;(II)過點(3,0)作直線l,與橢圓C交于A,B兩點設![]() (O是坐標原點),是否存在這樣的直線l,使四邊形為ASB的對角線長相等?若存在 ,求出直線l的方程,若不存在,說明理由。
(O是坐標原點),是否存在這樣的直線l,使四邊形為ASB的對角線長相等?若存在 ,求出直線l的方程,若不存在,說明理由。
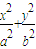 =1(a>b>0)的離心率為e=
=1(a>b>0)的離心率為e=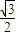 ,直線l被圓O截得的弦長與橢圓的長軸長相等.
,直線l被圓O截得的弦長與橢圓的長軸長相等.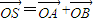 (O是坐標原點),是否存在這樣的直線l,使四邊形為ASB的對角線長相等?若存在,求出直線l的方程,若不存在,說明理由.
(O是坐標原點),是否存在這樣的直線l,使四邊形為ASB的對角線長相等?若存在,求出直線l的方程,若不存在,說明理由.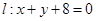 ,圓O:
,圓O: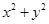 =36(O為坐標原點),橢圓C:
=36(O為坐標原點),橢圓C: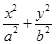 =1(a>b>0)的離心率為e=
=1(a>b>0)的離心率為e=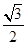 ,直線l被圓O截得的弦長與橢圓的長軸長相等。
,直線l被圓O截得的弦長與橢圓的長軸長相等。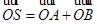 (O是坐標原點),是否存在這樣的直線l,使四邊形為ASB的對角線長相等?若存在 ,求出直線l的方程,若不存在,說明理由。
(O是坐標原點),是否存在這樣的直線l,使四邊形為ASB的對角線長相等?若存在 ,求出直線l的方程,若不存在,說明理由。| x2 |
| a2 |
| y2 |
| b2 |
| CP |
| PD |
| CQ |
| QD |
一、選擇題
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
B
A
C
A
B
D
B
D
C
A
C
二、填空題
13.30° 14..files/image163.gif) 15.-0.61 16.
15.-0.61 16..files/image165.gif)
三、解答題
17.解:(I).files/image110.gif)
即.files/image168.gif) 中出現3個1,2個0
2分
中出現3個1,2個0
2分
所以.files/image170.gif) 6分
6分
(II)(法一)設Y=X-1,
由題知.files/image172.gif) 9分
9分
所以.files/image174.gif) 12分
12分
(法二)X的分布列如下:
X
1
2
3
4
P(X)
.files/image176.gif)
.files/image178.gif)
.files/image180.gif)
.files/image182.gif)
X
5
6
P(X)
.files/image184.gif)
.files/image186.gif)
……10服
所以.files/image188.gif) …………12分
…………12分
18.解:(I)由三視圖可得,三棱錐A―BCD中
.files/image190.gif) 都等于90°,
都等于90°,
每個面都是直角三角形;
可得.files/image192.gif) 面ADB,所以
面ADB,所以.files/image194.gif) ……2分
……2分
又.files/image196.gif) ,所以
,所以.files/image198.gif) 面ABC,
面ABC,
所以DE.files/image200.gif) AC, 4分
AC, 4分
又DF.files/image200.gif) AC,所以AC
AC,所以AC.files/image200.gif) 面DEF。
6分
面DEF。
6分
(II)方法一:由(I)知.files/image202.gif) 為二面角B―AC―D的平面角, 9分
為二面角B―AC―D的平面角, 9分