
題目列表(包括答案和解析)
如圖所示,將一矩形花壇ABCD擴建成一個更大的矩形花壇AMPN,要求B在AM上,D在AN上,且對角線MN過C點,已知|AB|=3米,|AD|=2米,
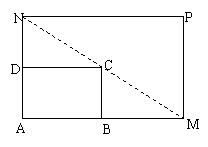 (1) 要使矩形AMPN的面積大于32平方米,則AN的長應在什么范圍內?
(1) 要使矩形AMPN的面積大于32平方米,則AN的長應在什么范圍內?
(2) 若|AN| ![]() (單位:米),則當AM、AN的長度是多少時,矩形花壇AMPN的面積最大?并求出最大面積.
(單位:米),則當AM、AN的長度是多少時,矩形花壇AMPN的面積最大?并求出最大面積.
 如圖所示,將一矩形花壇ABCD擴建成一個更大的矩形花壇AMPN,要求B在AM上,D在AN上,對角線MN過C點,已知|AB|=3米,|AD|=2米,且受地理條件限制,|AN|長不超過8米,設AN=x.
如圖所示,將一矩形花壇ABCD擴建成一個更大的矩形花壇AMPN,要求B在AM上,D在AN上,對角線MN過C點,已知|AB|=3米,|AD|=2米,且受地理條件限制,|AN|長不超過8米,設AN=x.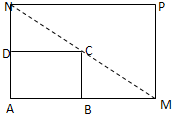 如圖所示,將一矩形花壇ABCD擴建成一個更大的矩形花壇AMPN,要求B在AM上,D在AN上,對角線MN過C點,已知|AB|=3米,|AD|=2米,且受地理條件限制,|AN|長不超過8米,設AN=x.
如圖所示,將一矩形花壇ABCD擴建成一個更大的矩形花壇AMPN,要求B在AM上,D在AN上,對角線MN過C點,已知|AB|=3米,|AD|=2米,且受地理條件限制,|AN|長不超過8米,設AN=x.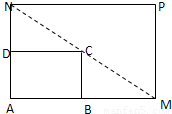

一、本解答給出了一種或幾種解法供參考,如果考生的解法與本解答不同,可根據試題的主要考查內容比照評分標準制訂相應的評分細則.
二、對計算題當考生的解答在某一步出現錯誤時,如果后續部分的解答未改變該題的內容和難度,可視影響的程度決定給分,但不得超過該部分正確解答應得分數的一半;如果后續部分的解答有較嚴重的錯誤,就不再給分.
三、解答右端所注分數,表示考生正確做到這一步應得的累加分數.
四、只給整數分數,選擇題和填空題不給中間分數.
一.選擇題:CCDAB CBDAD
1..files/image250.gif) 則
則.files/image252.gif) 選C.
選C.
2.將各選項代入檢驗易得答案選C.
3.由函數以.files/image040.gif) 為周期,可排除A、B,由函數在
為周期,可排除A、B,由函數在.files/image038.gif) 為增函數,可排除C,故選D。
為增函數,可排除C,故選D。
5.正確命題有②、④,故選B.
6..files/image254.gif) 或
或.files/image256.gif)
.files/image258.gif) 或
或.files/image085.gif) ,故選C。
,故選C。
7.將圓的方程化為標準方程得.files/image261.gif) ,由數形結合不難得出所求的距離差為已知圓的直徑長
,由數形結合不難得出所求的距離差為已知圓的直徑長.files/image098.gif) .,故選B.
.,故選B.
8.該程序的功能是求和.files/image263.gif) ,因輸出結果
,因輸出結果.files/image265.gif) ,故選D.
,故選D.
.files/image267.gif)
.files/image269.gif) 9.如圖設點P為AB的三等分點,要使△PBC的面積不小于
9.如圖設點P為AB的三等分點,要使△PBC的面積不小于.files/image114.gif) ,則點P只能在
,則點P只能在
AP上選取,由幾何概型的概率
公式得所求概率為.files/image271.gif) .故選A.
.故選A.
10.如圖:易得答案選D.
二.填空題:11.800、20%;12. 3;13. ①③④⑤;14. .files/image098.gif) ; 15.
; 15. .files/image274.gif)
11.由率分布直方圖知,及格率=.files/image276.gif) =80%,
=80%,
及格人數=80%×1000=800,優秀率=.files/image278.gif) %.
%.
.files/image280.gif) 12.由
12.由.files/image137.gif) 得
得.files/image282.gif)
由.files/image284.gif) ,得
,得.files/image286.gif)
13.顯然①可能,②不可能,③④⑤如右圖知都有可能。
14.在平面直角坐標系中,曲線.files/image149.gif) 和
和.files/image151.gif) 分別表示圓
分別表示圓.files/image288.gif) 和直線
和直線.files/image290.gif) ,易知
,易知.files/image155.gif) =
=.files/image098.gif)
15. C為圓周上一點,AB是直徑,所以AC⊥BC,而BC=3,AB=6,得∠BAC=30°,進而得∠B=60°,所以∠DCA=60°,又∠ADC=90°,得∠DAC=30°,
.files/image293.gif)
三.解答題:
16.解:(1).files/image295.gif)
.files/image297.gif)
.files/image299.gif) ------------------------4分
------------------------4分
(2)∵.files/image162.gif) ,
,.files/image164.gif)
.files/image301.gif) ∴
∴.files/image303.gif) ,
,
由正弦定理得:.files/image305.gif)
∴.files/image307.gif) ------------6分
------------6分
如圖過點B作.files/image309.gif) 垂直于對岸,垂足為D,則BD的長就是該河段的寬度。
垂直于對岸,垂足為D,則BD的長就是該河段的寬度。
在.files/image311.gif) 中,∵
中,∵.files/image313.gif) ,
,.files/image315.gif) ------------8分
------------8分
∴.files/image317.gif) =
=.files/image319.gif)
.files/image321.gif) (米)
(米)
∴該河段的寬度.files/image323.gif) 米。---------------------------12分
米。---------------------------12分
17.解:(1)設.files/image325.gif)
.files/image327.gif) ,(
,(.files/image329.gif) )由
)由.files/image172.gif)
.files/image174.gif) 成等比數列得
成等比數列得
.files/image331.gif) ,----------------①,
,----------------①, .files/image333.gif) 得
得.files/image335.gif)
.files/image337.gif)
∵.files/image329.gif) ∴
∴.files/image339.gif) ---------------②
---------------②
由①②得.files/image341.gif) , ∴
, ∴.files/image343.gif) -----------------------------4分
-----------------------------4分
∴.files/image345.gif) ,顯然數列
,顯然數列.files/image347.gif) 是首項
是首項.files/image349.gif) 公差
公差.files/image351.gif) 的等差數列
的等差數列
∴.files/image180.gif) =
=.files/image353.gif) ------------------------------------6分
------------------------------------6分
[或.files/image355.gif) ]
]
(2)∵.files/image357.gif)
∴.files/image359.gif) =
=.files/image361.gif) ------------8分
------------8分
2.files/image186.gif) =
=.files/image363.gif)
-.files/image186.gif) =
=.files/image365.gif) =
=.files/image367.gif) ---10分
---10分
∴.files/image186.gif) =
=.files/image369.gif) 。------------------------------------------12分
。------------------------------------------12分
18.(1)解:∵.files/image192.gif)
∴.files/image371.gif) 且
且.files/image373.gif) ,
,
∴.files/image375.gif) 平面
平面.files/image377.gif) ------------ ----------------2分
------------ ----------------2分
.files/image188.gif) 在
在.files/image379.gif) 中,
中, .files/image381.gif) ,
,
.files/image383.gif) 中,
中,.files/image385.gif)
∵.files/image387.gif) ,
,
∴.files/image389.gif) .--------------4分
.--------------4分
(2)證法1:由(1)知SA=2, 在.files/image391.gif) 中,
中,.files/image393.gif) ---6分
---6分
∵.files/image395.gif) ,∴
,∴.files/image196.gif) -------------------8分
-------------------8分
〔證法2:由(1)知.files/image375.gif) 平面
平面.files/image377.gif) ,∵
,∵.files/image397.gif) 面
面.files/image377.gif) ,
,
∴.files/image400.gif) ,∵
,∵.files/image402.gif) ,
,.files/image404.gif) ,∴
,∴.files/image406.gif) 面
面.files/image408.gif)
又∵.files/image410.gif) 面
面.files/image408.gif) ,∴
,∴.files/image196.gif) 〕
〕
(3) ∵.files/image371.gif)
∴.files/image413.gif) 為二面角C-SA-B的平面角---------10分
為二面角C-SA-B的平面角---------10分
在.files/image415.gif) 中,∵
中,∵.files/image417.gif)
∴.files/image419.gif) ,
,
∴即所求二面角C-SA-B為.files/image421.gif) -------------------------14分
-------------------------14分
.files/image423.gif) 19.解:(1)依題意知,動點
19.解:(1)依題意知,動點.files/image206.gif) 到定點
到定點.files/image200.gif)
.files/image202.gif) 的距離等于
的距離等于.files/image206.gif) 到直線
到直線.files/image426.gif) 的距離,曲線
的距離,曲線.files/image208.gif) 是以原點為頂點,
是以原點為頂點,.files/image200.gif)
.files/image202.gif) 為焦點的拋物線………………………………2分
為焦點的拋物線………………………………2分
∵.files/image429.gif) ∴
∴.files/image431.gif)
∴ 曲線.files/image208.gif) 方程是
方程是.files/image434.gif) ………4分
………4分
(2)設圓的圓心為.files/image436.gif) ,∵圓
,∵圓.files/image210.gif) 過
過.files/image008.gif)
.files/image213.gif) ,
,
∴圓的方程為 .files/image439.gif) ……………………………7分
……………………………7分
令.files/image441.gif) 得:
得:.files/image443.gif)
設圓與.files/image204.gif) 軸的兩交點分別為
軸的兩交點分別為.files/image446.gif) ,
,.files/image448.gif)
方法1:不妨設.files/image450.gif)
.files/image452.gif) ,由求根公式得
,由求根公式得
.files/image454.gif) ,
,.files/image456.gif) …………………………10分
…………………………10分
∴.files/image458.gif)
又∵點.files/image436.gif) 在拋物線
在拋物線.files/image434.gif) 上,∴
上,∴.files/image460.gif) ,
,
∴ .files/image462.gif) ,即
,即.files/image218.gif) =4--------------------------------------------------------13分
=4--------------------------------------------------------13分
∴當.files/image210.gif) 運動時,弦長
運動時,弦長.files/image218.gif) 為定值4…………………………………………………14分
為定值4…………………………………………………14分
〔方法2:∵.files/image464.gif) ,
,.files/image466.gif)
∴.files/image452.gif)
.files/image468.gif)
.files/image470.gif)
又∵點.files/image436.gif) 在拋物線
在拋物線.files/image434.gif) 上,∴
上,∴.files/image460.gif) , ∴
, ∴ .files/image472.gif)
.files/image474.gif)
∴當.files/image210.gif) 運動時,弦長
運動時,弦長.files/image218.gif) 為定值4〕
為定值4〕
20. 解:設AN的長為x米(x >2)
∵.files/image476.gif) ,∴|AM|=
,∴|AM|=.files/image478.gif)
∴SAMPN=|AN|•|AM|=.files/image480.gif) ------------------------------------- 4分
------------------------------------- 4分
(1)由SAMPN > 32 得 .files/image480.gif) > 32 ,
> 32 ,
∵x >2,∴.files/image482.gif) ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0
∴.files/image484.gif) 即AN長的取值范圍是
即AN長的取值范圍是.files/image486.gif) ----------- 8分
----------- 8分
(2)令y=.files/image480.gif) ,則y′=
,則y′=.files/image488.gif) -------------- 10分
-------------- 10分
∵當.files/image490.gif) ,y′< 0,∴函數y=
,y′< 0,∴函數y=.files/image480.gif) 在
在.files/image492.gif) 上為單調遞減函數,
上為單調遞減函數,
∴當x=3時y=.files/image480.gif) 取得最大值,即
取得最大值,即.files/image494.gif) (平方米)
(平方米)
此時|AN|=3米,|AM|=.files/image496.gif) 米 ----------------------
12分
米 ----------------------
12分
21.解:
(1).files/image498.gif)
.files/image500.gif)
.files/image502.gif) ---------------2分
---------------2分
當.files/image504.gif) 時
時.files/image506.gif) ,函數
,函數.files/image227.gif) 有一個零點;--------------3分
有一個零點;--------------3分
當.files/image508.gif) 時,
時,.files/image510.gif) ,函數
,函數.files/image227.gif) 有兩個零點。------------4分
有兩個零點。------------4分
(2)令.files/image512.gif) ,則
,則
.files/image514.gif)
.files/image516.gif) ,
,
.files/image518.gif)
.files/image520.gif) 在
在.files/image237.gif) 內必有一個實根。
內必有一個實根。
即方程.files/image235.gif) 必有一個實數根屬于
必有一個實數根屬于.files/image237.gif) 。------------8分
。------------8分
(3)假設.files/image248.gif) 存在,由①得
存在,由①得.files/image522.gif)
.files/image524.gif)
.files/image526.gif)
由②知對.files/image054.gif) ,都有
,都有.files/image246.gif)
令.files/image290.gif) 得
得.files/image529.gif)
.files/image531.gif)
.files/image533.gif)
.files/image535.gif)
由.files/image537.gif) 得
得.files/image539.gif) ,
,
當.files/image539.gif) 時,
時,.files/image541.gif) ,其頂點為(-1,0)滿足條件①,又
,其頂點為(-1,0)滿足條件①,又.files/image543.gif)
.files/image524.gif) 對
對.files/image054.gif) ,都有
,都有.files/image246.gif) ,滿足條件②。
,滿足條件②。
∴存在.files/image239.gif) ,使
,使.files/image170.gif) 同時滿足條件①、②。------------------------------14分
同時滿足條件①、②。------------------------------14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com