
題目列表(包括答案和解析)
拋物線 上一點(diǎn)
上一點(diǎn) 到焦點(diǎn)的距離為3,則點(diǎn)
到焦點(diǎn)的距離為3,則點(diǎn) 的橫坐標(biāo)是 .
的橫坐標(biāo)是 .
拋物線 上一點(diǎn)
上一點(diǎn) 到焦點(diǎn)的距離為3,則點(diǎn)
到焦點(diǎn)的距離為3,則點(diǎn) 的橫坐標(biāo)
的橫坐標(biāo) .
.
拋物線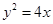 上一點(diǎn)
上一點(diǎn)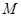 到焦點(diǎn)的距離為3,則點(diǎn)
到焦點(diǎn)的距離為3,則點(diǎn)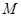 的橫坐標(biāo)
的橫坐標(biāo)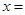 .
.
拋物線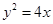 上一點(diǎn)
上一點(diǎn)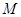 到焦點(diǎn)的距離為3,則點(diǎn)
到焦點(diǎn)的距離為3,則點(diǎn)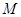 的橫坐標(biāo)
的橫坐標(biāo)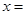 .
.
拋物線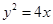 上一點(diǎn)
上一點(diǎn) 到焦點(diǎn)的距離為3,則點(diǎn)
到焦點(diǎn)的距離為3,則點(diǎn) 的橫坐標(biāo)是 .
的橫坐標(biāo)是 .
說(shuō)明:1.參考答案與評(píng)分標(biāo)準(zhǔn)指出了每道題要考查的主要知識(shí)和能力,并給出了一種或幾種解法供參考,如果考生的解法與參考答案不同,可根據(jù)試題主要考查的知識(shí)點(diǎn)和能力比照評(píng)分標(biāo)準(zhǔn)給以相應(yīng)的分?jǐn)?shù).
2.對(duì)解答題中的計(jì)算題,當(dāng)考生的解答在某一步出現(xiàn)錯(cuò)誤時(shí),如果后繼部分的解答未改變?cè)擃}的內(nèi)容和難度,可視影響的程度決定后繼部分的得分,但所給分?jǐn)?shù)不得超過(guò)該部分正確解答應(yīng)得分?jǐn)?shù)的一半;如果后繼部分的解答有較嚴(yán)重的錯(cuò)誤,就不再給分.
3.解答右端所注分?jǐn)?shù),表示考生正確做到這一步應(yīng)得的累加分?jǐn)?shù).
4.只給整數(shù)分?jǐn)?shù),選擇題和填空題不給中間分.
一、選擇題:本大題主要考查基本知識(shí)和基本運(yùn)算.共10小題,每小題5分,滿分50分.
題號(hào)
1
2
3
4
5
6
7
8
9
10
答案
B
D
D
C
B
A
D
A
C
B
10.方法1:由學(xué)調(diào)研測(cè)試試題(文科).files/image128.gif) ,得
,得學(xué)調(diào)研測(cè)試試題(文科).files/image280.gif) ,
,
即學(xué)調(diào)研測(cè)試試題(文科).files/image282.gif) .
.
于是學(xué)調(diào)研測(cè)試試題(文科).files/image284.gif) ,
,
所以學(xué)調(diào)研測(cè)試試題(文科).files/image286.gif) .
.
方法2:由學(xué)調(diào)研測(cè)試試題(文科).files/image128.gif) ,得
,得學(xué)調(diào)研測(cè)試試題(文科).files/image280.gif) ,
,
即學(xué)調(diào)研測(cè)試試題(文科).files/image282.gif) .
.
于是學(xué)調(diào)研測(cè)試試題(文科).files/image288.gif) ,
,
則學(xué)調(diào)研測(cè)試試題(文科).files/image290.gif) (其中
(其中學(xué)調(diào)研測(cè)試試題(文科).files/image292.gif) ),再利用導(dǎo)數(shù)的方法求解.
),再利用導(dǎo)數(shù)的方法求解.
二、填空題:本大題主要考查基本知識(shí)和基本運(yùn)算.共5小題,每小題5分,滿分20分.
11.760 12.12
13.3;-1
14.學(xué)調(diào)研測(cè)試試題(文科).files/image294.gif) 15.3
15.3
三、解答題:本大題共6小題,滿分80分.解答須寫出文字說(shuō)明、證明過(guò)程和演算步驟.
16.(本小題滿分12分)
(本小題主要考查互斥事件等基礎(chǔ)知識(shí),考查運(yùn)算求解能力)
解:記“甲射擊一次,命中7環(huán)以下”為事件學(xué)調(diào)研測(cè)試試題(文科).files/image008.gif) ,“甲射擊一次,命中7環(huán)”為事件
,“甲射擊一次,命中7環(huán)”為事件學(xué)調(diào)研測(cè)試試題(文科).files/image010.gif) ,由于在一次射擊中,
,由于在一次射擊中,學(xué)調(diào)研測(cè)試試題(文科).files/image008.gif) 與
與學(xué)調(diào)研測(cè)試試題(文科).files/image010.gif) 不可能同時(shí)發(fā)生,故
不可能同時(shí)發(fā)生,故學(xué)調(diào)研測(cè)試試題(文科).files/image008.gif) 與
與學(xué)調(diào)研測(cè)試試題(文科).files/image010.gif) 是互斥事件,
是互斥事件,
(1)“甲射擊一次,命中不足8環(huán)”的事件為學(xué)調(diào)研測(cè)試試題(文科).files/image298.gif) ,
,
由互斥事件的概率加法公式,學(xué)調(diào)研測(cè)試試題(文科).files/image300.gif) .
.
答:甲射擊一次,命中不足8環(huán)的概率是0.22.…………………………………6分
(2)方法1:記“甲射擊一次,命中8環(huán)”為事件學(xué)調(diào)研測(cè)試試題(文科).files/image238.gif) ,“甲射擊一次,命中9環(huán)(含9環(huán))以上”為事件
,“甲射擊一次,命中9環(huán)(含9環(huán))以上”為事件學(xué)調(diào)研測(cè)試試題(文科).files/image240.gif) ,則“甲射擊一次,至少命中7環(huán)”的事件為
,則“甲射擊一次,至少命中7環(huán)”的事件為學(xué)調(diào)研測(cè)試試題(文科).files/image304.gif) ,
,
∴學(xué)調(diào)研測(cè)試試題(文科).files/image306.gif) .
.
答:甲射擊一次,至少命中7環(huán)的概率為0.9.…………………………………12分
方法2:∵“甲射擊一次,至少命中7環(huán)”為事件學(xué)調(diào)研測(cè)試試題(文科).files/image308.gif) ,
,
∴學(xué)調(diào)研測(cè)試試題(文科).files/image310.gif) =1-0.1=0.9.
=1-0.1=0.9.
答:甲射擊一次,至少命中7環(huán)的概率為0.9.…………………………………12分
17.(本小題滿分12分)
(本小題主要考查正弦定理、余弦定理、解三角形等基礎(chǔ)知識(shí),考查運(yùn)算求解能力)
解:(1)由余弦定理,學(xué)調(diào)研測(cè)試試題(文科).files/image312.gif) ,………………………………………2分
,………………………………………2分
得學(xué)調(diào)研測(cè)試試題(文科).files/image314.gif) ,…………………………………………………4分
,…………………………………………………4分
學(xué)調(diào)研測(cè)試試題(文科).files/image316.gif)
學(xué)調(diào)研測(cè)試試題(文科).files/image318.gif) .……………………………………………………………………………6分
.……………………………………………………………………………6分
(2)方法1:由余弦定理,得學(xué)調(diào)研測(cè)試試題(文科).files/image320.gif) ,………………………………8分
,………………………………8分
學(xué)調(diào)研測(cè)試試題(文科).files/image322.gif) ,………………………10分
,………………………10分
∵學(xué)調(diào)研測(cè)試試題(文科).files/image238.gif) 是
是學(xué)調(diào)研測(cè)試試題(文科).files/image325.gif) 的內(nèi)角,
的內(nèi)角,
∴學(xué)調(diào)研測(cè)試試題(文科).files/image327.gif) .………………………………………………………12分
.………………………………………………………12分
方法2:∵學(xué)調(diào)研測(cè)試試題(文科).files/image197.gif) ,且
,且學(xué)調(diào)研測(cè)試試題(文科).files/image010.gif) 是
是學(xué)調(diào)研測(cè)試試題(文科).files/image325.gif) 的內(nèi)角,
的內(nèi)角,
∴學(xué)調(diào)研測(cè)試試題(文科).files/image331.gif) .………………………………………………………8分
.………………………………………………………8分
根據(jù)正弦定理,學(xué)調(diào)研測(cè)試試題(文科).files/image333.gif) ,……………………………………………………10分
,……………………………………………………10分
得學(xué)調(diào)研測(cè)試試題(文科).files/image335.gif) . ……………………………………………12分
. ……………………………………………12分
18.(本小題滿分14分)
(本小題主要考查空間中線面關(guān)系,考查數(shù)形結(jié)合的數(shù)學(xué)思想和方法,以及空間想象能力、邏輯推理能力和運(yùn)算求解能力)
學(xué)調(diào)研測(cè)試試題(文科).files/image336.gif) (1)證法1:如圖,取
(1)證法1:如圖,取學(xué)調(diào)研測(cè)試試題(文科).files/image338.gif) 的中點(diǎn)
的中點(diǎn)學(xué)調(diào)研測(cè)試試題(文科).files/image340.gif) ,連接
,連接學(xué)調(diào)研測(cè)試試題(文科).files/image342.gif) ,
,
∵學(xué)調(diào)研測(cè)試試題(文科).files/image344.gif) 分別為
分別為學(xué)調(diào)研測(cè)試試題(文科).files/image346.gif) 的中點(diǎn),∴
的中點(diǎn),∴學(xué)調(diào)研測(cè)試試題(文科).files/image348.gif) .
.
∵學(xué)調(diào)研測(cè)試試題(文科).files/image350.gif) 分別為
分別為學(xué)調(diào)研測(cè)試試題(文科).files/image352.gif) 的中點(diǎn),∴
的中點(diǎn),∴學(xué)調(diào)研測(cè)試試題(文科).files/image354.gif) .
.
∴學(xué)調(diào)研測(cè)試試題(文科).files/image356.gif)
學(xué)調(diào)研測(cè)試試題(文科).files/image358.gif) .
.
∴學(xué)調(diào)研測(cè)試試題(文科).files/image360.gif) 四點(diǎn)共面.………………………………………………………………2分
四點(diǎn)共面.………………………………………………………………2分
∵學(xué)調(diào)研測(cè)試試題(文科).files/image362.gif) 分別為
分別為學(xué)調(diào)研測(cè)試試題(文科).files/image364.gif) 的中點(diǎn),∴
的中點(diǎn),∴學(xué)調(diào)研測(cè)試試題(文科).files/image366.gif) .……………………………………4分
.……………………………………4分
∵學(xué)調(diào)研測(cè)試試題(文科).files/image368.gif) 平面
平面學(xué)調(diào)研測(cè)試試題(文科).files/image223.gif) ,
,學(xué)調(diào)研測(cè)試試題(文科).files/image371.gif) 平面
平面學(xué)調(diào)研測(cè)試試題(文科).files/image223.gif) ,
,
∴學(xué)調(diào)研測(cè)試試題(文科).files/image221.gif) 平面
平面學(xué)調(diào)研測(cè)試試題(文科).files/image223.gif) .……………………………………………………………………6分
.……………………………………………………………………6分
證法2:∵學(xué)調(diào)研測(cè)試試題(文科).files/image374.gif) 分別為
分別為學(xué)調(diào)研測(cè)試試題(文科).files/image376.gif) 的中點(diǎn),
的中點(diǎn),
∴學(xué)調(diào)研測(cè)試試題(文科).files/image348.gif) ,
,學(xué)調(diào)研測(cè)試試題(文科).files/image378.gif) .……………………………………………………………2分
.……………………………………………………………2分
∵學(xué)調(diào)研測(cè)試試題(文科).files/image380.gif) ,∴
,∴學(xué)調(diào)研測(cè)試試題(文科).files/image382.gif) .
.
∵學(xué)調(diào)研測(cè)試試題(文科).files/image384.gif) ,
,學(xué)調(diào)研測(cè)試試題(文科).files/image386.gif) ,∴平面
,∴平面學(xué)調(diào)研測(cè)試試題(文科).files/image388.gif) 平面
平面學(xué)調(diào)研測(cè)試試題(文科).files/image390.gif) . …………………5分
. …………………5分
∵學(xué)調(diào)研測(cè)試試題(文科).files/image392.gif) 平面
平面學(xué)調(diào)研測(cè)試試題(文科).files/image390.gif) ,∴
,∴學(xué)調(diào)研測(cè)試試題(文科).files/image221.gif) 平面
平面學(xué)調(diào)研測(cè)試試題(文科).files/image223.gif) . …………………………………………6分
. …………………………………………6分
(2)解:∵學(xué)調(diào)研測(cè)試試題(文科).files/image208.gif) 平面
平面學(xué)調(diào)研測(cè)試試題(文科).files/image206.gif) ,
,學(xué)調(diào)研測(cè)試試題(文科).files/image397.gif) 平面
平面學(xué)調(diào)研測(cè)試試題(文科).files/image206.gif) ,∴
,∴學(xué)調(diào)研測(cè)試試題(文科).files/image399.gif) .
.
∵學(xué)調(diào)研測(cè)試試題(文科).files/image206.gif) 為正方形,∴
為正方形,∴學(xué)調(diào)研測(cè)試試題(文科).files/image401.gif) .
.
∵學(xué)調(diào)研測(cè)試試題(文科).files/image403.gif) ,∴
,∴學(xué)調(diào)研測(cè)試試題(文科).files/image405.gif) 平面
平面學(xué)調(diào)研測(cè)試試題(文科).files/image407.gif) .……………………………………………8分
.……………………………………………8分
∵學(xué)調(diào)研測(cè)試試題(文科).files/image409.gif) ,
,學(xué)調(diào)研測(cè)試試題(文科).files/image411.gif) ,∴
,∴學(xué)調(diào)研測(cè)試試題(文科).files/image413.gif) .……………10分
.……………10分
∵學(xué)調(diào)研測(cè)試試題(文科).files/image415.gif) ,
,
∴學(xué)調(diào)研測(cè)試試題(文科).files/image417.gif) .…………………………………14分
.…………………………………14分
19.(本小題滿分14分)
(本小題主要考查橢圓方程的定義等基礎(chǔ)知識(shí),考查分類與整合、數(shù)形結(jié)合的數(shù)學(xué)思想方法,以及抽象概括能力、運(yùn)算求解能力)
解:(1)根據(jù)橢圓的定義,可知?jiǎng)狱c(diǎn)學(xué)調(diào)研測(cè)試試題(文科).files/image056.gif) 的軌跡為橢圓,………………………………1分
的軌跡為橢圓,………………………………1分
其中學(xué)調(diào)研測(cè)試試題(文科).files/image193.gif) ,
,學(xué)調(diào)研測(cè)試試題(文科).files/image421.gif) ,則
,則學(xué)調(diào)研測(cè)試試題(文科).files/image423.gif) .………………………………………2分
.………………………………………2分
所以動(dòng)點(diǎn)M的軌跡方程為學(xué)調(diào)研測(cè)試試題(文科).files/image425.gif) .………………………………………………4分
.………………………………………………4分
(2)當(dāng)直線學(xué)調(diào)研測(cè)試試題(文科).files/image236.gif) 的斜率不存在時(shí),不滿足題意.………………………………………5分
的斜率不存在時(shí),不滿足題意.………………………………………5分
當(dāng)直線學(xué)調(diào)研測(cè)試試題(文科).files/image236.gif) 的斜率存在時(shí),設(shè)直線
的斜率存在時(shí),設(shè)直線學(xué)調(diào)研測(cè)試試題(文科).files/image236.gif) 的方程為
的方程為學(xué)調(diào)研測(cè)試試題(文科).files/image427.gif) ,設(shè)
,設(shè)學(xué)調(diào)研測(cè)試試題(文科).files/image429.gif) ,
,學(xué)調(diào)研測(cè)試試題(文科).files/image431.gif) ,
,
∵學(xué)調(diào)研測(cè)試試題(文科).files/image242.gif) ,∴
,∴學(xué)調(diào)研測(cè)試試題(文科).files/image434.gif) .……………………………………………7分
.……………………………………………7分
∵學(xué)調(diào)研測(cè)試試題(文科).files/image436.gif) ,
,學(xué)調(diào)研測(cè)試試題(文科).files/image438.gif) ,
,
∴學(xué)調(diào)研測(cè)試試題(文科).files/image440.gif) .
.
∴ 學(xué)調(diào)研測(cè)試試題(文科).files/image442.gif) .………… ① …………………………9分
.………… ① …………………………9分
由方程組學(xué)調(diào)研測(cè)試試題(文科).files/image444.gif)
得學(xué)調(diào)研測(cè)試試題(文科).files/image446.gif) .…………………………………………………11分
.…………………………………………………11分
則學(xué)調(diào)研測(cè)試試題(文科).files/image448.gif) ,
,學(xué)調(diào)研測(cè)試試題(文科).files/image450.gif) ,
,
代入①,得學(xué)調(diào)研測(cè)試試題(文科).files/image452.gif) .
.
即學(xué)調(diào)研測(cè)試試題(文科).files/image454.gif) ,解得,
,解得,學(xué)調(diào)研測(cè)試試題(文科).files/image456.gif) 或
或學(xué)調(diào)研測(cè)試試題(文科).files/image458.gif) .………………………………………………13分
.………………………………………………13分
所以,直線學(xué)調(diào)研測(cè)試試題(文科).files/image236.gif) 的方程是
的方程是學(xué)調(diào)研測(cè)試試題(文科).files/image460.gif) 或
或學(xué)調(diào)研測(cè)試試題(文科).files/image462.gif) .………………………………14分
.………………………………14分
20.(本小題滿分14分)
(本小題主要考查函數(shù)與導(dǎo)數(shù)的概念、不等式及其性質(zhì)等基礎(chǔ)知識(shí),考查分類討論、化歸與轉(zhuǎn)化、數(shù)形結(jié)合的數(shù)學(xué)思想方法,以及抽象概括能力、邏輯推理能力、運(yùn)算求解能力和創(chuàng)新意識(shí))
解:(1)∵學(xué)調(diào)研測(cè)試試題(文科).files/image464.gif) ,且
,且學(xué)調(diào)研測(cè)試試題(文科).files/image466.gif) ,…………………………………1分
,…………………………………1分
當(dāng)學(xué)調(diào)研測(cè)試試題(文科).files/image468.gif) 時(shí),得
時(shí),得學(xué)調(diào)研測(cè)試試題(文科).files/image470.gif) ;當(dāng)
;當(dāng)學(xué)調(diào)研測(cè)試試題(文科).files/image472.gif) 時(shí),得
時(shí),得學(xué)調(diào)研測(cè)試試題(文科).files/image474.gif) ;
;
∴學(xué)調(diào)研測(cè)試試題(文科).files/image248.gif) 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為學(xué)調(diào)研測(cè)試試題(文科).files/image477.gif) ;
;
學(xué)調(diào)研測(cè)試試題(文科).files/image248.gif) 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為學(xué)調(diào)研測(cè)試試題(文科).files/image480.gif) 和
和學(xué)調(diào)研測(cè)試試題(文科).files/image482.gif) .…………………………………3分
.…………………………………3分
故當(dāng)學(xué)調(diào)研測(cè)試試題(文科).files/image484.gif) 時(shí),
時(shí),學(xué)調(diào)研測(cè)試試題(文科).files/image248.gif) 有極大值,其極大值為
有極大值,其極大值為學(xué)調(diào)研測(cè)試試題(文科).files/image486.gif) . …………………4分
. …………………4分
(2)∵學(xué)調(diào)研測(cè)試試題(文科).files/image488.gif) ,
,
當(dāng)學(xué)調(diào)研測(cè)試試題(文科).files/image490.gif) 時(shí),
時(shí),學(xué)調(diào)研測(cè)試試題(文科).files/image492.gif) ,
,
∴學(xué)調(diào)研測(cè)試試題(文科).files/image494.gif) 在區(qū)間
在區(qū)間學(xué)調(diào)研測(cè)試試題(文科).files/image496.gif) 內(nèi)是單調(diào)遞減.…………………………………………6分
內(nèi)是單調(diào)遞減.…………………………………………6分
∴學(xué)調(diào)研測(cè)試試題(文科).files/image498.gif) .
.
∵學(xué)調(diào)研測(cè)試試題(文科).files/image252.gif) ,∴
,∴學(xué)調(diào)研測(cè)試試題(文科).files/image500.gif)
此時(shí),學(xué)調(diào)研測(cè)試試題(文科).files/image502.gif) .…………………………………………………………………………9分
.…………………………………………………………………………9分
當(dāng)學(xué)調(diào)研測(cè)試試題(文科).files/image504.gif) 時(shí),
時(shí),學(xué)調(diào)研測(cè)試試題(文科).files/image506.gif) .
.
∵學(xué)調(diào)研測(cè)試試題(文科).files/image252.gif) ,∴
,∴學(xué)調(diào)研測(cè)試試題(文科).files/image508.gif) 即
即學(xué)調(diào)研測(cè)試試題(文科).files/image510.gif) ……11分
……11分
此時(shí),學(xué)調(diào)研測(cè)試試題(文科).files/image512.gif) .……………………………………………………………13分
.……………………………………………………………13分
綜上可知,實(shí)數(shù)學(xué)調(diào)研測(cè)試試題(文科).files/image514.gif) 的取值范圍為
的取值范圍為學(xué)調(diào)研測(cè)試試題(文科).files/image516.gif) .…………………………………14分
.…………………………………14分
21.(本小題滿分14分)
(本小題主要考查等差數(shù)列、不等式及其性質(zhì)等基礎(chǔ)知識(shí),考查分類討論、化歸與轉(zhuǎn)化的數(shù)學(xué)思想方法,以及抽象概括能力、運(yùn)算求解能力)
解:(1)由已知,學(xué)調(diào)研測(cè)試試題(文科).files/image518.gif) (
(學(xué)調(diào)研測(cè)試試題(文科).files/image269.gif) ,
,學(xué)調(diào)研測(cè)試試題(文科).files/image271.gif) ), …………………2分
), …………………2分
即學(xué)調(diào)研測(cè)試試題(文科).files/image520.gif) (
(學(xué)調(diào)研測(cè)試試題(文科).files/image269.gif) ,
,學(xué)調(diào)研測(cè)試試題(文科).files/image271.gif) ),且
),且學(xué)調(diào)研測(cè)試試題(文科).files/image522.gif) .
.
∴數(shù)列學(xué)調(diào)研測(cè)試試題(文科).files/image258.gif) 是以
是以學(xué)調(diào)研測(cè)試試題(文科).files/image260.gif) 為首項(xiàng),公差為1的等差數(shù)列.
為首項(xiàng),公差為1的等差數(shù)列.
∴學(xué)調(diào)研測(cè)試試題(文科).files/image525.gif) .……………………………………………………………………………4分
.……………………………………………………………………………4分
(2)∵學(xué)調(diào)研測(cè)試試題(文科).files/image525.gif) ,∴
,∴學(xué)調(diào)研測(cè)試試題(文科).files/image528.gif) ,要使
,要使學(xué)調(diào)研測(cè)試試題(文科).files/image277.gif) 恒成立,
恒成立,
∴學(xué)調(diào)研測(cè)試試題(文科).files/image530.gif) 恒成立,
恒成立,
∴學(xué)調(diào)研測(cè)試試題(文科).files/image532.gif) 恒成立,
恒成立,
∴學(xué)調(diào)研測(cè)試試題(文科).files/image534.gif) 恒成立.……………………………………………………………6分
恒成立.……………………………………………………………6分
(?)當(dāng)學(xué)調(diào)研測(cè)試試題(文科).files/image094.gif) 為奇數(shù)時(shí),即
為奇數(shù)時(shí),即學(xué)調(diào)研測(cè)試試題(文科).files/image537.gif) 恒成立,…………………………………………7分
恒成立,…………………………………………7分
當(dāng)且僅當(dāng)學(xué)調(diào)研測(cè)試試題(文科).files/image539.gif) 時(shí),
時(shí),學(xué)調(diào)研測(cè)試試題(文科).files/image541.gif) 有最小值為1,
有最小值為1,
∴學(xué)調(diào)研測(cè)試試題(文科).files/image543.gif) .………………………………………………………………………………9分
.………………………………………………………………………………9分
(?)當(dāng)學(xué)調(diào)研測(cè)試試題(文科).files/image094.gif) 為偶數(shù)時(shí),即
為偶數(shù)時(shí),即學(xué)調(diào)研測(cè)試試題(文科).files/image546.gif) 恒成立,………………………………………10分
恒成立,………………………………………10分
當(dāng)且僅當(dāng)學(xué)調(diào)研測(cè)試試題(文科).files/image548.gif) 時(shí),
時(shí),學(xué)調(diào)研測(cè)試試題(文科).files/image550.gif) 有最大值
有最大值學(xué)調(diào)研測(cè)試試題(文科).files/image552.gif) ,
,
∴學(xué)調(diào)研測(cè)試試題(文科).files/image554.gif) .……………………………………………………………………………12分
.……………………………………………………………………………12分
即學(xué)調(diào)研測(cè)試試題(文科).files/image556.gif) ,又
,又學(xué)調(diào)研測(cè)試試題(文科).files/image275.gif) 為非零整數(shù),則
為非零整數(shù),則學(xué)調(diào)研測(cè)試試題(文科).files/image559.gif) .
.
綜上所述,存在學(xué)調(diào)研測(cè)試試題(文科).files/image559.gif) ,使得對(duì)任意
,使得對(duì)任意學(xué)調(diào)研測(cè)試試題(文科).files/image271.gif) ,都有
,都有學(xué)調(diào)研測(cè)試試題(文科).files/image562.gif) .…………………14分
.…………………14分
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com