
題目列表(包括答案和解析)
設(shè)△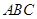 的內(nèi)角
的內(nèi)角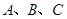 所對邊的長分別為
所對邊的長分別為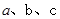 ,且有
,且有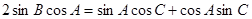
(Ⅰ)求角A的大小;
(Ⅱ)若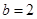 ,
,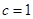 ,
,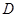 為
為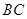 的中點,求
的中點,求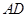 的長。
的長。
【解析】(1)由題,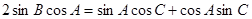 ,則
,則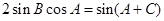 ,故
,故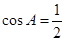 ,即
,即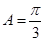 .
.
(2)因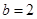 ,
,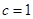 ,因
,因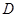 為
為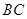 的中點,故
的中點,故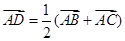 ,則
,則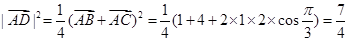 ,所以
,所以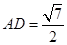
已知函數(shù) (
( 為實數(shù)).
為實數(shù)).
(Ⅰ)當 時,求
時,求 的最小值;
的最小值;
(Ⅱ)若 在
在 上是單調(diào)函數(shù),求
上是單調(diào)函數(shù),求 的取值范圍.
的取值范圍.
【解析】第一問中由題意可知: . ∵
. ∵ ∴
∴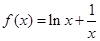 ∴
∴
 .
.
當 時,
時, ;
當
;
當 時,
時, . 故
. 故 .
.
第二問
 .
.
當 時,
時, ,在
,在 上有
上有 ,
, 遞增,符合題意;
遞增,符合題意;
令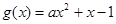 ,則
,則
 ,∴
,∴ 或
或 在
在 上恒成立.轉(zhuǎn)化后解決最值即可。
上恒成立.轉(zhuǎn)化后解決最值即可。
解:(Ⅰ) 由題意可知: . ∵
. ∵ ∴
∴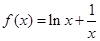 ∴
∴
 .
.
當 時,
時, ;
當
;
當 時,
時, . 故
. 故 .
.
(Ⅱ) 
 .
.
當 時,
時, ,在
,在 上有
上有 ,
, 遞增,符合題意;
遞增,符合題意;
令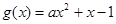 ,則
,則
 ,∴
,∴ 或
或 在
在 上恒成立.∵二次函數(shù)
上恒成立.∵二次函數(shù)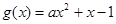 的對稱軸為
的對稱軸為 ,且
,且
∴ 或
或
 或
或
 或
或
 或
或 . 綜上
. 綜上
已知橢圓
 的離心率為
的離心率為 ,以原點為圓心,橢圓的短半軸長為半徑的圓與直線
,以原點為圓心,橢圓的短半軸長為半徑的圓與直線 相切.
相切.
(I)求橢圓 的方程;
的方程;
(II)若過點 (2,0)的直線與橢圓
(2,0)的直線與橢圓 相交于兩點
相交于兩點 ,設(shè)
,設(shè) 為橢圓上一點,且滿足
為橢圓上一點,且滿足 (O為坐標原點),當
(O為坐標原點),當 <
< 時,求實數(shù)
時,求實數(shù) 的取值范圍.
的取值范圍.
【解析】本試題主要考查了橢圓的方程以及直線與橢圓的位置關(guān)系的運用。
第一問中,利用
第二問中,利用直線與橢圓聯(lián)系,可知得到一元二次方程中 ,可得k的范圍,然后利用向量的
,可得k的范圍,然后利用向量的 <
< 不等式,表示得到t的范圍。
不等式,表示得到t的范圍。
解:(1)由題意知

已知函數(shù) 在
在 取得極值
取得極值
(1)求 的單調(diào)區(qū)間(用
的單調(diào)區(qū)間(用 表示);
表示);
(2)設(shè) ,
, ,若存在
,若存在 ,使得
,使得 成立,求
成立,求 的取值范圍.
的取值范圍.
【解析】第一問利用

根據(jù)題意 在
在 取得極值,
取得極值, 
對參數(shù)a分情況討論,可知
當 即
即 時遞增區(qū)間:
時遞增區(qū)間:  遞減區(qū)間:
遞減區(qū)間:  ,
,

當 即
即 時遞增區(qū)間:
時遞增區(qū)間:  遞減區(qū)間:
遞減區(qū)間:  ,
,

第二問中, 由(1)知:
由(1)知:  在
在 ,
,

 ,
,
 在
在


從而求解。
解: 
 …..3分
…..3分
 在
在 取得極值,
取得極值,  ……………………..4分
……………………..4分
(1) 當 即
即 時 遞增區(qū)間:
時 遞增區(qū)間:  遞減區(qū)間:
遞減區(qū)間:  ,
,

當 即
即 時遞增區(qū)間:
時遞增區(qū)間:  遞減區(qū)間:
遞減區(qū)間:  ,
,
 ………….6分
………….6分
(2)  由(1)知:
由(1)知:  在
在 ,
,

 ,
,
 在
在

 ……………….10分
……………….10分
 , 使
, 使 成立
成立



 得:
得: 
設(shè)A是由m×n個實數(shù)組成的m行n列的數(shù)表,滿足:每個數(shù)的絕對值不大于1,且所有數(shù)的和為零,記s(m,n)為所有這樣的數(shù)表構(gòu)成的集合。
對于A∈S(m,n),記ri(A)為A的第ⅰ行各數(shù)之和(1≤ⅰ≤m),Cj(A)為A的第j列各數(shù)之和(1≤j≤n):
記K(A)為∣r1(A)∣,∣R2(A)∣,…,∣Rm(A)∣,∣C1(A)∣,∣C2(A)∣,…,∣Cn(A)∣中的最小值。
(1) 對如下數(shù)表A,求K(A)的值;
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
(2)設(shè)數(shù)表A∈S(2,3)形如
|
1 |
1 |
c |
|
a |
b |
-1 |
求K(A)的最大值;
(3)給定正整數(shù)t,對于所有的A∈S(2,2t+1),求K(A)的最大值。
【解析】(1)因為 ,
,
所以
(2) 不妨設(shè) .由題意得
.由題意得 .又因為
.又因為 ,所以
,所以 ,
,
于是 ,
, ,
,

所以 ,當
,當 ,且
,且 時,
時, 取得最大值1。
取得最大值1。
(3)對于給定的正整數(shù)t,任給數(shù)表 如下,
如下,
|
|
|
… |
|
|
|
|
… |
|
任意改變A的行次序或列次序,或把A中的每一個數(shù)換成它的相反數(shù),所得數(shù)表
 ,并且
,并且 ,因此,不妨設(shè)
,因此,不妨設(shè) ,
,
且
 。
。
由 得定義知,
得定義知, ,
,

又因為
所以


所以,
對數(shù)表 :
:
|
1 |
1 |
… |
1 |
|
… |
|
|
|
|
… |
|
-1 |
… |
-1 |
則 且
且 ,
,
綜上,對于所有的 ,
, 的最大值為
的最大值為
國際學(xué)校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com