
題目列表(包括答案和解析)
設數列 的各項均為正數.若對任意的
的各項均為正數.若對任意的 ,存在
,存在 ,使得
,使得 成立,則稱數列
成立,則稱數列 為“Jk型”數列.
為“Jk型”數列.
(1)若數列 是“J2型”數列,且
是“J2型”數列,且 ,
, ,求
,求 ;
;
(2)若數列 既是“J3型”數列,又是“J4型”數列,證明:數列
既是“J3型”數列,又是“J4型”數列,證明:數列 是等比數列.
是等比數列.
【解析】1)中由題意,得 ,
, ,
, ,
, ,…成等比數列,且公比
,…成等比數列,且公比 ,
,
所以.
(2)中證明:由{ }是“j4型”數列,得
}是“j4型”數列,得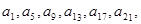 ,…成等比數列,設公比為t. 由{
,…成等比數列,設公比為t. 由{ }是“j3型”數列,得
}是“j3型”數列,得
 ,…成等比數列,設公比為
,…成等比數列,設公比為 ;
;
 ,…成等比數列,設公比為
,…成等比數列,設公比為 ;
;
 …成等比數列,設公比為
…成等比數列,設公比為 ;
;
已知函數 (
( 為實數).
為實數).
(Ⅰ)當 時,求
時,求 的最小值;
的最小值;
(Ⅱ)若 在
在 上是單調函數,求
上是單調函數,求 的取值范圍.
的取值范圍.
【解析】第一問中由題意可知: . ∵
. ∵ ∴
∴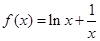 ∴
∴
 .
.
當 時,
時, ;
當
;
當 時,
時, . 故
. 故 .
.
第二問
 .
.
當 時,
時, ,在
,在 上有
上有 ,
, 遞增,符合題意;
遞增,符合題意;
令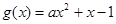 ,則
,則
 ,∴
,∴ 或
或 在
在 上恒成立.轉化后解決最值即可。
上恒成立.轉化后解決最值即可。
解:(Ⅰ) 由題意可知: . ∵
. ∵ ∴
∴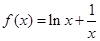 ∴
∴
 .
.
當 時,
時, ;
當
;
當 時,
時, . 故
. 故 .
.
(Ⅱ) 
 .
.
當 時,
時, ,在
,在 上有
上有 ,
, 遞增,符合題意;
遞增,符合題意;
令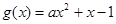 ,則
,則
 ,∴
,∴ 或
或 在
在 上恒成立.∵二次函數
上恒成立.∵二次函數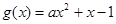 的對稱軸為
的對稱軸為 ,且
,且
∴ 或
或
 或
或
 或
或
 或
或 . 綜上
. 綜上
若函數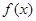 在定義域內存在區間
在定義域內存在區間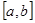 ,滿足
,滿足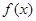 在
在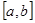 上的值域為
上的值域為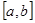 ,則稱這樣的函數
,則稱這樣的函數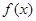 為“優美函數”.
為“優美函數”.
(Ⅰ)判斷函數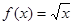 是否為“優美函數”?若是,求出
是否為“優美函數”?若是,求出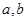 ;若不是,說明理由;
;若不是,說明理由;
(Ⅱ)若函數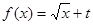 為“優美函數”,求實數
為“優美函數”,求實數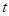 的取值范圍.
的取值范圍.
【解析】第一問中,利用定義,判定由題意得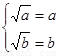 ,由
,由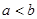 ,所以
,所以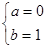
第二問中, 由題意得方程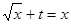 有兩實根
有兩實根
設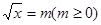 所以關于m的方程
所以關于m的方程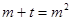 在
在 有兩實根,
有兩實根,
即函數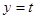 與函數
與函數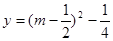 的圖像在
的圖像在 上有兩個不同交點,從而得到t的范圍。
上有兩個不同交點,從而得到t的范圍。
解(I)由題意得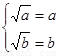 ,由
,由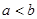 ,所以
,所以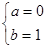 (6分)
(6分)
(II)由題意得方程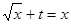 有兩實根
有兩實根
設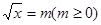 所以關于m的方程
所以關于m的方程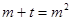 在
在 有兩實根,
有兩實根,
即函數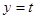 與函數
與函數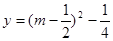 的圖像在
的圖像在 上有兩個不同交點。
上有兩個不同交點。
已知函數 在
在 取得極值
取得極值
(1)求 的單調區間(用
的單調區間(用 表示);
表示);
(2)設 ,
, ,若存在
,若存在 ,使得
,使得 成立,求
成立,求 的取值范圍.
的取值范圍.
【解析】第一問利用

根據題意 在
在 取得極值,
取得極值, 
對參數a分情況討論,可知
當 即
即 時遞增區間:
時遞增區間:  遞減區間:
遞減區間:  ,
,

當 即
即 時遞增區間:
時遞增區間:  遞減區間:
遞減區間:  ,
,

第二問中, 由(1)知:
由(1)知:  在
在 ,
,

 ,
,
 在
在


從而求解。
解: 
 …..3分
…..3分
 在
在 取得極值,
取得極值,  ……………………..4分
……………………..4分
(1) 當 即
即 時 遞增區間:
時 遞增區間:  遞減區間:
遞減區間:  ,
,

當 即
即 時遞增區間:
時遞增區間:  遞減區間:
遞減區間:  ,
,
 ………….6分
………….6分
(2)  由(1)知:
由(1)知:  在
在 ,
,

 ,
,
 在
在

 ……………….10分
……………….10分
 , 使
, 使 成立
成立



 得:
得: 
已知 中,內角
中,內角 的對邊的邊長分別為
的對邊的邊長分別為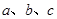 ,且
,且
(I)求角 的大小;
的大小;
(II)若 求
求 的最小值.
的最小值.
【解析】第一問,由正弦定理可得:sinBcosC=2sinAcosB-sinCcosB,即sin(B+C)=2sinAcosB,
第二問,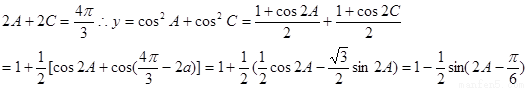
三角函數的性質運用。
解:(Ⅰ)由正弦定理可得:sinBcosC=2sinAcosB-sinCcosB,即sin(B+C)=2sinAcosB,
(Ⅱ)由(Ⅰ)可知
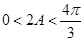 ,
, ,則當
,則當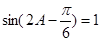 ,即
,即 時,y的最小值為
時,y的最小值為 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com