
題目列表(包括答案和解析)
已知![]() ,
,![]() ,…,
,…,![]() 是首項為1,公比為2 的等比數列,對于
是首項為1,公比為2 的等比數列,對于![]() 的整數
的整數![]() ,數列
,數列![]() ,
,![]() ,…,
,…,![]() 由
由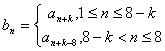 確定,記
確定,記![]() .
.
(Ⅰ)求![]() 時
時![]() 的值(求出具體的數值);
的值(求出具體的數值);
(Ⅱ)求![]() 最小時
最小時![]() 的值.
的值.
(本小題滿分14分)已知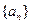 是各項均為正數的等比數列,且
是各項均為正數的等比數列,且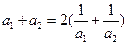 ,
,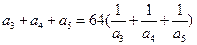
(1)求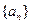 的通項公式;
的通項公式;
(2)設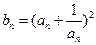 ,求數列
,求數列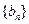 的前
的前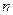 項和
項和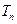 。
。
(3)設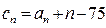 ,求數列{
,求數列{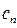 }的前
}的前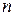 項和最小時
項和最小時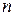 的值。
的值。
(本小題滿分14分)已知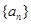 是各項均為正數的等比數列,且
是各項均為正數的等比數列,且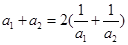 ,
,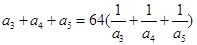
(1)求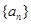 的通項公式;
的通項公式;
(2)設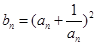 ,求數列
,求數列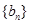 的前
的前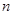 項和
項和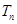 。
。
(3)設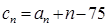 ,求數列{
,求數列{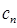 }的前
}的前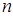 項和最小時
項和最小時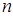 的值。
的值。
已知直線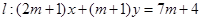 ,圓
,圓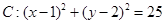
(1)判斷直線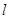 和圓
和圓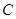 的位置關系;
的位置關系;
(2)若直線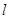 和圓
和圓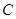 相交,求相交弦長最小時
相交,求相交弦長最小時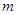 的值.
的值.
(10分)甲、乙兩人玩一種游戲:甲從放有![]() 個紅球、
個紅球、![]() 個白球、
個白球、![]() 個(
個(![]() )黃球的箱子中任取一球,乙從放有5個紅球、3個白球、2個黃球的箱子中任取一球. 規定:當兩球同色時為甲勝,當兩球異色時為乙勝.
)黃球的箱子中任取一球,乙從放有5個紅球、3個白球、2個黃球的箱子中任取一球. 規定:當兩球同色時為甲勝,當兩球異色時為乙勝.
⑴用![]() 表示甲勝的概率;
表示甲勝的概率;
一、選擇題
AACCD BBDDD AC
二、填空題
13. 14.T13 15.①⑤ 16.
14.T13 15.①⑤ 16.
三、解答題
17.解:(Ⅰ)因為 ,
,
由正弦定理,得 ,
……3分
,
……3分
整理,得
因為 、
、 、
、 是
是 的三內角,所以
的三內角,所以 ,
,
因此  .
……6分
.
……6分
(Ⅱ) ,即
,即 ,
……8分
,
……8分
由余弦定理,得 ,所以
,所以 , ……10分
, ……10分
解方程組 ,得
,得 .
……12分
.
……12分
18.(本題滿分12分)
解法一:記 與
與 的比賽為
的比賽為 ,
,
(Ⅰ)齊王與田忌賽馬,有如下六種情況:
 ,
, ,
,
 ,
,  ,
,
 ,
,  . ………………………3分
. ………………………3分
其中田忌獲勝的只有一種 ,所以田忌獲勝的概率為
,所以田忌獲勝的概率為 .
.
…………………………………………………………………………………………6分
(Ⅱ)已知齊王第一場必出上等馬 ,若田忌第一場出上等馬
,若田忌第一場出上等馬 或中等馬
或中等馬 ,則剩下兩場中至少輸掉一場,這時田忌必敗.
,則剩下兩場中至少輸掉一場,這時田忌必敗.
為了使自己獲勝的概率最大,田忌第一場應出下等馬 ,后兩場有兩種情形:
,后兩場有兩種情形:
①若齊王第二場派出中等馬 ,可能對陣情形是
,可能對陣情形是 、
、
或者 、
、 ,所以田忌獲勝的概率為
,所以田忌獲勝的概率為 ; ………………………9分
; ………………………9分
②若齊王第二場派出下等馬 ,可能對陣情形是
,可能對陣情形是 、
、
或者 、
、 ,所以田忌獲勝的概率為
,所以田忌獲勝的概率為 ,
,
所以田忌按 或者
或者 的順序出馬,才能使自己獲勝的概率達到最大值
的順序出馬,才能使自己獲勝的概率達到最大值 .
.
………………………………………………………………………………………12分
解法二:各種對陣情況列成下列表格:



1



2



3



4



5



6



………………………3分
(Ⅰ)其中田忌獲勝的只有第五種這一種情形,所以田忌獲勝的概率為 .……6分
.……6分
(Ⅱ)為了使自己獲勝的概率最大,田忌第一場應出下等馬 ,即只能是第五、第六兩種情形. …………………………………………………9分
,即只能是第五、第六兩種情形. …………………………………………………9分
其中田忌獲勝的只有第五種這一種情形,所以田忌按 或者
或者 的順序出馬,才能使自己獲勝的概率達到最大值
的順序出馬,才能使自己獲勝的概率達到最大值 .………………………12分
.………………………12分
19.(本題滿分12分)
 解證: (Ⅰ) 連結
解證: (Ⅰ) 連結 連結
連結 ,
,
∵四邊形 是矩形
是矩形
∴ 為
為 中點
中點
又 為
為 中點,從而
中點,從而 ∥
∥ ------------3分
------------3分
∵ 平面
平面 ,
, 平面
平面
∴ ∥平面
∥平面 。-----------------------5分
。-----------------------5分
(Ⅱ)(方法1)
三角形 的面積
的面積 -------------------8分
-------------------8分
 到平面
到平面 的距離為
的距離為 的高
的高
∴ ---------------------------------11分
---------------------------------11分
因此,三棱錐 的體積為
的體積為 。------------------------------------12分
。------------------------------------12分
(方法2)

 ,
,
 ,
,
∴ 為等腰
為等腰 ,取底邊
,取底邊 的中點
的中點 ,
,
則 ,
,
∴ 的面積
的面積 -----------8分
-----------8分
∵ ,∴點
,∴點 到平面
到平面 的距離等于
的距離等于 到平面
到平面
 的距離,
的距離,
由于 ,
, ,
,
∴  ,
,
過 作
作 于
于 ,則
,則 就是
就是 到平面
到平面 的距離,
的距離,
又 ,----------11分
,----------11分
 ---------------------12分
---------------------12分
(方法3)
 到平面
到平面 的距離為
的距離為 的高
的高
∴四棱錐 的體積
的體積 ------------------------9分
------------------------9分
三棱錐 的體積
的體積
∴ ---------------------------------------------11分
---------------------------------------------11分
因此,三棱錐 的體積為
的體積為 。-------------------------------------12分
。-------------------------------------12分
20.(Ⅰ)依題意知,
∵ ,
,
∴ .
.
∴所求橢圓 的方程為
的方程為 .
……4分
.
……4分
(Ⅱ)設點
 關于直線
關于直線 的對稱點為
的對稱點為 ,
,
∴  ……6分
……6分
解得: ,
, .
……8分
.
……8分
∴ .
……10分
.
……10分
∵ 點
 在橢圓
在橢圓 :
: 上,
上,
∴ , 則
, 則 .
.
∴ 的取值范圍為
的取值范圍為 .
……12分
.
……12分
21.解:(Ⅰ)由 知,
知, 定義域為
定義域為 ,
,
 . ……………………3分
. ……………………3分
當 時,
時, ,
………………4分
,
………………4分
當 時,
時, .
………………5分
.
………………5分
所以 的單調增區間是
的單調增區間是 ,
,
 的單調減區間是
的單調減區間是 .
…………………… ………………6分
.
…………………… ………………6分
(Ⅱ)由(Ⅰ)知, 在
在 上單調遞增,
上單調遞增,
在 上單調遞減,在
上單調遞減,在 上單調遞增,且當
上單調遞增,且當 或
或 時,
時,
 , 所以
, 所以 的極大值為
的極大值為 ,
,
極小值為 . ………………………8分
. ………………………8分
又因為 ,
,
 , ………10分
, ………10分
所以在 的三個單調區間
的三個單調區間 上,
上,
直線 與
與 的圖象各有一個交點,
的圖象各有一個交點,
當且僅當 , 因此,
, 因此,
 的取值范圍為
的取值范圍為 . ………………12分
. ………………12分
22.解:(Ⅰ)當 時,
時, ……………………………3分
……………………………3分
∴ =
=
=
=
= …………………………………7分
…………………………………7分
(Ⅱ) 

 +
+
 +
+

=
= ……………13分
……………13分
當且僅當 ,即
,即 時,
時, 最小.……………………14分
最小.……………………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com