
題目列表(包括答案和解析)
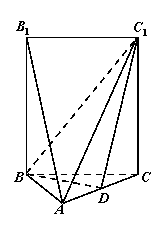
如圖,五面體![]() 中,
中,![]() .底面
.底面![]() 是正三角形,
是正三角形,![]() .四邊形
.四邊形![]() 是矩形,二面角
是矩形,二面角![]() 為直二面角.
為直二面角.
(Ⅰ)![]() 在
在![]() 上運動,當
上運動,當![]() 在何處時,有
在何處時,有![]() ∥平面
∥平面![]() ,并且說明理由;
,并且說明理由;
(Ⅱ)當![]() ∥平面
∥平面![]() 時,求二面角
時,求二面角![]() 余弦值.
余弦值.
 |
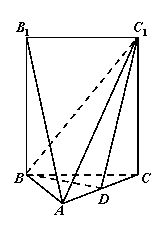
如圖,五面體![]() 中,
中,![]() .底面
.底面![]() 是正三角形,
是正三角形,![]() .四邊形
.四邊形![]() 是矩形,二面角
是矩形,二面角![]() 為直二面角.
為直二面角.
(Ⅰ)若![]() 是
是![]() 中點,求證:
中點,求證:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求該五面體的體積.
 |
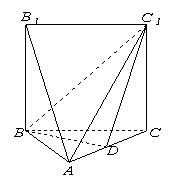
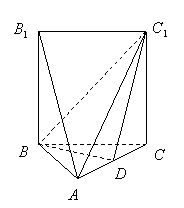 如圖,五面體
如圖,五面體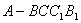 中,
中,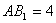 .底面
.底面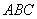 是正三角形,
是正三角形,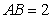 .四邊形
.四邊形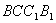 是矩形,平面
是矩形,平面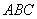
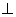 平面
平面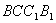
(I)求這個幾何體的體積;
(Ⅱ)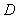 在
在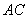 上運動,問:當
上運動,問:當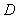 在何處時,有
在何處時,有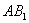 ∥平面
∥平面 ,請說明理由;
,請說明理由;
(III)求二面角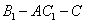 的余弦值.
的余弦值.
如圖,五面體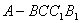 中,
中,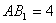 .底面
.底面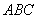 是正三角形,
是正三角形,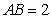 .四邊形
.四邊形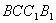 是矩形,二面角
是矩形,二面角 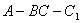 為直二面角.
為直二面角.
(1)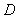 在
在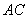 上運動,當
上運動,當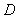 在何處時,有
在何處時,有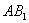 ∥平面
∥平面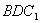 ,并且說明理由;
,并且說明理由;
(2)當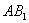 ∥平面
∥平面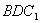 時,求二面角
時,求二面角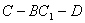 的余弦值.
的余弦值.
(本題14![]() 分)如圖,五面體
分)如圖,五面體![]()
![]() 中
中![]()
![]() ,
,![]() .底面
.底面![]() 是正三角形,
是正三角形,![]() .
.![]() 四邊形
四邊形![]() 是矩形
是矩形![]() ,
,![]() 二面角
二面角![]()
![]() 為直二面角.
為直二面角.
(1)![]() 在
在![]()
![]() 上運動,當
上運動,當![]() 在何處時,有
在何處時,有![]() ∥平面
∥平面![]() ,并且
,并且![]() 說明理由;
說明理由;
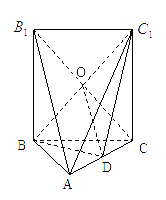
![]()
![]() (2)當
(2)當![]() ∥平面
∥平面![]() 時,求二面角
時,求二面角![]()
![]() 的
的![]() 余弦值.
余弦值.
一、選擇題
AACCD BBDDD AC
二、填空題
13. 14.6 15.①⑤ 16.
14.6 15.①⑤ 16.
三、解答題
17.解:(Ⅰ)因為 ,
,
由正弦定理,得 , ……3分
, ……3分
整理,得
因為 、
、 、
、 是
是 的三內角,所以
的三內角,所以 ,
,
因此  .
……6分
.
……6分