
題目列表(包括答案和解析)
求過點A(5,2)且和直線y=x+5相交成45°角的直線方程. 解: 由交角公式得tan45°=│![]() │從而得k=0, 故所求方程為 y=2
│從而得k=0, 故所求方程為 y=2
( )
設(shè)點 是拋物線
是拋物線

 的焦點,
的焦點, 是拋物線
是拋物線 上的
上的 個不同的點(
個不同的點(
 ).
).
(1) 當 時,試寫出拋物線
時,試寫出拋物線 上的三個定點
上的三個定點 、
、 、
、 的坐標,從而使得
的坐標,從而使得
 ;
;
(2)當 時,若
時,若 ,
,
求證: ;
;
(3) 當 時,某同學對(2)的逆命題,即:
時,某同學對(2)的逆命題,即:
“若 ,則
,則 .”
.”
開展了研究并發(fā)現(xiàn)其為假命題.
請你就此從以下三個研究方向中任選一個開展研究:
① 試構(gòu)造一個說明該逆命題確實是假命題的反例(本研究方向最高得4分);
② 對任意給定的大于3的正整數(shù) ,試構(gòu)造該假命題反例的一般形式,并說明你的理由(本研究方向最高得8分);
,試構(gòu)造該假命題反例的一般形式,并說明你的理由(本研究方向最高得8分);
③ 如果補充一個條件后能使該逆命題為真,請寫出你認為需要補充的一個條件,并說明加上該條件后,能使該逆命題為真命題的理由(本研究方向最高得10分).
【評分說明】本小題若填空不止一個研究方向,則以實得分最高的一個研究方向的得分作為本小題的最終得分.
【解析】第一問利用拋物線 的焦點為
的焦點為 ,設(shè)
,設(shè) ,
,
分別過 作拋物線
作拋物線 的準線
的準線 的垂線,垂足分別為
的垂線,垂足分別為 .
.
由拋物線定義得到
第二問設(shè) ,分別過
,分別過 作拋物線
作拋物線 的準線
的準線 垂線,垂足分別為
垂線,垂足分別為 .
.
由拋物線定義得


第三問中①取 時,拋物線
時,拋物線 的焦點為
的焦點為 ,
,
設(shè) ,
, 分別過
分別過
 作拋物線
作拋物線 的準線
的準線 垂線,垂足分別為
垂線,垂足分別為
 .由拋物線定義得
.由拋物線定義得




 ,
,
則 ,不妨取
,不妨取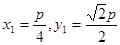 ;
;
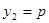 ;
;
 ;
;
解:(1)拋物線 的焦點為
的焦點為 ,設(shè)
,設(shè) ,
,
分別過 作拋物線
作拋物線 的準線
的準線 的垂線,垂足分別為
的垂線,垂足分別為 .由拋物線定義得
.由拋物線定義得


因為 ,所以
,所以 ,
,
故可取

 滿足條件.
滿足條件.
(2)設(shè) ,分別過
,分別過 作拋物線
作拋物線 的準線
的準線 垂線,垂足分別為
垂線,垂足分別為 .
.
由拋物線定義得


 又因為
又因為



 ;
;
所以

 .
.
(3) ①取 時,拋物線
時,拋物線 的焦點為
的焦點為 ,
,
設(shè) ,
, 分別過
分別過
 作拋物線
作拋物線 的準線
的準線 垂線,垂足分別為
垂線,垂足分別為
 .由拋物線定義得
.由拋物線定義得




 ,
,
則 ,不妨取
,不妨取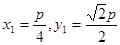 ;
;
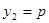 ;
;
 ;
; ,
,
則

 ,
,

 .
.
故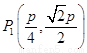 ,
, ,
, ,
, 是一個當
是一個當 時,該逆命題的一個反例.(反例不唯一)
時,該逆命題的一個反例.(反例不唯一)
② 設(shè) ,分別過
,分別過 作
作
拋物線 的準線
的準線 的垂線,垂足分別為
的垂線,垂足分別為 ,
,
由 及拋物線的定義得
及拋物線的定義得
 ,即
,即 .
.
因為上述表達式與點 的縱坐標無關(guān),所以只要將這
的縱坐標無關(guān),所以只要將這 點都取在
點都取在 軸的上方,則它們的縱坐標都大于零,則
軸的上方,則它們的縱坐標都大于零,則






 ,
,
而 ,所以
,所以 .
.
(說明:本質(zhì)上只需構(gòu)造滿足條件且 的一組
的一組 個不同的點,均為反例.)
個不同的點,均為反例.)
③ 補充條件1:“點 的縱坐標
的縱坐標 (
( )滿足
)滿足  ”,即:
”,即:
“當 時,若
時,若 ,且點
,且點 的縱坐標
的縱坐標 (
( )滿足
)滿足 ,則
,則 ”.此命題為真.事實上,設(shè)
”.此命題為真.事實上,設(shè) ,
,
分別過 作拋物線
作拋物線 準線
準線 的垂線,垂足分別為
的垂線,垂足分別為 ,由
,由 ,
,
及拋物線的定義得 ,即
,即 ,則
,則






 ,
,
又由 ,所以
,所以 ,故命題為真.
,故命題為真.
補充條件2:“點 與點
與點
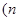 為偶數(shù),
為偶數(shù), 關(guān)于
關(guān)于 軸對稱”,即:
軸對稱”,即:
“當 時,若
時,若 ,且點
,且點 與點
與點
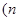 為偶數(shù),
為偶數(shù), 關(guān)于
關(guān)于 軸對稱,則
軸對稱,則 ”.此命題為真.(證略)
”.此命題為真.(證略)
已知等比數(shù)列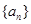 中,
中,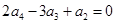 ,且
,且 ,公比
,公比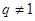 ,(1)求
,(1)求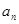 ;(2)設(shè)
;(2)設(shè) ,求數(shù)列
,求數(shù)列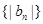 的前
的前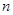 項和
項和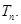
【解析】第一問,因為由題設(shè)可知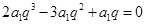
又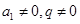 故
故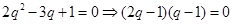
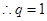 或
或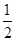 ,又由題設(shè)
,又由題設(shè)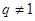
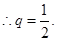 從而
從而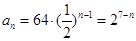
第二問中,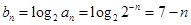
當 時,
時,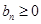 ,
, 時
時
故 時,
時,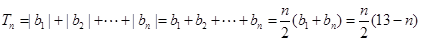
 時,
時,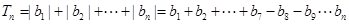
分別討論得到結(jié)論。
由題設(shè)可知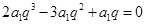
又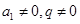 故
故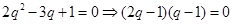
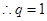 或
或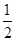 ,又由題設(shè)
,又由題設(shè)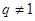
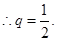
從而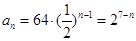 ……………………4分
……………………4分
(2)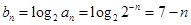
當 時,
時,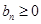 ,
, 時
時 ……………………6分
……………………6分
故 時,
時,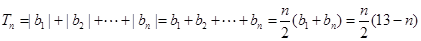 ……8分
……8分
 時,
時,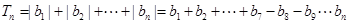
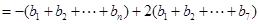
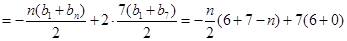
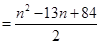 ……………………10分
……………………10分
綜上可得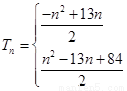

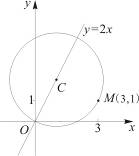
求圓心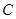 在直線
在直線 上,且經(jīng)過原點及點
上,且經(jīng)過原點及點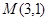 的圓
的圓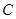 的標準方程.
的標準方程.
【解析】本試題主要考查的圓的方程的求解,利用圓心和半徑表示圓,首先設(shè)圓心C的坐標為( ),然后利用
),然后利用 ,得到
,得到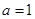 ,從而圓心
,從而圓心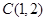 ,半徑
,半徑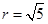 .可得原點 標準方程。
.可得原點 標準方程。
解:設(shè)圓心C的坐標為( ),...........2分
),...........2分
則 ,即
,即
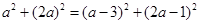 ,解得
,解得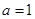 ........4分
........4分
所以圓心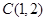 ,半徑
,半徑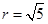 ...........8分
...........8分
故圓C的標準方程為: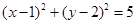 .......10分
.......10分
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com