
題目列表(包括答案和解析)
 ;②a=1;③
;②a=1;③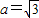 ;建立適當的空間直角坐標系,
;建立適當的空間直角坐標系,
 ;②a=1;③
;②a=1;③ ;建立適當的空間直角坐標系,
;建立適當的空間直角坐標系,
 ;②a=1;③
;②a=1;③ ;建立適當的空間直角坐標系,
;建立適當的空間直角坐標系,
 ;②a=1;③
;②a=1;③ ;建立適當的空間直角坐標系,
;建立適當的空間直角坐標系,
 如圖所示,矩形ABCD的邊AB=a,BC=2,PA⊥平面ABCD,PA=2,現有數據:
如圖所示,矩形ABCD的邊AB=a,BC=2,PA⊥平面ABCD,PA=2,現有數據:
| ||
| 2 |
| 3 |
一.填空題:
1. ; 2.
; 2. ;
3.
;
3. 4.2;
5.
4.2;
5. ;
;
6.  ; 7.
; 7. ; 8.3;
9.
; 8.3;
9. ; 10.
; 10. .
.
二.選擇題:11.B ; 12.C; 13.C.
三.解答題:
14.[解](Ⅰ)方法一(綜合法)設線段 的中點為
的中點為 ,連接
,連接 ,
,
則 為異面直線OC與
為異面直線OC與 所成的角(或其補角) ………………………………..1分
所成的角(或其補角) ………………………………..1分
由已知,可得 ,
,

 為直角三角形 ……………………………………………………………….1分
為直角三角形 ……………………………………………………………….1分
 , ……………………………………………………………….4分
, ……………………………………………………………….4分
 .
.
所以,異面直線OC與MD所成角的大小 . …………………………..1分
. …………………………..1分
方法二(向量法)
以AB,AD,AO所在直線為 軸建立坐標系,
軸建立坐標系,
則 ,
……………………………………………………2分
,
……………………………………………………2分
 ,
, ,
………………………………………………………………………………..1分
,
………………………………………………………………………………..1分
設異面直線OC與MD所成角為 ,
,
 .……………………………….. …………………………2分
.……………………………….. …………………………2分
 OC與MD所成角的大小為
OC與MD所成角的大小為 .…………………………………………………1分
.…………………………………………………1分
(Ⅱ)方法一(綜合法)
作 于
于 , ……………………………………………………………………………1分
, ……………………………………………………………………………1分
 且
且 ,
, 平面
平面

 平面
平面 ………………………………………………………………………………4分
………………………………………………………………………………4分
所以,點 到平面
到平面 的距離
的距離 …………………………………………………2分
…………………………………………………2分
方法二(向量法)
設平面 的一個法向量
的一個法向量 ,
,
 …………………………………………………………………2分
…………………………………………………………………2分
 .
.
 ……………………………………………………………………………………….2分
……………………………………………………………………………………….2分
設 到平面
到平面 的距離為
的距離為
則 .……………………………………………………………………3分
.……………………………………………………………………3分
15.[解](Ⅰ)設“小明中一等獎”為事件 ,“小輝中一等獎”為事件
,“小輝中一等獎”為事件 ,事件
,事件 與事件
與事件 相互獨立,
相互獨立,
 他們倆都中一等獎,則
他們倆都中一等獎,則

所以,購買兩張這種彩票都中一等獎的概率為 . ………………………………..4分
. ………………………………..4分
(Ⅱ)事件 的含義是“買這種彩票中獎”,或“買這種彩票中一等獎或中二等獎”…1分
的含義是“買這種彩票中獎”,或“買這種彩票中一等獎或中二等獎”…1分
顯然,事件A與事件B互斥,
所以, ………………………………..3分
………………………………..3分
故購買一張這種彩票能中獎的概率為 .……………………………………………………..1分
.……………………………………………………..1分
(Ⅲ)對應不中獎、中二等獎、中一等獎, 的分布列如下:
的分布列如下:








…………………………………………..………………………………………………….3分

購買一張這種彩票的期望收益為損失 元.…………………………………………………..3分
元.…………………………………………………..3分
16.[解] (Ⅰ)由于 恒成立,所以函數
恒成立,所以函數 的定義域為
的定義域為 ………………..2分
………………..2分
 ,
,
(1)當 時,函數
時,函數 ,函數
,函數 的值域為
的值域為 …………………………1分
…………………………1分
(2)當 時,因為
時,因為 ,所以
,所以 ,
,
 ,從而
,從而 ,………………………………………………..3分
,………………………………………………..3分
所以函數 的值域為
的值域為 . ……………………………………………………….1分
. ……………………………………………………….1分
(Ⅱ)假設函數 是奇函數,則,對于任意的
是奇函數,則,對于任意的 ,有
,有 成立,
成立,
即
 當
當 時,函數
時,函數 是奇函數. …………………………………………………….2分
是奇函數. …………………………………………………….2分
當 時,函數
時,函數 是偶函數. ………………………………………………..2分
是偶函數. ………………………………………………..2分
當 ,且
,且 時,函數
時,函數 是非奇非偶函數. ………………………………….1分
是非奇非偶函數. ………………………………….1分
 對于任意的
對于任意的 ,且
,且 ,
,


 ………………………………………..3分
………………………………………..3分
所以,當 時,函數
時,函數 是常函數 ………………………………………..1分
是常函數 ………………………………………..1分
 當
當 時,函數
時,函數 是遞減函數. ………………………………………..1分
是遞減函數. ………………………………………..1分
17.[解](Ⅰ)由題意, ……………………………6分
……………………………6分
(Ⅱ)解法1:由 且
且 知
知
 ,
, ,
,
 ,
, ,
,
因此,可猜測 (
( ) ………………………………………………………4分
) ………………………………………………………4分
將 ,
, 代入原式左端得
代入原式左端得
左端


即原式成立,故 為數列的通項.……………………………………………………….3分
為數列的通項.……………………………………………………….3分
用數學歸納法證明得3分
解法2:由  ,
,
令 得
得 ,且
,且
即 ,……… ……………………………………………………………..4分
,……… ……………………………………………………………..4分
所以
因此 ,
, ,...,
,...,
將各式相乘得 ………………………………………………………………………………3分
………………………………………………………………………………3分
(Ⅲ)設上表中每行的公比都為 ,且
,且 .因為
.因為 ,
,
所以表中第1行至第9行共含有數列 的前63項,故
的前63項,故 在表中第10行第三列,………2分
在表中第10行第三列,………2分
因此 .又
.又 ,所以
,所以 . …………………………………..3分
. …………………………………..3分
則 .
. …………………………………………2分
…………………………………………2分
18.[解](Ⅰ)動點 的軌跡是以
的軌跡是以 為原點,以3為半徑的球面 ……………………………1分
為原點,以3為半徑的球面 ……………………………1分
并設動點 的坐標為
的坐標為 ,動點
,動點 滿足
滿足 .
.
則球面的方程為 . …………………………………………………4分
. …………………………………………………4分
(Ⅱ)設動點 ,則
,則
所以 ……………………………………………………………5分
……………………………………………………………5分
整理得曲面 的方程:
的方程: (*) …………………………………………2分
(*) …………………………………………2分
若坐標系原點建在平面 上的點
上的點 處,可得曲面
處,可得曲面 的方程:
的方程: 同樣得分.
同樣得分.
(Ⅲ)(1)對稱性:由于 點關于
點關于 平面的對稱點
平面的對稱點 、關于
、關于 平面的對稱點
平面的對稱點 均滿足方程(*),所以曲面
均滿足方程(*),所以曲面 關于
關于 平面與
平面與 平面對稱. …………………2分
平面對稱. …………………2分
又由于 點關于
點關于 軸的對稱點
軸的對稱點 滿足方程(*),所以曲面
滿足方程(*),所以曲面 關于
關于 軸對稱.
軸對稱.
(2)范圍:由于 ,所以,
,所以, ,即曲面
,即曲面 在
在 平面上方. ………………2分
平面上方. ………………2分
 (3)頂點:令
(3)頂點:令 ,得
,得 ,即坐標原點在曲面
,即坐標原點在曲面 上,
上, 點是曲面
點是曲面 的頂點. …2分
的頂點. …2分
…………………………2分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com