
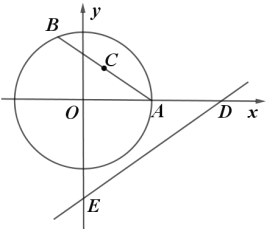
【題目】如圖,在平面直角坐標(biāo)系![]() 中,半徑為2的
中,半徑為2的![]() 與
與![]() 軸的正半軸交于點(diǎn)
軸的正半軸交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 上一動點(diǎn),點(diǎn)
上一動點(diǎn),點(diǎn)![]() 為弦
為弦![]() 的中點(diǎn),直線
的中點(diǎn),直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點(diǎn)
軸分別交于點(diǎn)![]() 、
、![]() ,則
,則![]() 面積的最小值為________.
面積的最小值為________.
【答案】2
【解析】
如圖,連接OB,取OA的中點(diǎn)M,連接CM,過點(diǎn)M作MN⊥DE于N.首先證明點(diǎn)C的運(yùn)動軌跡是以M為圓心,1為半徑的⊙M,設(shè)⊙M交MN于C′.求出MN,當(dāng)點(diǎn)C與C′重合時(shí),△C′DE的面積最小.
解:如圖,連接OB,取OA的中點(diǎn)M,連接CM,過點(diǎn)M作MN⊥DE于N.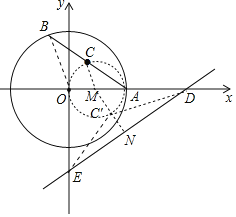
∵AC=CB,AM=OM,
∴MC=![]() OB=1,
OB=1,
∴點(diǎn)C的運(yùn)動軌跡是以M為圓心,1為半徑的⊙M,設(shè)⊙M交MN于C′.
∵直線y=![]() x-3與x軸、y軸分別交于點(diǎn)D、E,
x-3與x軸、y軸分別交于點(diǎn)D、E,
∴D(4,0),E(0,-3),
∴OD=4,OE=3,
∴![]() ,
,
∵∠MDN=∠ODE,∠MND=∠DOE,
∴△DNM∽△DOE,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
當(dāng)點(diǎn)C與C′重合時(shí),△C′DE的面積最小,△C′DE的面積最小值![]() ,
,
故答案為2.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
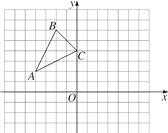
【題目】如圖,已知A(-4,2),B(-2,6),C(0,4)是直角坐標(biāo)系中的三點(diǎn).
(1)把△ABC向右平移4個(gè)單位再向下平移1個(gè)單位,得到△A1B1C1,畫出平移后的圖形,并寫出點(diǎn)A的對應(yīng)點(diǎn)A1的坐標(biāo);
(2)以原點(diǎn)O為位似中心,將△ABC縮小為原來的一半,得到△A2B2C2,請?jiān)谒o的坐標(biāo)系中作出所有滿足條件的圖形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】端午節(jié)是中國的傳統(tǒng)節(jié)日.今年端午節(jié)前夕,遂寧市某食品廠抽樣調(diào)查了河?xùn)|某居民區(qū)市民對A、B、C、D四種不同口味粽子樣品的喜愛情況,并將調(diào)查情況繪制成如圖兩幅不完整統(tǒng)計(jì)圖:
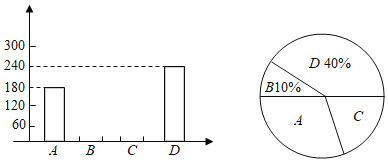
(1)本次參加抽樣調(diào)查的居民有 人.
(2)喜歡C種口味粽子的人數(shù)所占圓心角為 度.根據(jù)題中信息補(bǔ)全條形統(tǒng)計(jì)圖.
(3)若該居民小區(qū)有6000人,請你估計(jì)愛吃D種粽子的有 人.
(4)若有外型完全相同的A、B、C、D棕子各一個(gè),煮熟后,小李吃了兩個(gè),請用列表或畫樹狀圖的方法求他第二個(gè)吃的粽子恰好是A種粽子的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
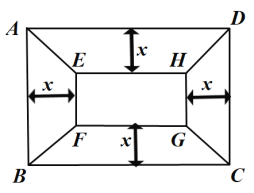
【題目】有一塊矩形地塊![]() ,
,![]() 米,
米,![]() 米,為美觀,擬種植不同的花卉,如圖所示,將矩形
米,為美觀,擬種植不同的花卉,如圖所示,將矩形![]() 分割成四個(gè)等腰梯形及一個(gè)矩形,其中梯形的高相等,均為
分割成四個(gè)等腰梯形及一個(gè)矩形,其中梯形的高相等,均為![]() 米.現(xiàn)決定在等腰梯形
米.現(xiàn)決定在等腰梯形![]() 和
和![]() 中種植甲種花卉;在等腰梯形
中種植甲種花卉;在等腰梯形![]() 和
和![]() 中種植乙種花卉;在矩形
中種植乙種花卉;在矩形![]() 中種植丙種花卉.甲、乙、丙三種花卉的種植成本分別為20元/米
中種植丙種花卉.甲、乙、丙三種花卉的種植成本分別為20元/米![]() 、60 元/米
、60 元/米![]() 、40元/米
、40元/米![]() ,設(shè)三種花卉的種植總成本為
,設(shè)三種花卉的種植總成本為![]() 元.
元.
(1)當(dāng)![]() 時(shí),求種植總成本
時(shí),求種植總成本![]() ;
;
(2)求種植總成本![]() 與
與![]() 的函數(shù)表達(dá)式,并寫出自變量
的函數(shù)表達(dá)式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(3)若甲、乙兩種花卉的種植面積之差不超過120米![]() ,求三種花卉的最低種植總成本.
,求三種花卉的最低種植總成本.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,P是對角線BD上的一點(diǎn),過點(diǎn)C作CQ∥DB,且CQ=DP,連接AP、BQ、PQ.
(1)求證:△APD≌△BQC;
(2)若∠ABP+∠BQC=180°,求證:四邊形ABQP為菱形.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
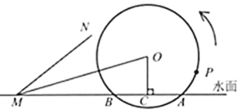
【題目】筒車是我國古代利用水力驅(qū)動的灌溉工具,唐代陳廷章在《水輪賦》中寫道:“水能利物,輪乃曲成”.如圖,半徑為![]() 的筒車
的筒車![]() 按逆時(shí)針方向每分鐘轉(zhuǎn)
按逆時(shí)針方向每分鐘轉(zhuǎn)![]() 圈,筒車與水面分別交于點(diǎn)
圈,筒車與水面分別交于點(diǎn)![]() 、
、![]() ,筒車的軸心
,筒車的軸心![]() 距離水面的高度
距離水面的高度![]() 長為
長為![]() ,簡車上均勻分布著若干個(gè)盛水筒.若以某個(gè)盛水筒
,簡車上均勻分布著若干個(gè)盛水筒.若以某個(gè)盛水筒![]() 剛浮出水面時(shí)開始計(jì)算時(shí)間.
剛浮出水面時(shí)開始計(jì)算時(shí)間.

(1)經(jīng)過多長時(shí)間,盛水筒![]() 首次到達(dá)最高點(diǎn)?
首次到達(dá)最高點(diǎn)?
(2)浮出水面3.4秒后,盛水筒![]() 距離水面多高?
距離水面多高?
(3)若接水槽![]() 所在直線是
所在直線是![]() 的切線,且與直線
的切線,且與直線![]() 交于點(diǎn)
交于點(diǎn)![]() ,
,![]() .求盛水筒
.求盛水筒![]() 從最高點(diǎn)開始,至少經(jīng)過多長時(shí)間恰好在直線
從最高點(diǎn)開始,至少經(jīng)過多長時(shí)間恰好在直線![]() 上.(參考數(shù)據(jù):
上.(參考數(shù)據(jù):![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖是某小型汽車的側(cè)面示意圖,其中矩形ABCD表示該車的后備箱,在打開后備箱的過程中,箱蓋ADE可以繞點(diǎn)A逆時(shí)針方向旋轉(zhuǎn),當(dāng)旋轉(zhuǎn)角是50度時(shí),箱蓋落在![]() 的位置(如圖2),已知
的位置(如圖2),已知![]()
![]()
![]()
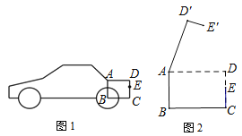
(1)求點(diǎn)![]() 到
到![]() 的距離;(結(jié)果保留整數(shù))
的距離;(結(jié)果保留整數(shù))
(2)求![]() 兩點(diǎn)之間的距離.(結(jié)果保留整數(shù))
兩點(diǎn)之間的距離.(結(jié)果保留整數(shù))
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀材料解答下列問題
觀察下列方程:①![]() ,②
,②![]() ,③
,③![]() ……
……
⑴按此規(guī)律寫出關(guān)于x的第n個(gè)方程為____________________,此方程的解為____________.
⑵根據(jù)上述結(jié)論,求出![]() 的解.
的解.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一勘測人員從山腳![]() 點(diǎn)出發(fā),沿坡度為
點(diǎn)出發(fā),沿坡度為![]() 的坡面
的坡面![]() 行至
行至![]() 點(diǎn)處時(shí),他的垂直高度上升了
點(diǎn)處時(shí),他的垂直高度上升了![]() 米;然后再從
米;然后再從![]() 點(diǎn)處沿坡角為
點(diǎn)處沿坡角為![]() 的坡面
的坡面![]() 以
以![]() 米/分鐘的速度到達(dá)山頂
米/分鐘的速度到達(dá)山頂![]() 點(diǎn)時(shí),用了
點(diǎn)時(shí),用了![]() 分鐘.
分鐘.
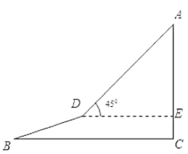
(1)求![]() 點(diǎn)到
點(diǎn)到![]() 點(diǎn)之間的水平距離;
點(diǎn)之間的水平距離;
(2)求山頂![]() 點(diǎn)處的垂直高度
點(diǎn)處的垂直高度![]() 是多少米?(
是多少米?(![]() 結(jié)果保留整數(shù))
結(jié)果保留整數(shù))
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com