
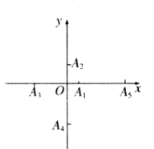
【題目】如圖,在直角坐標系的坐標軸上按如下規律取點:![]() 在
在![]() 軸正半軸上,
軸正半軸上,![]() 在
在![]() 軸正半軸上,
軸正半軸上,![]() 在
在![]() 軸負半軸上,
軸負半軸上,![]() 在
在![]() 軸負半軸上,
軸負半軸上,![]() 在
在![]() 軸正半軸上,......,且
軸正半軸上,......,且![]()
![]() ......,設
......,設![]() ......,有坐標分別為
......,有坐標分別為![]() ,
,![]() ......,
......,![]() .
.
(1)當![]() 時,求
時,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)當![]() 時,直接寫出用含
時,直接寫出用含![]() 為正整數)的式子表示
為正整數)的式子表示![]() 軸負半軸上所取點.
軸負半軸上所取點.
 導學全程練創優訓練系列答案
導學全程練創優訓練系列答案科目:初中數學 來源: 題型:
【題目】閱讀理解:如圖1,在△ABC中,當DE∥BC時可以得到三組成比例線段:① ![]() ;②
;② ![]() ;③
;③ ![]() .反之,當對應線段程比例時也可以推出DE∥BC.
.反之,當對應線段程比例時也可以推出DE∥BC.
理解運用:三角形的內接四邊形是指頂點在三角形各邊上的四邊形.
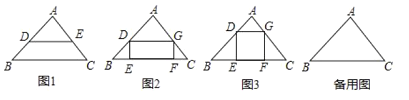
(1)如圖2,已知矩形DEFG是△ABC的一個內接矩形,將矩形DEFG沿CB方向向左平移得矩形PBQH,其中頂點D、E、F、G的對應點分別為P、B、Q、H,在圖2中畫出平移后的圖形;
(2)在(1)所得的圖形中,連接CH并延長交BP的延長線于點R,連接AR.求證:AR∥BC;
(3)如圖3,某小區有一塊三角形空地,已知△ABC空地的邊AB=400米,BC=600米,∠ABC=45°;準備在△ABC內建一個內接矩形廣場DEFG(點E、F在邊BC上,點D、G分別在邊AB和AC上),三角形其余部分進行植被綠化,按要求欲使矩形DEFG的對角線EG最短,請在備用圖中畫出使對角線EG最短的矩形.并求出對角線EG的最短距離(不要求證明).
查看答案和解析>>
科目:初中數學 來源: 題型:
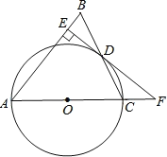
【題目】如圖,在△ABC中,AB=AC,以AC邊為直徑作![]() O交BC邊于點D,過點D作DE⊥AB于點E,ED、AC的延長線交于點F.
O交BC邊于點D,過點D作DE⊥AB于點E,ED、AC的延長線交于點F.
(1)求證:EF是![]() O的切線;
O的切線;
(2)若EB=6,且sin∠CFD=![]() ,求
,求![]() O的半徑.
O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,直線y=x+4與拋物線y=﹣![]() x2+bx+c(b,c是常數)交于A、B兩點,點A在x軸上,點B在y軸上.設拋物線與x軸的另一個交點為點C.
x2+bx+c(b,c是常數)交于A、B兩點,點A在x軸上,點B在y軸上.設拋物線與x軸的另一個交點為點C.

(1)求該拋物線的解析式;
(2)P是拋物線上一動點(不與點A、B重合),
①如圖2,若點P在直線AB上方,連接OP交AB于點D,求![]() 的最大值;
的最大值;
②如圖3,若點P在x軸的上方,連接PC,以PC為邊作正方形CPEF,隨著點P的運動,正方形的大小、位置也隨之改變.當頂點E或F恰好落在y軸上,直接寫出對應的點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與x軸交于點
與x軸交于點![]() ,點
,點![]() ,與y軸交于點C,且過點
,與y軸交于點C,且過點![]() .點P、Q是拋物線
.點P、Q是拋物線![]() 上的動點.
上的動點.
(1)求拋物線的解析式;
(2)當點P在直線OD下方時,求![]() 面積的最大值.
面積的最大值.
(3)直線OQ與線段BC相交于點E,當![]() 與
與![]() 相似時,求點Q的坐標.
相似時,求點Q的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明投資銷售一種進價為每件20元的護眼臺燈.銷售過程中發現,每月銷售量y(件)與銷售單價x(元)之間的關系可近似的看作一次函數:y=﹣10x+500,在銷售過程中銷售單價不低于成本價,而每件的利潤不高于成本價的60%.
(1)設小明每月獲得利潤為w(元),求每月獲得利潤w(元)與銷售單價x(元)之間的函數關系式,并確定自變量x的取值范圍.
(2)當銷售單價定為多少元時,每月可獲得最大利潤?每月的最大利潤是多少?
(3)如果小明想要每月獲得的利潤不低于2000元,那么小明每月的成本最少需要多少元?(成本=進價×銷售量)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com