
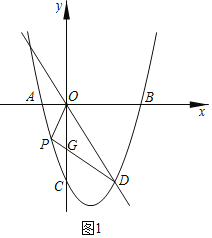
【題目】如圖,拋物線![]() 與x軸交于點(diǎn)
與x軸交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,與y軸交于點(diǎn)C,且過(guò)點(diǎn)
,與y軸交于點(diǎn)C,且過(guò)點(diǎn)![]() .點(diǎn)P、Q是拋物線
.點(diǎn)P、Q是拋物線![]() 上的動(dòng)點(diǎn).
上的動(dòng)點(diǎn).
(1)求拋物線的解析式;
(2)當(dāng)點(diǎn)P在直線OD下方時(shí),求![]() 面積的最大值.
面積的最大值.
(3)直線OQ與線段BC相交于點(diǎn)E,當(dāng)![]() 與
與![]() 相似時(shí),求點(diǎn)Q的坐標(biāo).
相似時(shí),求點(diǎn)Q的坐標(biāo).

【答案】(1)拋物線的表達(dá)式為:![]() ;(2)
;(2)![]() 有最大值,當(dāng)
有最大值,當(dāng)![]() 時(shí),其最大值為
時(shí),其最大值為![]() ;(3)
;(3) ![]() 或
或![]() 或
或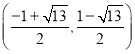 或
或 .
.
【解析】
(1)函數(shù)的表達(dá)式為:y=a(x+1)(x-3),將點(diǎn)D坐標(biāo)代入上式,即可求解;
(2)設(shè)點(diǎn)![]() ,求出
,求出![]() ,根據(jù)
,根據(jù)![]()
![]()
![]() ,利用二次函數(shù)的性質(zhì)即可求解;
,利用二次函數(shù)的性質(zhì)即可求解;
(3)分∠ACB=∠BOQ、∠BAC=∠BOQ,兩種情況分別求解,通過(guò)角的關(guān)系,確定直線OQ傾斜角,進(jìn)而求解.
解:(1)函數(shù)的表達(dá)式為:![]() ,將點(diǎn)D坐標(biāo)代入上式并解得:
,將點(diǎn)D坐標(biāo)代入上式并解得:![]() ,
,
故拋物線的表達(dá)式為:![]() …①;
…①;
(2)設(shè)直線PD與y軸交于點(diǎn)G,設(shè)點(diǎn)![]() ,
,
將點(diǎn)P、D的坐標(biāo)代入一次函數(shù)表達(dá)式:![]() 并解得,直線PD的表達(dá)式為:
并解得,直線PD的表達(dá)式為:![]() ,則
,則![]() ,
,
![]()
![]()
![]() ,
,
∵![]() ,故
,故![]() 有最大值,當(dāng)
有最大值,當(dāng)![]() 時(shí),其最大值為
時(shí),其最大值為![]() ;
;
(3)∵![]() ,∴
,∴![]() ,
,
∵![]() ,故
,故![]() 與
與![]() 相似時(shí),分為兩種情況:
相似時(shí),分為兩種情況:
①當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() ,
,![]() ,
,
過(guò)點(diǎn)A作AH⊥BC與點(diǎn)H,

![]() ,解得:
,解得:![]() ,
,
∴CH=![]()
則![]() ,
,
則直線OQ的表達(dá)式為:![]() …②,
…②,
聯(lián)立①②并解得:![]() ,
,
故點(diǎn)![]() 或
或![]() ;
;
②![]() 時(shí),
時(shí),
![]() ,
,
則直線OQ的表達(dá)式為:![]() …③,
…③,
聯(lián)立①③并解得:![]() ,
,
故點(diǎn)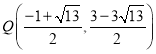 或
或 ;
;
綜上,點(diǎn)![]() 或
或![]() 或
或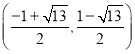 或
或 .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示是我國(guó)古代城市用以滯洪或分洪系統(tǒng)的局部截面原理圖,圖中![]() 為下水管道口直徑,
為下水管道口直徑,![]() 為可繞轉(zhuǎn)軸
為可繞轉(zhuǎn)軸![]() 自由轉(zhuǎn)動(dòng)的閥門,平時(shí)閥門被管道中排出的水沖開(kāi),可排出城市污水:當(dāng)河水上漲時(shí),閥門會(huì)因河水壓迫而關(guān)閉,以防止河水倒灌入城中.若閥門的直徑
自由轉(zhuǎn)動(dòng)的閥門,平時(shí)閥門被管道中排出的水沖開(kāi),可排出城市污水:當(dāng)河水上漲時(shí),閥門會(huì)因河水壓迫而關(guān)閉,以防止河水倒灌入城中.若閥門的直徑![]() ,
,![]() 為檢修時(shí)閥門開(kāi)啟的位置,且
為檢修時(shí)閥門開(kāi)啟的位置,且![]() .
.
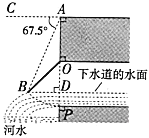
(1)直接寫(xiě)出閥門被下水道的水沖開(kāi)與被河水關(guān)閉過(guò)程中![]() 的取值范圍;
的取值范圍;
(2)為了觀測(cè)水位,當(dāng)下水道的水沖開(kāi)閥門到達(dá)![]() 位置時(shí),在點(diǎn)
位置時(shí),在點(diǎn)![]() 處測(cè)得俯角
處測(cè)得俯角![]() ,若此時(shí)點(diǎn)
,若此時(shí)點(diǎn)![]() 恰好與下水道的水平面齊平,求此時(shí)下水道內(nèi)水的深度.(結(jié)果保留根號(hào))
恰好與下水道的水平面齊平,求此時(shí)下水道內(nèi)水的深度.(結(jié)果保留根號(hào))
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】下面是小東設(shè)計(jì)的“過(guò)直線上一點(diǎn)作這條直線的垂線”的尺規(guī)作圖過(guò)程.
已知:直線l及直線l上一點(diǎn)P.
![]()
求作:直線PQ,使得PQ⊥l.
作法:如圖,
![]()
①在直線l上取一點(diǎn)A(不與點(diǎn)P重合),分別以點(diǎn)P,A為圓心,AP長(zhǎng)為半徑畫(huà)弧,兩弧在直線l的上方相交于點(diǎn)B;
②作射線AB,以點(diǎn)B為圓心,AP長(zhǎng)為半徑畫(huà)弧,交AB的延長(zhǎng)線于點(diǎn)Q;
③作直線PQ.
所以直線PQ就是所求作的直線.
根據(jù)小東設(shè)計(jì)的尺規(guī)作圖過(guò)程,
(1)使用直尺和圓規(guī),補(bǔ)全圖形;(保留作圖痕跡)
(2)完成下面的證明.
證明:連接BP,
∵ = = =AP,
∴點(diǎn)A,P,Q在以點(diǎn)B為圓心,AP長(zhǎng)為半徑的圓上.
∴∠APQ=90°( ).(填寫(xiě)推理的依據(jù))
即PQ⊥l.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在直角坐標(biāo)系的坐標(biāo)軸上按如下規(guī)律取點(diǎn):![]() 在
在![]() 軸正半軸上,
軸正半軸上,![]() 在
在![]() 軸正半軸上,
軸正半軸上,![]() 在
在![]() 軸負(fù)半軸上,
軸負(fù)半軸上,![]() 在
在![]() 軸負(fù)半軸上,
軸負(fù)半軸上,![]() 在
在![]() 軸正半軸上,......,且
軸正半軸上,......,且![]()
![]() ......,設(shè)
......,設(shè)![]() ......,有坐標(biāo)分別為
......,有坐標(biāo)分別為![]() ,
,![]() ......,
......,![]() .
.
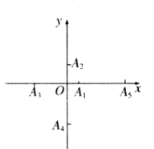
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)當(dāng)![]() 時(shí),直接寫(xiě)出用含
時(shí),直接寫(xiě)出用含![]() 為正整數(shù))的式子表示
為正整數(shù))的式子表示![]() 軸負(fù)半軸上所取點(diǎn).
軸負(fù)半軸上所取點(diǎn).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知半圓O的直徑AB=4,沿它的一條弦折疊.若折疊后的圓弧與直徑AB相切于點(diǎn)D,且AD:DB=3:1,則折痕EF的長(zhǎng)______.
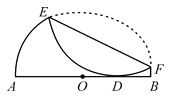
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】2019年4月15日傍晚法國(guó)地標(biāo)性建筑巴黎圣母院突遭大火吞噬,導(dǎo)致屋頂和主尖塔坍塌,哥特式的玫瑰花窗損毀.為了重建巴黎圣母院,設(shè)計(jì)小組設(shè)計(jì)了一個(gè)由三色玻璃拼成的花窗,如圖所示,主體部分由矩形![]() 和半圓
和半圓![]() 組成,設(shè)半圓
組成,設(shè)半圓![]() 為區(qū)域
為區(qū)域![]() ,四個(gè)全等的直角三角形
,四個(gè)全等的直角三角形![]() 為區(qū)域
為區(qū)域![]() ,矩形內(nèi)的陰影部分為區(qū)域
,矩形內(nèi)的陰影部分為區(qū)域![]() ,其中
,其中![]() ,設(shè)
,設(shè)![]()
![]() 當(dāng)
當(dāng)![]() ,求區(qū)域
,求區(qū)域![]() 的面積.
的面積.
![]() 請(qǐng)用
請(qǐng)用![]() 的代數(shù)式表示出區(qū)域
的代數(shù)式表示出區(qū)域![]() 的面積并求出其最大值.
的面積并求出其最大值.
![]() 為了美觀,設(shè)置區(qū)域
為了美觀,設(shè)置區(qū)域![]() 與區(qū)域
與區(qū)域![]() 的面積之比為
的面積之比為![]() .區(qū)域
.區(qū)域![]() 、區(qū)域
、區(qū)域![]() 、區(qū)域
、區(qū)域![]() 分別鑲嵌紅、藍(lán)、黃色三種玻璃,已知這三種玻璃的單價(jià)之和為
分別鑲嵌紅、藍(lán)、黃色三種玻璃,已知這三種玻璃的單價(jià)之和為![]() 元(三種玻璃的單價(jià)均為整數(shù)),整個(gè)花窗鑲嵌玻璃共花費(fèi)了
元(三種玻璃的單價(jià)均為整數(shù)),整個(gè)花窗鑲嵌玻璃共花費(fèi)了![]() 元,求這三種玻璃的單價(jià).(
元,求這三種玻璃的單價(jià).(![]() 取
取![]() )
)

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:如圖,在△ABC中,BC=AC,以BC為直徑的⊙O與邊AB相交于點(diǎn)D,DE⊥AC,垂足為點(diǎn)E.
(1)求證:點(diǎn)D是AB的中點(diǎn);
(2)判斷DE與⊙O的位置關(guān)系,并證明你的結(jié)論;
(3)若⊙O的直徑為10,tanB=3,求DE的長(zhǎng).
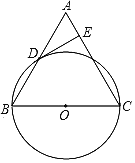
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,拋物線y=x2﹣2mx+m2﹣1與y軸交于點(diǎn)C.
(1)試用含m的代數(shù)式表示拋物線的頂點(diǎn)坐標(biāo);
(2)將拋物線y=x2﹣2mx+m2﹣1沿直線y=﹣1翻折,得到的新拋物線與y軸交于點(diǎn)D,若m>0,CD=8,求m的值.
(3)已知A(﹣k+4,1),B(1,k﹣2),在(2)的條件下,當(dāng)線段AB與拋物線y=x2﹣2mx+m2﹣1只有一個(gè)公共點(diǎn)時(shí),請(qǐng)求出k的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
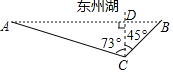
【題目】某市為了創(chuàng)建綠色生態(tài)城市,在城東建了“東州湖”景區(qū),小明和小亮想測(cè)量“東州湖”東西兩端A、B間的距離.于是,他們?nèi)チ撕叄鐖D,在湖的南岸的水平地面上,選取了可直接到達(dá)點(diǎn)B的一點(diǎn)C,并測(cè)得BC=350米,點(diǎn)A位于點(diǎn)C的北偏西73°方向,點(diǎn)B位于點(diǎn)C的北偏東45°方向.請(qǐng)你根據(jù)以上提供的信息,計(jì)算“東州湖”東西兩端之間AB的長(zhǎng).(結(jié)果精確到1米)(參考數(shù)據(jù):sin73°≈0.9563,cos73≈0.2924,tan73°≈3.2709,![]() ≈1.414.)
≈1.414.)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com