
【題目】如圖所示是我國古代城市用以滯洪或分洪系統的局部截面原理圖,圖中![]() 為下水管道口直徑,
為下水管道口直徑,![]() 為可繞轉軸
為可繞轉軸![]() 自由轉動的閥門,平時閥門被管道中排出的水沖開,可排出城市污水:當河水上漲時,閥門會因河水壓迫而關閉,以防止河水倒灌入城中.若閥門的直徑
自由轉動的閥門,平時閥門被管道中排出的水沖開,可排出城市污水:當河水上漲時,閥門會因河水壓迫而關閉,以防止河水倒灌入城中.若閥門的直徑![]() ,
,![]() 為檢修時閥門開啟的位置,且
為檢修時閥門開啟的位置,且![]() .
.
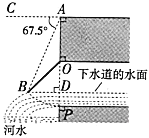
(1)直接寫出閥門被下水道的水沖開與被河水關閉過程中![]() 的取值范圍;
的取值范圍;
(2)為了觀測水位,當下水道的水沖開閥門到達![]() 位置時,在點
位置時,在點![]() 處測得俯角
處測得俯角![]() ,若此時點
,若此時點![]() 恰好與下水道的水平面齊平,求此時下水道內水的深度.(結果保留根號)
恰好與下水道的水平面齊平,求此時下水道內水的深度.(結果保留根號)
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+c(a≠0)上部分點的橫坐標x與縱坐標y的對應值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求該拋物線的表達式;
(2)已知點E(4, y)是該拋物線上的點,點E關于拋物線的對稱軸對稱的點為點F,求點E和點F的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:如圖1,在△ABC中,當DE∥BC時可以得到三組成比例線段:① ![]() ;②
;② ![]() ;③
;③ ![]() .反之,當對應線段程比例時也可以推出DE∥BC.
.反之,當對應線段程比例時也可以推出DE∥BC.
理解運用:三角形的內接四邊形是指頂點在三角形各邊上的四邊形.
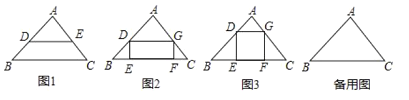
(1)如圖2,已知矩形DEFG是△ABC的一個內接矩形,將矩形DEFG沿CB方向向左平移得矩形PBQH,其中頂點D、E、F、G的對應點分別為P、B、Q、H,在圖2中畫出平移后的圖形;
(2)在(1)所得的圖形中,連接CH并延長交BP的延長線于點R,連接AR.求證:AR∥BC;
(3)如圖3,某小區有一塊三角形空地,已知△ABC空地的邊AB=400米,BC=600米,∠ABC=45°;準備在△ABC內建一個內接矩形廣場DEFG(點E、F在邊BC上,點D、G分別在邊AB和AC上),三角形其余部分進行植被綠化,按要求欲使矩形DEFG的對角線EG最短,請在備用圖中畫出使對角線EG最短的矩形.并求出對角線EG的最短距離(不要求證明).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知銳角∠AOB如圖,(1)在射線OA上取一點C,以點O為圓心,OC長為半徑作![]() ,交射線OB于點D,連接CD;
,交射線OB于點D,連接CD;
(2)分別以點C,D為圓心,CD長為半徑作弧,交![]() 于點M,N;
于點M,N;
(3)連接OM,MN.
根據以上作圖過程及所作圖形,下列結論中錯誤的是( )

A. ∠COM=∠CODB. 若OM=MN,則∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為2,P為CD的中點,連結AP,過點B作BE⊥AP于點E,延長CE交AD于點F,過點C作CH⊥BE于點G,交AB于點H,連接HF.下列結論正確的是( )

A. CE=![]() B. EF=
B. EF=![]() C. cos∠CEP=
C. cos∠CEP=![]() D. HF2=EFCF
D. HF2=EFCF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知邊長為4的正方形鋼板有一個角銹蝕,其中AF=2,BF=1,為了合理利用這塊鋼板.將在五邊形EABCD內截取一個矩形塊MDNP,使點P在AB上,且要求面積最大,求鋼板的最大利用率.
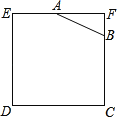
查看答案和解析>>
科目:初中數學 來源: 題型:
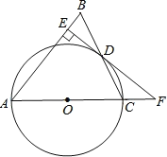
【題目】如圖,在△ABC中,AB=AC,以AC邊為直徑作![]() O交BC邊于點D,過點D作DE⊥AB于點E,ED、AC的延長線交于點F.
O交BC邊于點D,過點D作DE⊥AB于點E,ED、AC的延長線交于點F.
(1)求證:EF是![]() O的切線;
O的切線;
(2)若EB=6,且sin∠CFD=![]() ,求
,求![]() O的半徑.
O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與x軸交于點
與x軸交于點![]() ,點
,點![]() ,與y軸交于點C,且過點
,與y軸交于點C,且過點![]() .點P、Q是拋物線
.點P、Q是拋物線![]() 上的動點.
上的動點.
(1)求拋物線的解析式;
(2)當點P在直線OD下方時,求![]() 面積的最大值.
面積的最大值.
(3)直線OQ與線段BC相交于點E,當![]() 與
與![]() 相似時,求點Q的坐標.
相似時,求點Q的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com