
【題目】如圖,直線y=kx+2與x軸交于點A(3,0),與y軸交于點B,拋物線y=﹣![]() x2+bx+c經(jīng)過點A,B.
x2+bx+c經(jīng)過點A,B.
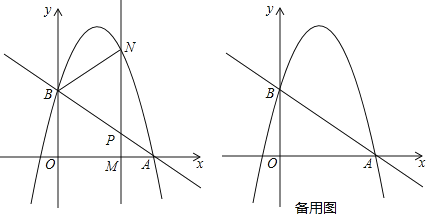
(1)求k的值和拋物線的解析式.
(2)M(m,0)為x軸上一動點,過點M且垂直于x軸的直線與直線AB及拋物線分別交于點P,N,連接BN.
①若△BPN是直角三角形,求點N的坐標(biāo).
②當(dāng)∠PBN=45°時,請直接寫出m的值.(注:當(dāng)k1k2=﹣1時,直線y=k1x+b1與直線y=k2x+b2垂直)
【答案】(1)k=﹣![]() , y=﹣
, y=﹣![]() x2+
x2+![]() x+2;(2)①點N(
x+2;(2)①點N(![]() ,
,![]() );②m=
);②m=![]() 或m=
或m=![]()
【解析】
(1)把![]() 點坐標(biāo)代入直線解析式可求得
點坐標(biāo)代入直線解析式可求得![]() ,則可求得
,則可求得![]() 點坐標(biāo),由
點坐標(biāo),由![]() 、
、![]() 的坐標(biāo),利用待定系數(shù)法可求得拋物線解析式;
的坐標(biāo),利用待定系數(shù)法可求得拋物線解析式;
(2)①分![]() 和
和![]() 兩種情況討論,即可求解;
兩種情況討論,即可求解;
②有兩解,![]() 點在
點在![]() 的上方或下方,作輔助線,構(gòu)建等腰直角三角形,由
的上方或下方,作輔助線,構(gòu)建等腰直角三角形,由![]() 得
得![]() ,設(shè)
,設(shè)![]() ,則由
,則由![]() ,得
,得![]() ,
,![]() ,根據(jù)
,根據(jù)![]() ,可得
,可得![]() 和
和![]() 的解析式,分別與拋物線聯(lián)立方程組,可得結(jié)論.
的解析式,分別與拋物線聯(lián)立方程組,可得結(jié)論.
解:(1)把![]() 代入
代入![]() 中得,
中得,![]() ,
,
![]() ,
,
![]() 直線
直線![]() 的解析式為:
的解析式為:![]() ,
,
![]() ,
,
把![]() 和
和![]() 代入拋物線
代入拋物線![]() 中,
中,
則![]() ,
,
解得: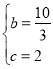 ,
,
二次函數(shù)的表達(dá)式為:![]() ;
;
(2)①當(dāng)![]() 時,且
時,且![]() ,
,
![]() ,
,
![]() ,
,
![]() 點
點![]() 的縱坐標(biāo)為2,
的縱坐標(biāo)為2,
![]() ,
,
![]() (舍去),
(舍去),![]() ,
,
![]() 點
點![]() 坐標(biāo)
坐標(biāo)![]() ,
,![]() ;
;
當(dāng)![]() 時,
時,
直線![]() 的解析式為:
的解析式為:![]() ,
,
![]()
![]() ,
,
![]() (舍去),
(舍去),![]() ,
,
![]() 點N(
點N(![]() ,
,![]() );
);
②有兩解,![]() 點在
點在![]() 的上方或下方,
的上方或下方,
如圖2,過點![]() 作
作![]() 的垂線交
的垂線交![]() 軸于點
軸于點![]() ,
,
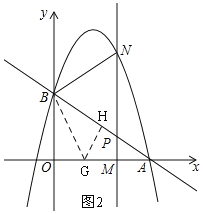
過點![]() 作
作![]() 的垂線,垂足為點
的垂線,垂足為點![]() .
.
由![]() 得
得![]() ,
,
![]() ,
,
設(shè)![]() ,則由
,則由![]() ,
,
![]()
![]() ,
,
得![]() ,
,![]() ,
,
由![]() ,解得
,解得![]() ,
,
![]() ,
,
從而![]() ,
,
即![]() ,
,![]() ,
,
由![]() ,
,![]() ,
,![]() 得:
得:
直線![]() ,直線
,直線![]() .
.
則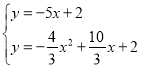 ,
,
解得:![]() (舍),
(舍),![]() ,
,
即![]() ;
;
則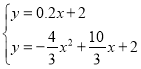 ,
,
解得:![]() (舍
(舍![]() ,
,![]() ;
;
即![]() ;
;
故![]() 與
與![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列命題中,是真命題的是( )
A.將函數(shù)y=![]() x+1向右平移2個單位后所得函數(shù)的解析式為y=
x+1向右平移2個單位后所得函數(shù)的解析式為y=![]() x
x
B.若一個數(shù)的平方根等于其本身,則這個數(shù)是0和1
C.對函數(shù)y=![]() ,其函數(shù)值y隨自變量x的增大而增大
,其函數(shù)值y隨自變量x的增大而增大
D.直線y=3x+1與直線y=﹣3x+2一定互相平行
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,![]() 的三個頂點坐標(biāo)分別為
的三個頂點坐標(biāo)分別為![]() 、
、![]() 、
、![]() .
.
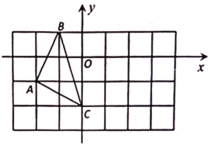
(1)點![]() 關(guān)于坐標(biāo)原點
關(guān)于坐標(biāo)原點![]() 對稱的點的坐標(biāo)為______;
對稱的點的坐標(biāo)為______;
(2)將![]() 繞著點
繞著點![]() 順時針旋轉(zhuǎn)
順時針旋轉(zhuǎn)![]() ,畫出旋轉(zhuǎn)后得到的
,畫出旋轉(zhuǎn)后得到的![]() ;
;
(3)在(2)中,求邊![]() 所掃過區(qū)域的面積是多少?(結(jié)果保留
所掃過區(qū)域的面積是多少?(結(jié)果保留![]() ).
).
(4)若![]() 、
、![]() 、
、![]() 三點的橫坐標(biāo)都加3,縱坐標(biāo)不變,圖形
三點的橫坐標(biāo)都加3,縱坐標(biāo)不變,圖形![]() 的位置發(fā)生怎樣的變化?
的位置發(fā)生怎樣的變化?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知一個二次函數(shù)圖象的頂點是![]() ,且與
,且與![]() 軸的交點的縱坐標(biāo)為4.
軸的交點的縱坐標(biāo)為4.
(1)求這個二次函數(shù)的表達(dá)式;
(2)當(dāng)![]() 取哪些值時,
取哪些值時,![]() 的值隨
的值隨![]() 值的增大而增大?
值的增大而增大?
(3)點![]() 在這個二次函數(shù)的圖象上嗎?
在這個二次函數(shù)的圖象上嗎?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
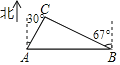
【題目】如圖,從A城市到B城市要翻過一座大山,現(xiàn)需要打通隧道,修建高鐵方便兩地出行,已知在A城市的北偏東30°方向和B城市的北偏西67°方向有一C地,A,C相距230km,求A,B兩個城市之間的距離.(參考數(shù)據(jù):sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.7,結(jié)果精確到1km)
≈1.7,結(jié)果精確到1km)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】一輛慢車與一輛快車分別從甲、乙兩地同時出發(fā),勻速相向而行,兩車相遇后都停下來休息,快車休息2個小時后,以原速的![]() 繼續(xù)向甲行駛,慢車休息3小時后,接到緊急任務(wù),以原速的
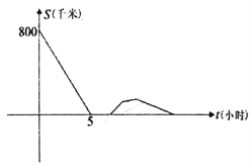
繼續(xù)向甲行駛,慢車休息3小時后,接到緊急任務(wù),以原速的![]() 返回甲地,結(jié)果快車比慢車早2.25小時到達(dá)甲地,兩車之間的距離S(千米)與慢車出發(fā)的時間t(小時)的函數(shù)圖象如圖所示,則當(dāng)快車到達(dá)甲地時,慢車距乙地______千米.
返回甲地,結(jié)果快車比慢車早2.25小時到達(dá)甲地,兩車之間的距離S(千米)與慢車出發(fā)的時間t(小時)的函數(shù)圖象如圖所示,則當(dāng)快車到達(dá)甲地時,慢車距乙地______千米.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】拋物線![]() 經(jīng)過點(1,0),且對稱軸為直線
經(jīng)過點(1,0),且對稱軸為直線![]() ,其部分圖象如圖所示.對于此拋物線有如下四個結(jié)論:①
,其部分圖象如圖所示.對于此拋物線有如下四個結(jié)論:①![]() <0; ②
<0; ②![]() ;③9a-3b+c=0;④若
;③9a-3b+c=0;④若![]() ,則
,則![]() 時的函數(shù)值小于
時的函數(shù)值小于![]() 時的函數(shù)值.其中正確結(jié)論的序號是( )
時的函數(shù)值.其中正確結(jié)論的序號是( )
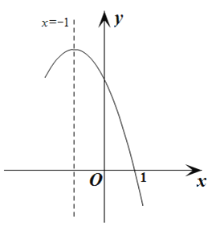
A.①③B.②④C.②③D.③④
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
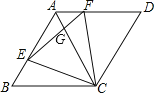
【題目】如圖,菱形ABCD的邊長為4,E,F分別是AB,AD邊上的動點,BE=AF,∠BAD=120°,則下列結(jié)論:①△BEC≌△AFC;②△ECF為等邊三角形;③∠AGE=∠AFC;④若AF=1,則![]() . 其中正確結(jié)論的序號有________.
. 其中正確結(jié)論的序號有________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
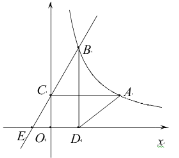
【題目】如圖,已知反比例函數(shù)![]() 的圖象經(jīng)過點
的圖象經(jīng)過點![]() ,過
,過![]() 作
作![]() 軸于點
軸于點![]() .點
.點![]() 為反比例函數(shù)圖象上的一動點,過點
為反比例函數(shù)圖象上的一動點,過點![]() 作
作![]() 軸于點
軸于點![]() ,連接
,連接![]() .直線
.直線![]() 與
與![]() 軸的負(fù)半軸交于點
軸的負(fù)半軸交于點![]() .
.
(1)求反比例函數(shù)的表達(dá)式;
(2)若![]() ,求
,求![]() 的面積;
的面積;
(3)是否存在點![]() ,使得四邊形
,使得四邊形![]() 為平行四邊形?若存在,請求出點
為平行四邊形?若存在,請求出點![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com